- 数学Ⅱ|図形と方程式「円と直線との共有点の条件と点と直線との距離」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|円と直線との共有点の条件と点と直線との距離
図形と方程式 41円 \(x^2+y^2=5\) と直線 \(x-3y+k=0\) の共有点の個数は定数 \(k\) によってどのように変化するか、点と直線との距離を用いて調べる方法は?
高校数学Ⅱ|図形と方程式
解法のPoint
円と直線との共有点の条件と点と直線との距離
Point:円と直線との共有点の条件と点と直線との距離
① 円の方程式より、中心の座標と半径 \(r\) を求める。
中心 \((0~,~0)\)、半径 \(r=\sqrt{5}\)
② 中心と直線との距離 \(d\) を公式より求める。
\(d=\displaystyle \frac{\,|\,0-3 \cdot 0+k\,|\,}{\,\sqrt{1^2+(-3)^2}\,}=\displaystyle \frac{\,|\,k\,|\,}{\,\sqrt{10}\,}\)
③ 距離 \(d\) と半径 \(r\) の大小関係より、共有点の個数の条件を調べる。

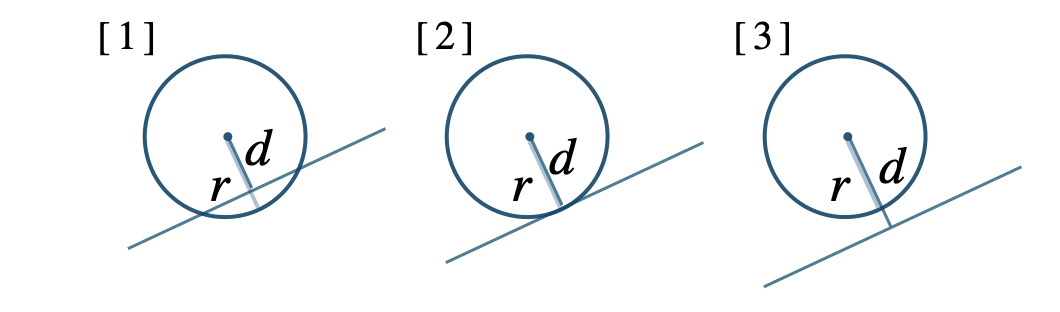
\({\small [\,1\,]}~\)\(d \lt r\) のとき、共有点 \(2\) 個
\({\small [\,2\,]}~\)\(d=r\) のとき、共有点 \(1\) 個
\({\small [\,3\,]}~\)\(d \gt r\) のとき、共有点 \(0\) 個
点と直線との距離の公式を用いた円と直線との共有点の個数の条件は、
① 円の方程式より、中心の座標と半径 \(r\) を求める。
中心 \((0~,~0)\)、半径 \(r=\sqrt{5}\)
② 中心と直線との距離 \(d\) を公式より求める。
\(d=\displaystyle \frac{\,|\,0-3 \cdot 0+k\,|\,}{\,\sqrt{1^2+(-3)^2}\,}=\displaystyle \frac{\,|\,k\,|\,}{\,\sqrt{10}\,}\)
③ 距離 \(d\) と半径 \(r\) の大小関係より、共有点の個数の条件を調べる。
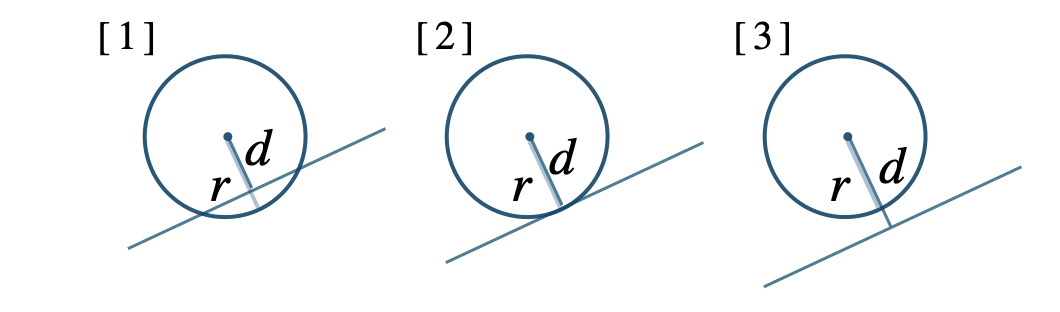
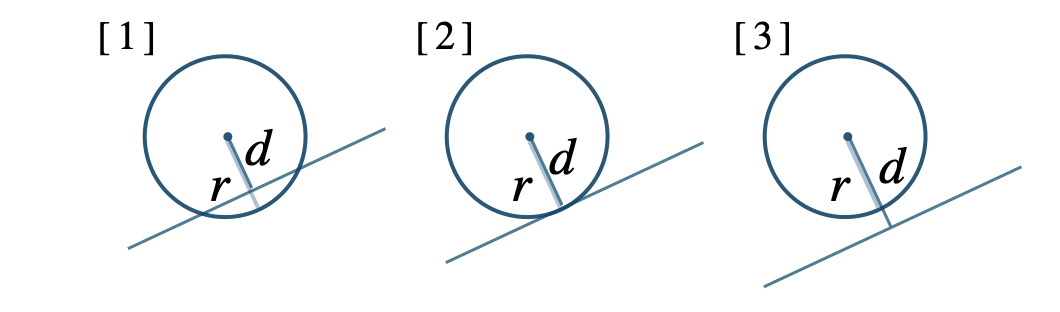
\({\small [\,1\,]}~\)\(d \lt r\) のとき、共有点 \(2\) 個
\({\small [\,2\,]}~\)\(d=r\) のとき、共有点 \(1\) 個
\({\small [\,3\,]}~\)\(d \gt r\) のとき、共有点 \(0\) 個
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|円と直線との共有点の条件と点と直線との距離
図形と方程式 41
円 \(x^2+y^2=5\) と直線 \(x-3y+k=0\) の共有点の個数は定数 \(k\) によってどのように変化するか、点と直線との距離を用いて調べる方法は?
高校数学Ⅱ|図形と方程式
円 \(x^2+y^2=5\) は、中心 \((0~,~0)\)、半径 \(r=\sqrt{5}\) の円となる
ここで、中心 \((0~,~0)\) と直線 \(x-3y+k=0\) との距離 \(d\) は、
\(\begin{eqnarray}~~~d&=&\displaystyle \frac{\,|\,0-3 \cdot 0+k\,|\,}{\,\sqrt{1^2+(-3)^2}\,}
\\[5pt]~~~&=&\displaystyle \frac{\,|\,k\,|\,}{\,\sqrt{1+9}\,}
\\[5pt]~~~&=&\displaystyle \frac{\,|\,k\,|\,}{\,\sqrt{10}\,}\end{eqnarray}\)
\({\small (\,1\,)}~\)\(d \lt r\) のとき、
\(\begin{eqnarray}~~~\displaystyle \frac{\,|\,k\,|\,}{\,\sqrt{10}\,}&\lt&\sqrt{5}
\\[5pt]~~~|\,k\,|&\lt&\sqrt{5} \cdot \sqrt{10}
\\[3pt]~~~|\,k\,|&\lt&5\sqrt{2}\end{eqnarray}\)
よって、\(-5\sqrt{2} \lt k \lt 5\sqrt{2}\) のとき、共有点 \(2\) 個
\({\small (\,2\,)}~\)\(d=r\) のとき、
\(\begin{eqnarray}~~~\displaystyle \frac{\,|\,k\,|\,}{\,\sqrt{10}\,}&=&\sqrt{5}
\\[5pt]~~~|\,k\,|&=&\sqrt{5} \cdot \sqrt{10}
\\[3pt]~~~|\,k\,|&=&5\sqrt{2}\end{eqnarray}\)
よって、\(k=\pm 5\sqrt{2}\) のとき、共有点 \(1\) 個
\({\small (\,3\,)}~\)\(d \gt r\) のとき、
\(\begin{eqnarray}~~~\displaystyle \frac{\,|\,k\,|\,}{\,\sqrt{10}\,}&\gt&\sqrt{5}
\\[5pt]~~~|\,k\,|&\gt&\sqrt{5} \cdot \sqrt{10}
\\[3pt]~~~|\,k\,|&\gt&5\sqrt{2}\end{eqnarray}\)
よって、\(k \lt -5\sqrt{2}~,~5\sqrt{2} \lt k\) のとき、共有点 \(0\) 個
したがって、
\(-5\sqrt{2} \lt k \lt 5\sqrt{2}\) のとき共有点 \(2\) 個
\(k=\pm 5\sqrt{2}\) のとき共有点 \(1\) 個
\(k \lt -5\sqrt{2}~,~5\sqrt{2} \lt k\) のとき共有点 \(0\) 個



