- 数学Ⅱ|図形と方程式「直線が円によって切り取られる線分」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|直線が円によって切り取られる線分
図形と方程式 42直線 \(y=x+1\) が円 \(x^2+y^2=5\) によって切り取られる線分の長さの求め方は?
高校数学Ⅱ|図形と方程式
解法のPoint
直線が円によって切り取られる線分
Point:直線が円によって切り取られる線分
① 円の中心の座標と半径 \(r\) を求める。
中心 \((0~,~0)\)、半径 \(r=\sqrt{5}\)
② 円の中心と直線との距離 \(d\) を求める。
\(d=\displaystyle \frac{\,|\,0-0+1\,|\,}{\,\sqrt{1^2+(-1)^2}\,}=\displaystyle \frac{\,1\,}{\,\sqrt{2}\,}\)
③ 弦の長さの半分の \(\displaystyle \frac{\,\ell\,}{\,2\,}\) と半径 \(r\)、距離 \(d\) で直角三角形ができるので、三平方の定理を用いて \(\ell\) を求める。

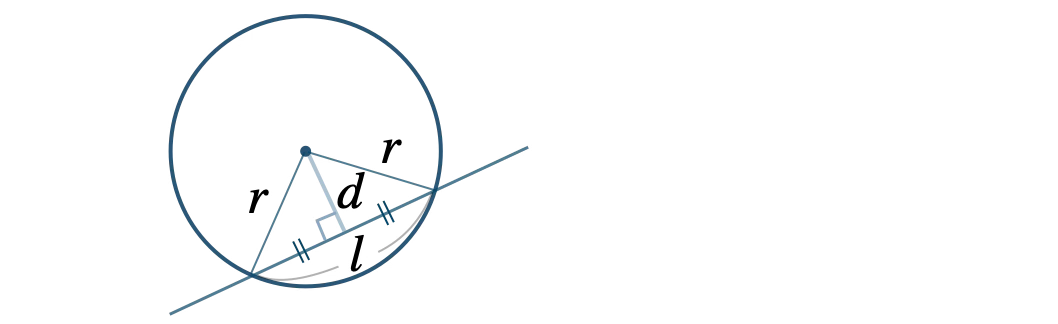
\(\left(\displaystyle \frac{\,\ell\,}{\,2\,}\right)^2+d^2=r^2\)
直線が円によって切り取られる弦の長さは、
① 円の中心の座標と半径 \(r\) を求める。
中心 \((0~,~0)\)、半径 \(r=\sqrt{5}\)
② 円の中心と直線との距離 \(d\) を求める。
\(d=\displaystyle \frac{\,|\,0-0+1\,|\,}{\,\sqrt{1^2+(-1)^2}\,}=\displaystyle \frac{\,1\,}{\,\sqrt{2}\,}\)
③ 弦の長さの半分の \(\displaystyle \frac{\,\ell\,}{\,2\,}\) と半径 \(r\)、距離 \(d\) で直角三角形ができるので、三平方の定理を用いて \(\ell\) を求める。


\(\left(\displaystyle \frac{\,\ell\,}{\,2\,}\right)^2+d^2=r^2\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|直線が円によって切り取られる線分
図形と方程式 42
直線 \(y=x+1\) が円 \(x^2+y^2=5\) によって切り取られる線分の長さの求め方は?
高校数学Ⅱ|図形と方程式
この弦の長さを \(\ell\) とおく
円 \(x^2+y^2=5\) は、中心 \((0~,~0)\)、半径 \(r=\sqrt{5}\) である
直線 \(y=x+1~\Leftrightarrow~x-y+1=0\) と中心 \((0~,~0)\) との距離 \(d\) は、
\(\begin{eqnarray}~~~d&=&\displaystyle \frac{\,|\,0-0+1\,|\,}{\,\sqrt{1^2+(-1)^2}\,}
\\[5pt]~~~&=&\displaystyle \frac{\,|\,1\,|\,}{\,\sqrt{1+1}\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,\sqrt{2}\,}\end{eqnarray}\)
ここで、\(d\) は弦に垂直に交わり、弦 \(\ell\) を2等分するので、半径 \(r=\sqrt{5}\) を斜辺とした三平方の定理より、
\(\begin{eqnarray}~~~\left(\displaystyle \frac{\,\ell\,}{\,2\,}\right)^2+d^2&=&r^2
\\[5pt]~~~\displaystyle \frac{\,\ell^2\,}{\,4\,}+\left(\displaystyle \frac{\,1\,}{\,\sqrt{2}\,}\right)^2&=&\left(\sqrt{5}\right)^2
\\[5pt]~~~\displaystyle \frac{\,\ell^2\,}{\,4\,}+\displaystyle \frac{\,1\,}{\,2\,}&=&5
\\[5pt]~~~\ell^2+2&=&20~~~\hspace{10pt}(\,∵~{\small \times}~4\,)
\\[3pt]~~~\ell^2&=&18
\\[3pt]~~~\ell&=&\sqrt{18}~~~\hspace{10pt}(\,∵~\ell \gt 0\,)
\\[3pt]~~~\ell&=&3\sqrt{2}\end{eqnarray}\)
したがって、弦の長さは \(3\sqrt{2}\) となる



