- 数学Ⅱ|図形と方程式「外部の点から円に引いた接線の方程式」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|外部の点から円に引いた接線の方程式
図形と方程式 45点 \((3~,~1)\) を通り、円 \(x^2+y^2=5\) に接する直線の方程式の求め方は?
高校数学Ⅱ|図形と方程式
解法のPoint
外部の点から円に引いた接線の方程式
Point:外部の点から円に引いた接線の方程式
① 接点の座標を \((a~,~b)\) とおく。
② 接点が円上にある条件式をつくる。
\(x^2+y^2=5\) より、
\(a^2+b^2=5~~~\cdots {\small [\,1\,]}\)
③ 接線の方程式を \(a~,~b\) を用いて表す。
\(ax+by=5~~~\cdots {\small [\,2\,]}\)
④ 外部の点を代入して条件式をつくる。
\(3a+b=5~~~\cdots {\small [\,3\,]}\)
⑤ \({\small [\,1\,]}\) と \({\small [\,3\,]}\) を連立して \(a~,~b\) の値を求め、\({\small [\,2\,]}\) より接線の方程式を求める。
外部の点から円に引いた接線の方程式の求め方は、
① 接点の座標を \((a~,~b)\) とおく。
② 接点が円上にある条件式をつくる。
\(x^2+y^2=5\) より、
\(a^2+b^2=5~~~\cdots {\small [\,1\,]}\)
③ 接線の方程式を \(a~,~b\) を用いて表す。
\(ax+by=5~~~\cdots {\small [\,2\,]}\)
④ 外部の点を代入して条件式をつくる。
\(3a+b=5~~~\cdots {\small [\,3\,]}\)
⑤ \({\small [\,1\,]}\) と \({\small [\,3\,]}\) を連立して \(a~,~b\) の値を求め、\({\small [\,2\,]}\) より接線の方程式を求める。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|外部の点から円に引いた接線の方程式
図形と方程式 45
点 \((3~,~1)\) を通り、円 \(x^2+y^2=5\) に接する直線の方程式の求め方は?
高校数学Ⅱ|図形と方程式
この円の接線の、接点の座標を \((a~,~b)\) とおくと、
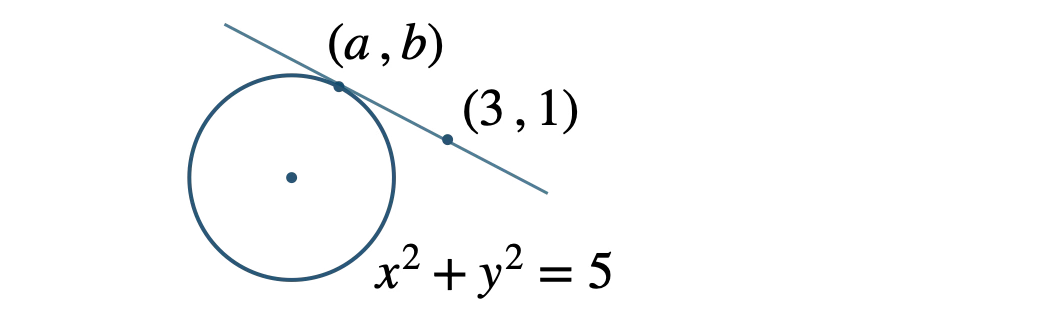

接点が円上にあるので、
\(a^2+b^2=5~~~\cdots {\small [\,1\,]}\)
また、接線の方程式は、
円の方程式を \(x \cdot x+y \cdot y=5\) とし、接点 \((x~,~y)=(a~,~b)\) を代入すると、
\(ax+by=5~~~\cdots {\small [\,2\,]}\)
この接線が点 \((3~,~1)\) を通るので、
\(\begin{eqnarray}~~~a \cdot 3+b \cdot 1&=&5
\\[3pt]~~~3a+b&=&5
\\[3pt]~~~b&=&-3a+5~~~\cdots {\small [\,3\,]}\end{eqnarray}\)
次に、\({\small [\,3\,]}\) を \({\small [\,1\,]}\) に代入すると、
\(\begin{eqnarray}~~~a^2+(-3a+5)^2&=&5
\\[3pt]~~~a^2+(9a^2-30a+25)-5&=&0
\\[3pt]~~~10a^2-30a+20&=&0
\\[3pt]~~~a^2-3a+2&=&0
\\[3pt]~~~(a-1)(a-2)&=&0
\\[3pt]~~~a&=&1~,~2\end{eqnarray}\)
\(a=1\) のとき、\({\small [\,3\,]}\) より、
\(\begin{eqnarray}~~~b&=&-3 \cdot 1+5
\\[3pt]~~~&=&-3+5
\\[3pt]~~~&=&2\end{eqnarray}\)
\({\small [\,2\,]}\) に代入すると、
\(\begin{eqnarray}~~~1 \cdot x+2 \cdot y&=&5
\\[3pt]~~~x+2y&=&5\end{eqnarray}\)
\(a=2\) のとき、\({\small [\,3\,]}\) より、
\(\begin{eqnarray}~~~b&=&-3 \cdot 2+5
\\[3pt]~~~&=&-6+5
\\[3pt]~~~&=&-1\end{eqnarray}\)
\({\small [\,2\,]}\) に代入すると、
\(\begin{eqnarray}~~~2 \cdot x+(-1) \cdot y&=&5
\\[3pt]~~~2x-y&=&5\end{eqnarray}\)
したがって、
接線の方程式は \(x+2y=5\) 、\(2x-y=5\)



