- 数学Ⅱ|図形と方程式「(x-a)²+(y-b)²=r²上の点における接線の方程式」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
目次
問題|(x-a)²+(y-b)²=r²上の点における接線の方程式
図形と方程式 49☆円 \((x-2)^2+(y+3)^2=5\) 上の点 \((3~,~-1)\) における接線の方程式の求め方は?
高校数学Ⅱ|図形と方程式
解法のPoint
(x-a)²+(y-b)²=r²上の点における接線の方程式
Point:(x-a)²+(y-b)²=r²上の点における接線の方程式
① 円の中心と円上の点を結ぶ直線の傾きを求める。
\((2~,~-3)\) と \((3~,~-1)\) より、傾き \(2\)
② 接線は①の直線と垂直に交わるので、傾きの積が \(-1\) より、接線の傾きを求める。
\(2 \cdot m=-1~~\Leftrightarrow~~m=-\displaystyle\frac{\,1\,}{\,2\,}\)
③ 傾きと接点の座標より、接線の方程式を求める。
\(\begin{eqnarray}y-(-1)&=&-\displaystyle\frac{\,1\,}{\,2\,}(x-3)
\\[3pt]\Leftrightarrow~~~x+2y-1&=&0\end{eqnarray}\)
円 \((x-2)^2+(y+3)^2=5\) 上の点 \((3~,~-1)\) における接線の求め方は、
① 円の中心と円上の点を結ぶ直線の傾きを求める。
\((2~,~-3)\) と \((3~,~-1)\) より、傾き \(2\)
② 接線は①の直線と垂直に交わるので、傾きの積が \(-1\) より、接線の傾きを求める。
\(2 \cdot m=-1~~\Leftrightarrow~~m=-\displaystyle\frac{\,1\,}{\,2\,}\)
③ 傾きと接点の座標より、接線の方程式を求める。
\(\begin{eqnarray}y-(-1)&=&-\displaystyle\frac{\,1\,}{\,2\,}(x-3)
\\[3pt]\Leftrightarrow~~~x+2y-1&=&0\end{eqnarray}\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|(x-a)²+(y-b)²=r²上の点における接線の方程式
図形と方程式 49☆
円 \((x-2)^2+(y+3)^2=5\) 上の点 \((3~,~-1)\) における接線の方程式の求め方は?
高校数学Ⅱ|図形と方程式
円 \((x-2)^2+(y+3)^2=5\) は、
中心 \((2~,~-3)\)、半径 \(\sqrt{5}\) の円
2点 \((2~,~-3)\)、\((3~,~-1)\) を結ぶ直線の傾きは、
下の図は実際の座標の位置関係とは異なるが、計算の手順を統一するために、常にこの形で図を描くとよい。

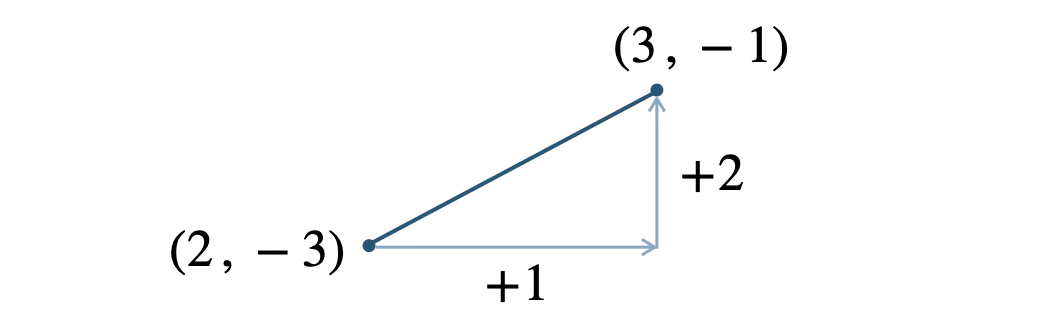


\(x\) の増加量が \(3-2=+1\)
\(y\) の増加量が \(-1-(-3)=+2\)
よって、\(\displaystyle\frac{\,+2\,}{\,+1\,}=2\) となる
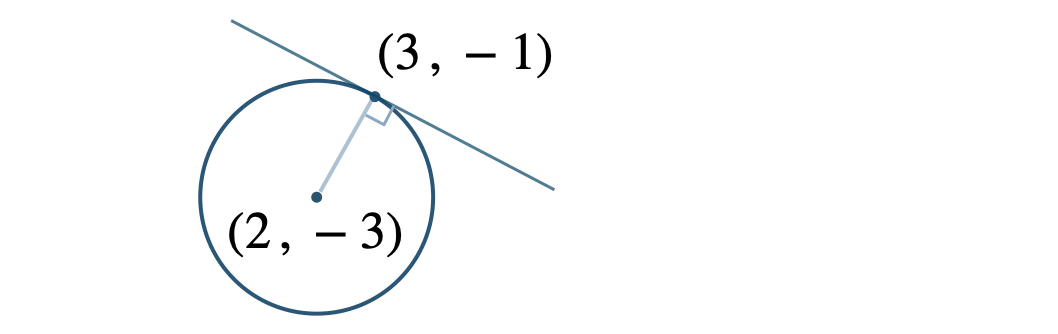

接線の傾きを \(m\) とすると、垂直に交わるので、傾きの積が \(-1\) より、
\(\begin{eqnarray}~~~2 \cdot m&=&-1
\\[3pt]~~~m&=&-\displaystyle\frac{\,1\,}{\,2\,}\end{eqnarray}\)
これより、接線は点 \((3~,~-1)\) を通り傾き \(\displaystyle -\frac{\,1\,}{\,2\,}\) であるので、
\(\begin{eqnarray}~~~y-(-1)&=&-\displaystyle\frac{\,1\,}{\,2\,}(x-3)
\\[3pt]~~~2(y+1)&=&-(x-3)~~~\hspace{10pt}(\,∵~\times 2\,)
\\[3pt]~~~2y+2&=&-x+3
\\[3pt]~~~x+2y+2-3&=&0
\\[3pt]~~~x+2y-1&=&0\end{eqnarray}\)
したがって、接線の方程式は \(x+2y-1=0\)
【別解】
円 \((x-2)^2+(y+3)^2=5\) を
\((x-2)(x-2)+(y+3)(y+3)=5\) として、
一方の \((x-2)\) と \((y+3)\) に点 \((3~,~-1)\) を代入すると、
\(\begin{eqnarray}~~~(3-2)(x-2)+(-1+3)(y+3)&=&5
\\[3pt]~~~(x-2)+2(y+3)&=&5
\\[3pt]~~~x-2+2y+6-5&=&0
\\[3pt]~~~x+2y-1&=&\end{eqnarray}\)
したがって、接線の方程式は \(x+2y-1=0\)



