- 数学Ⅱ|図形と方程式「2つの円の位置関係」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|2つの円の位置関係
図形と方程式 51円 \(x^2+y^2=9\) と円 \((x-4)^2+(y-3)^2=16\) の位置関係の調べ方は?
高校数学Ⅱ|図形と方程式
解法のPoint
2つの円の位置関係
Point:2つの円の位置関係
① 2つの円の中心の座標と半径を求める。
② 2つの円の中心間の距離 \(d\) を求める。
③ 2つの円の半径 \(r\)、\(r’\) の和と差を求める。
和は \(r+r’\)、差は \(|\,r-r’\,|\)
④ 半径の和・差と距離 \(d\) の大小関係より、2つの円の位置関係を定める。

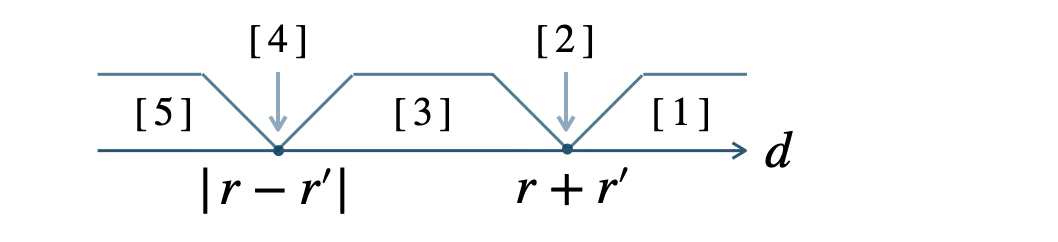
\({\small [\,1\,]}\) \(d \gt r+r’\) のとき、互いに外部にある
\({\small [\,2\,]}\) \(d=r+r’\) のとき、外接する
\({\small [\,3\,]}\) \(|\,r-r’\,| \lt d \lt r+r’\) のとき、2点で交わる
\({\small [\,4\,]}\) \(d=|\,r-r’\,|\) のとき、内接する
\({\small [\,5\,]}\) \(d \lt |\,r-r’\,|\) のとき、一方が他方の内部にある

2つの円の位置関係の調べ方は、
① 2つの円の中心の座標と半径を求める。
② 2つの円の中心間の距離 \(d\) を求める。
③ 2つの円の半径 \(r\)、\(r’\) の和と差を求める。
和は \(r+r’\)、差は \(|\,r-r’\,|\)
④ 半径の和・差と距離 \(d\) の大小関係より、2つの円の位置関係を定める。


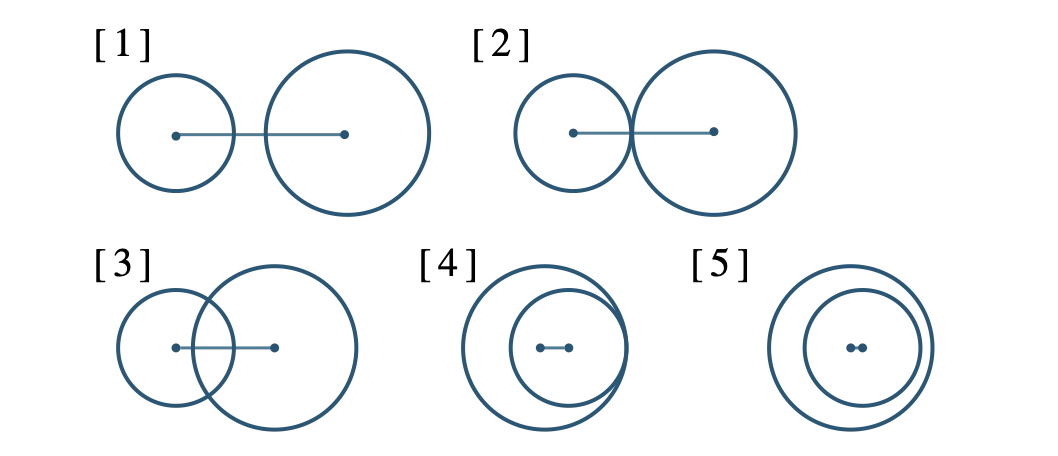
\({\small [\,1\,]}\) \(d \gt r+r’\) のとき、互いに外部にある
\({\small [\,2\,]}\) \(d=r+r’\) のとき、外接する
\({\small [\,3\,]}\) \(|\,r-r’\,| \lt d \lt r+r’\) のとき、2点で交わる
\({\small [\,4\,]}\) \(d=|\,r-r’\,|\) のとき、内接する
\({\small [\,5\,]}\) \(d \lt |\,r-r’\,|\) のとき、一方が他方の内部にある


©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|2つの円の位置関係
図形と方程式 51
円 \(x^2+y^2=9\) と円 \((x-4)^2+(y-3)^2=16\) の位置関係の調べ方は?
高校数学Ⅱ|図形と方程式
円 \(x^2+y^2=9\) は、
中心 \((0~,~0)\)、半径 \(3\) の円
円 \((x-4)^2+(y-3)^2=16\) は、
中心 \((4~,~3)\)、半径 \(4\) の円
2つの円の中心間の距離 \(d\) は、
\(\begin{eqnarray}~~~d&=&\sqrt{4^2+3^2}
\\[3pt]~~~&=&\sqrt{16+9}
\\[3pt]~~~&=&\sqrt{25}
\\[3pt]~~~&=&5\end{eqnarray}\)
次に、2つの円の半径の和と差は、
和が \(3+4=7\)
差が \(|\,3-4\,|=1\)
中心間の距離 \(d\) は、\(1 \lt d \lt 7\) を満たす
したがって、2つの円は2点で交わる



