- 数学Ⅱ|図形と方程式「連立不等式の領域の図の読み取り」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|連立不等式の領域の図の読み取り
図形と方程式 64☆次の連立不等式の表す領域の図から連立不等式を求める方法は?


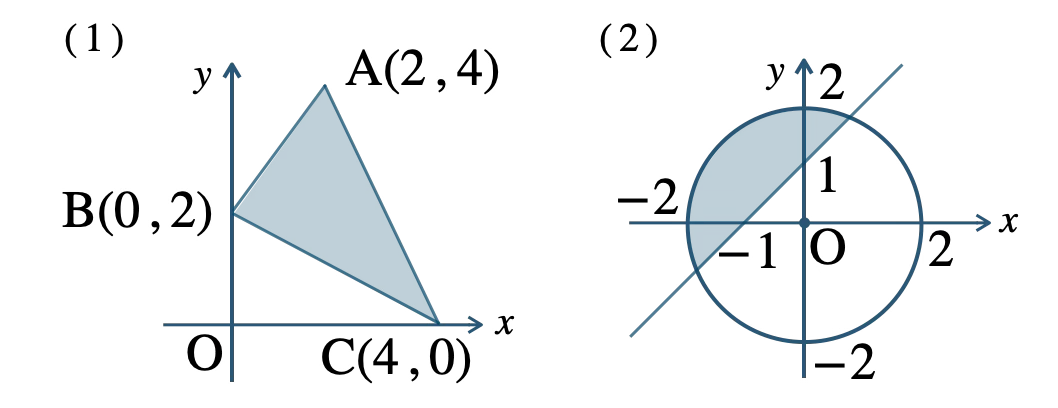
\({\small (1)}~\)は境界線を含まない
\({\small (2)}~\)は境界線を含む



\({\small (1)}~\)は境界線を含まない
\({\small (2)}~\)は境界線を含む
高校数学Ⅱ|図形と方程式
解法のPoint
連立不等式の領域の図の読み取り
Point:連立不等式の領域の図の読み取り
① すべての境界線の方程式を求める。
② 直線では上側or下側を、円では内側or外側を読み取り、境界線を含む場合は不等号にイコールをつける。
\({\small [\,1\,]}\) 直線の上側は \(y{\small ~≧~}ax+b\)
\({\small [\,2\,]}\) 直線の下側は \(y{\small ~≦~}ax+b\)
\({\small [\,3\,]}\) 円の内側は \(x^2+y^2{\small ~≦~}r^2\)
\({\small [\,4\,]}\) 円の外側は \(x^2+y^2{\small ~≧~}r^2\)
③ これより、連立不等式を求める。
連立不等式の表す領域の図から連立不等式を求めるには、
① すべての境界線の方程式を求める。
② 直線では上側or下側を、円では内側or外側を読み取り、境界線を含む場合は不等号にイコールをつける。
\({\small [\,1\,]}\) 直線の上側は \(y{\small ~≧~}ax+b\)
\({\small [\,2\,]}\) 直線の下側は \(y{\small ~≦~}ax+b\)
\({\small [\,3\,]}\) 円の内側は \(x^2+y^2{\small ~≦~}r^2\)
\({\small [\,4\,]}\) 円の外側は \(x^2+y^2{\small ~≧~}r^2\)
③ これより、連立不等式を求める。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|連立不等式の領域の図の読み取り
図形と方程式 64☆
次の連立不等式の表す領域の図から連立不等式を求める方法は?

\({\small (1)}~\)は境界線を含まない
\({\small (2)}~\)は境界線を含む
高校数学Ⅱ|図形と方程式
\({\small (1)}~\)
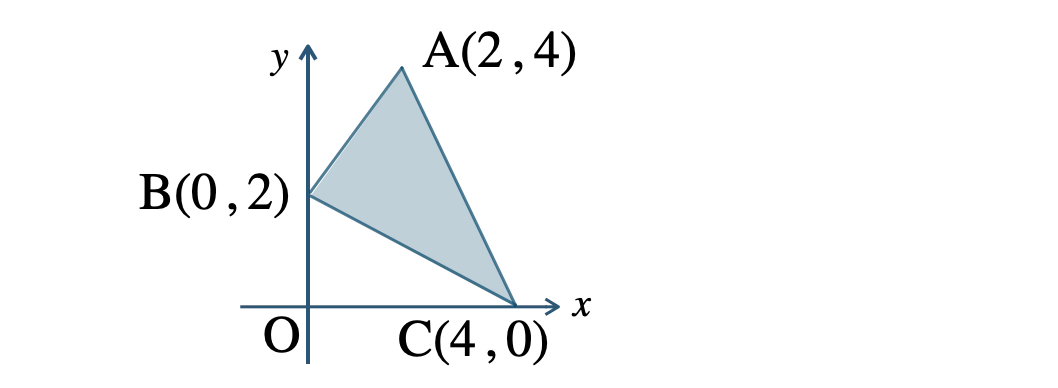
直線 \({\rm AB}\) の傾きは、
\(\displaystyle \frac{\,4-2\,}{\,2-0\,}=2\)
\(y\) 切片が \(2\) より、
\(y=2x+2\)
直線 \({\rm BC}\) の傾きは、
\(\displaystyle \frac{\,0-2\,}{\,4-0\,}=-\displaystyle \frac{\,1\,}{\,2\,}\)
\(y\) 切片が \(2\) より、
\(y=-\displaystyle \frac{\,1\,}{\,2\,}x+2\)
直線 \({\rm AC}\) の傾きは、
\(\displaystyle \frac{\,0-4\,}{\,4-2\,}=\displaystyle \frac{\,-4\,}{\,2\,}=-2\)
点 \((4~,~0)\) を通るので、
\(\begin{eqnarray}~~~y-0&=&-2(x-4)\\[3pt]~~~y&=&-2x+8\end{eqnarray}\)
よって、領域は、
直線 \({\rm AB}\) の下側 かつ
直線 \({\rm BC}\) の上側 かつ
直線 \({\rm AC}\) の下側
となり、この領域の連立不等式は、
\(\left\{~\begin{array}{l}y \lt 2x+2\\y \gt -\displaystyle \frac{\,1\,}{\,2\,}x+2\\y \lt -2x+8\end{array}\right.\)
\({\small (2)}~\)

直線の境界線は、傾きが \(1\)、\(y\) 切片が \(1\) であるので、
直線\(y=x+1\)の上側
円の境界線は、中心 \((0~,~0)\)、半径 \(2\) であるので、
円 \(x^2+y^2=2^2\) の内部
また、境界線を含むので、この領域の連立不等式は、
\(\left\{~\begin{array}{l}y{\small ~≧~}x+1\\x^2+y^2{\small ~≦~}4\end{array}\right.\)



