- 数学Ⅱ|図形と方程式「放物線が境界線の不等式の領域」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|放物線が境界線の不等式の領域
図形と方程式 65☆不等式 \(y \gt x^2+1\)、\(y {\small ~≦~} x^2-4x\) の表す領域の図示の方法は?
高校数学Ⅱ|図形と方程式
解法のPoint
放物線が境界線の不等式の領域
Point:放物線が境界線の不等式の領域
① 標準形に変形し、放物線の頂点を求める。
② 放物線を図示し、yが大きいときは上側、yが小さいときは下側が領域となる。
\({\small [\,1\,]}~y {\small ~≧~} a(x-p)^2+q\) は放物線の上側
\({\small [\,2\,]}~y {\small ~≦~} a(x-p)^2+q\) は放物線の下側

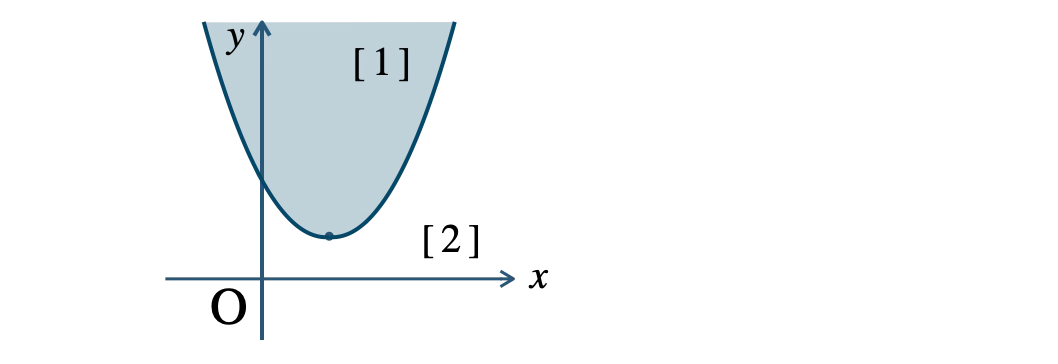
③ 境界線を含むか含まないかを判別する。
不等号にイコールを、
含む \({\small ~≦~}~,~{\small ~≧~}\) \(\Rightarrow\) 境界線を含む
含まない \(\lt~,~\gt\) \(\Rightarrow\) 境界線を含まない
放物線が境界線の不等式の領域は、
① 標準形に変形し、放物線の頂点を求める。
② 放物線を図示し、yが大きいときは上側、yが小さいときは下側が領域となる。
\({\small [\,1\,]}~y {\small ~≧~} a(x-p)^2+q\) は放物線の上側
\({\small [\,2\,]}~y {\small ~≦~} a(x-p)^2+q\) は放物線の下側


③ 境界線を含むか含まないかを判別する。
不等号にイコールを、
含む \({\small ~≦~}~,~{\small ~≧~}\) \(\Rightarrow\) 境界線を含む
含まない \(\lt~,~\gt\) \(\Rightarrow\) 境界線を含まない
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|放物線が境界線の不等式の領域
図形と方程式 65☆
不等式 \(y \gt x^2+1\)、\(y {\small ~≦~} x^2-4x\) の表す領域の図示の方法は?
高校数学Ⅱ|図形と方程式
\(y=x^2+1\) は頂点 \((0~,~1)\) で下に凸の放物線で、
\(y \gt x^2+1\) はこの放物線の上側となる


ただし、境界線を含まない
\(y {\small ~≦~} x^2-4x\) は、
\(\begin{eqnarray}~~~y&{\small ~≦~}&(x^2-4x+4)-4\\[3pt]~~~y&{\small ~≦~}&(x-2)^2-4\end{eqnarray}\)
よって、頂点 \((2~,~-4)\) で下に凸の放物線の下側となる
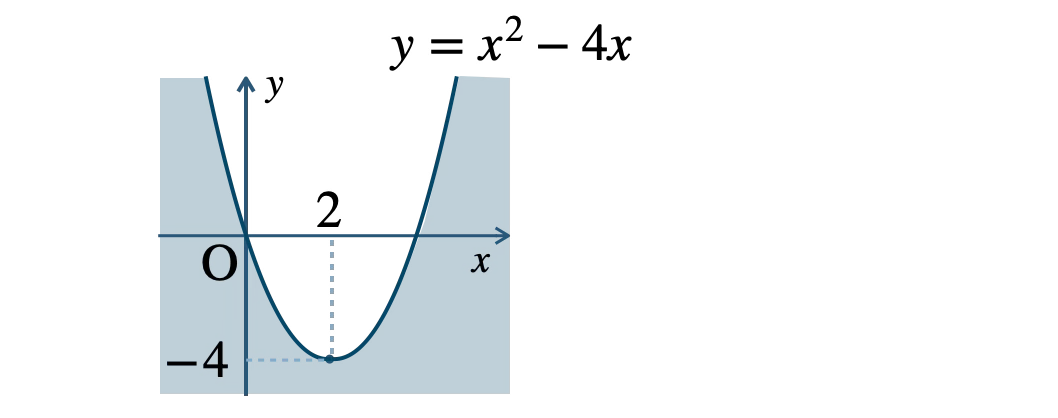

ただし、境界線を含む



