- 数学Ⅱ|図形と方程式「領域を用いた証明」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|領域を用いた証明
図形と方程式 68\(x~,~y\) が実数のとき、\(x^2+y^2 \lt 1\) ならば \(x^2+y^2-2x-3 \lt 0\) の証明方法は?
高校数学Ⅱ|図形と方程式
解法のPoint
領域を用いた証明
Point:領域を用いた証明
① 命題の不等式の領域 \({\rm P}\)、\({\rm Q}\) を図示する。
② 図より、\({\rm P} \subset {\rm Q}\)( \({\rm P}\) が \({\rm Q}\) の部分集合 )であることより、命題を証明する。
\({\rm P} \subset {\rm Q}\) であれば、\({\rm P}\) ならば \({\rm Q}\) が成り立つ。
不等式の領域を用いた証明は、
① 命題の不等式の領域 \({\rm P}\)、\({\rm Q}\) を図示する。
② 図より、\({\rm P} \subset {\rm Q}\)( \({\rm P}\) が \({\rm Q}\) の部分集合 )であることより、命題を証明する。
\({\rm P} \subset {\rm Q}\) であれば、\({\rm P}\) ならば \({\rm Q}\) が成り立つ。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|領域を用いた証明
図形と方程式 68
\(x~,~y\) が実数のとき、\(x^2+y^2 \lt 1\) ならば \(x^2+y^2-2x-3 \lt 0\) の証明方法は?
高校数学Ⅱ|図形と方程式
[証明] 不等式 \(x^2+y^2 \lt 1\) は、
中心 \((0~,~0)\)、半径 \(1\) の円の内部で、この領域を \({\rm P}\) とする
不等式 \(x^2+y^2-2x-3 \lt 0\) は、\(x\) について、平方完成すると、
\(\begin{eqnarray}~~~(x^2-2x)+y^2-3&\lt&0
\\[3pt]~~~(x^2-2x+1)-1+y^2-3&\lt&0
\\[3pt]~~~(x-1)^2+y^2&\lt&4\end{eqnarray}\)
よって、中心 \((1~,~0)\)、半径 \(2\) の円の内部で、この領域を \({\rm Q}\) とする
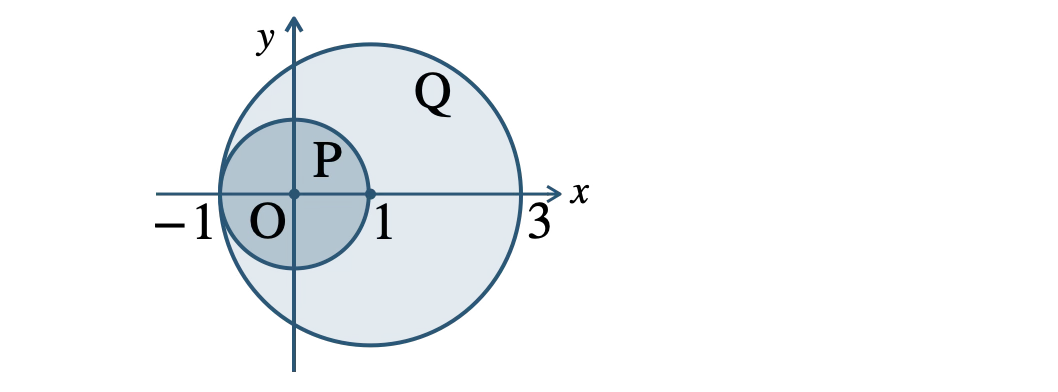

図より、\({\rm P} \subset {\rm Q}\)( \({\rm P}\) が \({\rm Q}\) の部分集合 )であるから、
\(x^2+y^2 \lt 1\) ならば \(x^2+y^2-2x-3 \lt 0\) である [終]



