このページは、「領域を用いた証明」の練習問題アーカイブページとなります。
この問題の解き方の詳細は↓
領域を用いた証明 で確認できます。
問題アーカイブ01
問題アーカイブ01\(x~,~y\) が実数のとき、\(x^2+y^2 \lt 1\) ならば \(x+y \lt \sqrt{\,2\,}\) を証明せよ。
数研出版|数学Ⅱ[709] p.117 練習48
[証明] 不等式 \(x^2+y^2 \lt 1\) は、
中心 \((0~,~0)\)、半径 \(1\) の円の内部で、この領域を \({\rm P}\) とする
不等式 \(x+y \lt \sqrt{\,2\,}\) は、
\(\begin{eqnarray}~~~x+y&\lt&\sqrt{\,2\,}
\\[3pt]~~~y&\lt&-x+\sqrt{\,2\,}\end{eqnarray}\)
直線 \(y=-x+\sqrt{\,2\,}\) の下側の領域で、この領域を \({\rm Q}\) とする
また、直線 \(x+y-\sqrt{\,2\,}=0\) と原点 \((0~,~0)\) との距離 \(d\) は、
\(\begin{eqnarray}~~~d&=&\displaystyle \frac{\,|\,0+0-\sqrt{\,2\,}\,|\,}{\,\sqrt{1^2+1^2}\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\sqrt{\,2\,}\,}{\,\sqrt{\,2\,}\,}=1\end{eqnarray}\)
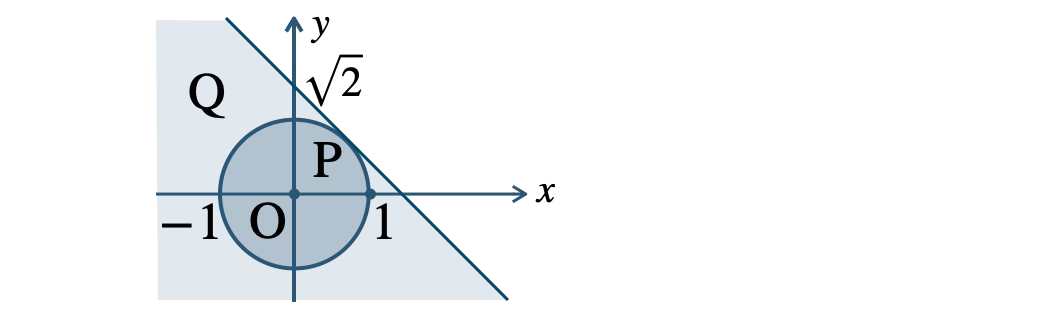
図より、\({\rm P} \subset {\rm Q}\)( \({\rm P}\) が \({\rm Q}\) の部分集合 )であるから、
\(x^2+y^2 \lt 1\) ならば \(x+y \lt \sqrt{\,2\,}\) である [終]
問題アーカイブ02
問題アーカイブ02\(x~,~y\) が実数のとき、\(x^2+y^2 {\small ~≦~} 1\) ならば \(x+y {\small ~≦~} \sqrt{\,2\,}\) を証明せよ。
数研出版|高等学校数学Ⅱ[710] p.108 練習42
数研出版|新編数学Ⅱ[711] p.107 補充問題 11
[証明] 不等式 \(x^2+y^2 {\small ~≦~} 1\) は、
中心 \((0~,~0)\)、半径 \(1\) の円の内部および周上で、この領域を \({\rm P}\) とする
不等式 \(x+y {\small ~≦~} \sqrt{\,2\,}\) は、
\(\begin{eqnarray}~~~x+y&{\small ~≦~}&\sqrt{\,2\,}
\\[3pt]~~~y&{\small ~≦~}&-x+\sqrt{\,2\,}\end{eqnarray}\)
直線 \(y=-x+\sqrt{\,2\,}\) の下側および直線上の領域で、この領域を \({\rm Q}\) とする
また、直線 \(x+y-\sqrt{\,2\,}=0\) と原点 \((0~,~0)\) との距離 \(d\) は、
\(\begin{eqnarray}~~~d&=&\displaystyle \frac{\,|\,0+0-\sqrt{\,2\,}\,|\,}{\,\sqrt{\,1^2+1^2\,}\,}
\\[5pt]~~~&=&\displaystyle \frac{\,\sqrt{\,2\,}\,}{\,\sqrt{\,2\,}\,}=1\end{eqnarray}\)



図より、\({\rm P} \subset {\rm Q}\)( \({\rm P}\) が \({\rm Q}\) の部分集合 )であるから、
\(x^2+y^2 {\small ~≦~} 1\) ならば \(x+y {\small ~≦~} \sqrt{\,2\,}\) である [終]
問題アーカイブ03
問題アーカイブ03\(x~,~y\) は実数とする。次の命題が成り立つことを証明せよ。
\({\small (1)}~\) \(x^2+y^2 {\small ~≦~} 8\) ならば \(x+y {\small ~≦~} 4\)
\({\small (2)}~\) \(x^2+y^2-6x-8y \lt 0\) ならば \(x \gt 0\) または \(y \gt 0\)
\({\small (1)}~\) \(x^2+y^2 {\small ~≦~} 8\) ならば \(x+y {\small ~≦~} 4\)
\({\small (2)}~\) \(x^2+y^2-6x-8y \lt 0\) ならば \(x \gt 0\) または \(y \gt 0\)
東京書籍|Advanced数学Ⅱ[701] p.105 問13
\({\small (1)}~\) [証明] 不等式 \(x^2+y^2 {\small ~≦~} 8\) は、
中心 \((0~,~0)\)、半径 \(2\sqrt{\,2\,}\) の円の内部および周上で、この領域を \({\rm P}\) とする
不等式 \(x+y {\small ~≦~} 4\) は、
\(\begin{eqnarray}~~~x+y&{\small ~≦~}&4
\\[3pt]~~~y&{\small ~≦~}&-x+4\end{eqnarray}\)
直線 \(y=-x+4\) の下側および直線上の領域で、この領域を \({\rm Q}\) とする
また、直線 \(x+y-4=0\) と原点 \((0~,~0)\) との距離 \(d\) は、
\(\begin{eqnarray}~~~d&=&\displaystyle \frac{\,|\,0+0-4\,|\,}{\,\sqrt{\,1^2+1^2\,}\,}
\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,\sqrt{\,2\,}\,}=\displaystyle \frac{\,4\sqrt{\,2\,}\,}{\,2\,}=2\sqrt{\,2\,}\end{eqnarray}\)
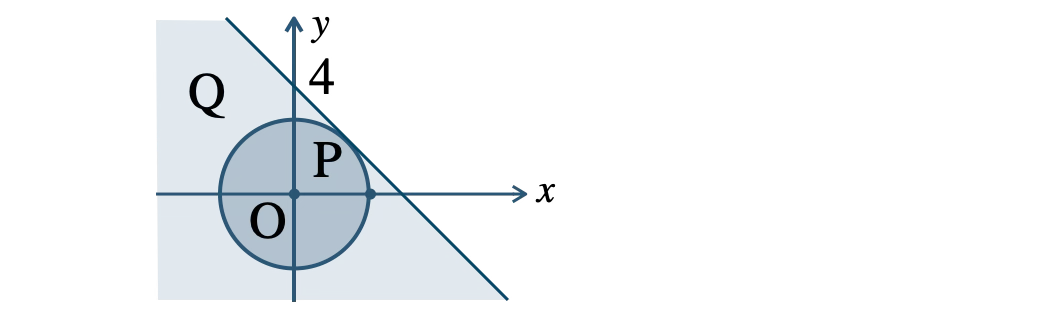

図より、\({\rm P} \subset {\rm Q}\)( \({\rm P}\) が \({\rm Q}\) の部分集合 )であるから、
\(x^2+y^2 {\small ~≦~} 8\) ならば \(x+y {\small ~≦~} 4\) である [終]
\({\small (2)}~\) [証明] 不等式 \(x^2+y^2-6x-8y \lt 0\) は、\(x\)、\(y\) について、平方完成すると、
\(\begin{eqnarray}~~~(x^2-6x)+(y^2-8y)&\lt&0
\\[3pt]~~~(x^2-6x+9)-9+(y^2-8y+16)-16&\lt&0
\\[3pt]~~~(x-3)^2+(y-4)^2&\lt&25\end{eqnarray}\)
\\[3pt]~~~(x^2-6x+9)-9+(y^2-8y+16)-16&\lt&0
\\[3pt]~~~(x-3)^2+(y-4)^2&\lt&25\end{eqnarray}\)
よって、中心 \((3~,~4)\)、半径 \(5\) の円の内部で、この領域を \({\rm P}\) とする
不等式 \(x \gt 0\) または \(y \gt 0\) の表す領域を \({\rm Q}\) とする
また、円 \({\rm P}\) の中心 \((3~,~4)\) と原点 \((0~,~0)\) との距離 \(d\) は、
\(\begin{eqnarray}~~~d&=&\sqrt{\,3^2+4^2\,}
\\[3pt]~~~&=&\sqrt{\,9+16\,}=\sqrt{\,25\,}=5\end{eqnarray}\)
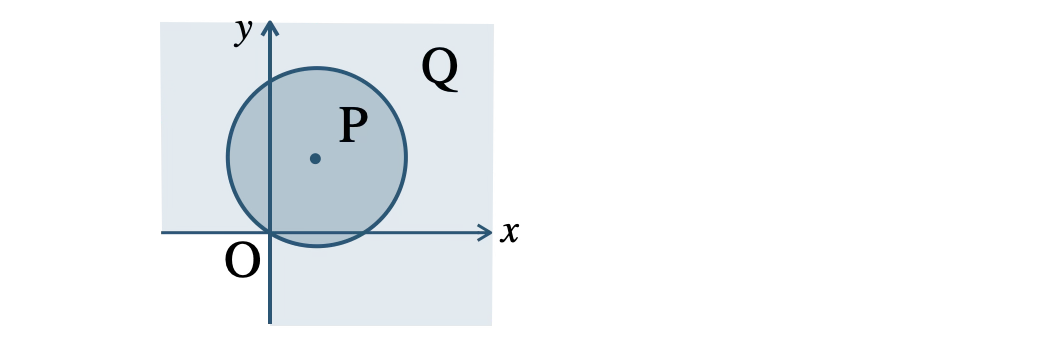

図より、\({\rm P} \subset {\rm Q}\)( \({\rm P}\) が \({\rm Q}\) の部分集合 )であるから、
\(x^2+y^2-6x-8y \lt 0\) ならば \(x \gt 0\) または \(y \gt 0\) である [終]
問題アーカイブ04
問題アーカイブ04次の命題が成り立つことを証明せよ。
\({\small (1)}~\) \(x^2+y^2-6x+8y+16 \lt 0\) ならば \(x \gt 0\) かつ \(y \lt 0\)
\({\small (2)}~\) \(x^2+y^2+2x-4y {\small ~≧~} 15\) ならば \(x^2+y^2 {\small ~≧~} 5\)
\({\small (1)}~\) \(x^2+y^2-6x+8y+16 \lt 0\) ならば \(x \gt 0\) かつ \(y \lt 0\)
\({\small (2)}~\) \(x^2+y^2+2x-4y {\small ~≧~} 15\) ならば \(x^2+y^2 {\small ~≧~} 5\)
東京書籍|Advanced数学Ⅱ[701] p.107 問21
\({\small (1)}~\) [証明] 不等式 \(x^2+y^2-6x+8y+16 \lt 0\) は、\(x\)、\(y\) について、平方完成すると、
\(\begin{eqnarray}~~~(x^2-6x)+(y^2+8y)+16&\lt&0
\\[3pt]~~~(x^2-6x+9)-9+(y^2+8y+16)-16+16&\lt&0
\\[3pt]~~~(x-3)^2+(y+4)^2&\lt&9\end{eqnarray}\)
\\[3pt]~~~(x^2-6x+9)-9+(y^2+8y+16)-16+16&\lt&0
\\[3pt]~~~(x-3)^2+(y+4)^2&\lt&9\end{eqnarray}\)
よって、中心 \((3~,~-4)\)、半径 \(3\) の円の内部で、この領域を \({\rm P}\) とする
不等式 \(x \gt 0\) かつ \(y \lt 0\) の表す領域(第4象限)を \({\rm Q}\) とする
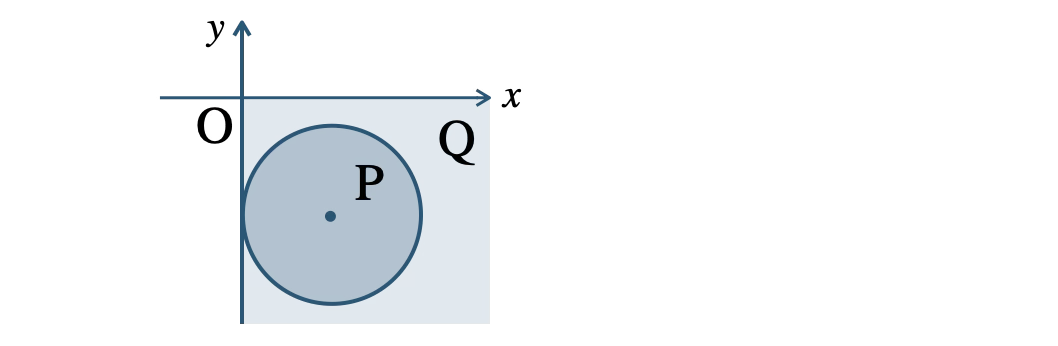

図より、\({\rm P} \subset {\rm Q}\)( \({\rm P}\) が \({\rm Q}\) の部分集合 )であるから、
\(x^2+y^2-6x+8y+16 \lt 0\) ならば \(x \gt 0\) かつ \(y \lt 0\) である [終]
\({\small (2)}~\) [証明] 不等式 \(x^2+y^2+2x-4y {\small ~≧~} 15\) は、\(x\)、\(y\) について、平方完成すると、
\(\begin{eqnarray}~~~(x^2+2x)+(y^2-4y)&{\small ~≧~}&15
\\[3pt]~~~(x^2+2x+1)-1+(y^2-4y+4)-4&{\small ~≧~}&15
\\[3pt]~~~(x+1)^2+(y-2)^2&{\small ~≧~}&20\end{eqnarray}\)
\\[3pt]~~~(x^2+2x+1)-1+(y^2-4y+4)-4&{\small ~≧~}&15
\\[3pt]~~~(x+1)^2+(y-2)^2&{\small ~≧~}&20\end{eqnarray}\)
よって、中心 \((-1~,~2)\)、半径 \(2\sqrt{\,5\,}\) の円の外部および周上で、この領域を \({\rm P}\) とする
不等式 \(x^2+y^2 {\small ~≧~} 5\) は、
中心 \((0~,~0)\)、半径 \(\sqrt{\,5\,}\) の円の外部および周上で、この領域を \({\rm Q}\) とする
また、2つの円の中心間の距離 \(d\) は、
\(\begin{eqnarray}~~~d&=&\sqrt{\,(-1)^2+2^2\,}
\\[3pt]~~~&=&\sqrt{\,1+4\,}=\sqrt{\,5\,}\end{eqnarray}\)
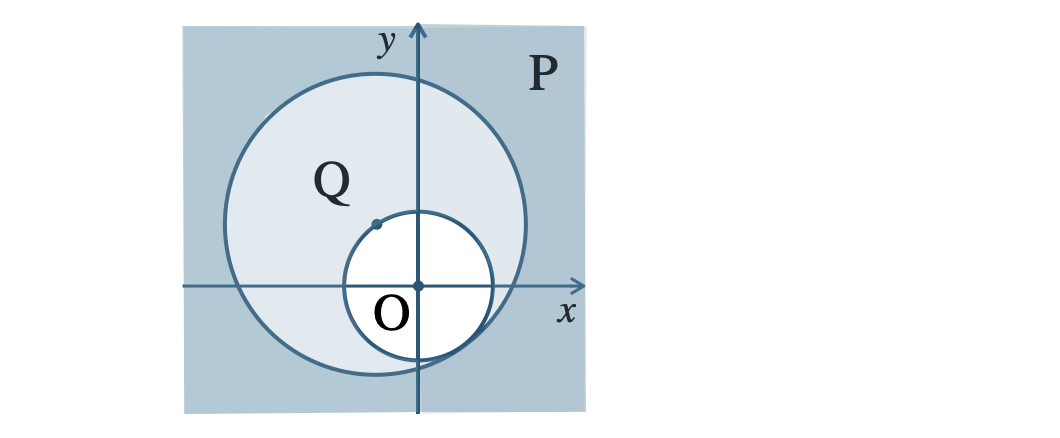

図より、\({\rm P} \subset {\rm Q}\)( \({\rm P}\) が \({\rm Q}\) の部分集合 )であるから、
\(x^2+y^2+2x-4y {\small ~≧~} 15\) ならば \(x^2+y^2 {\small ~≧~} 5\) である [終]
問題アーカイブ05
問題アーカイブ05次の命題が成り立つことを証明せよ。
\(x^2+y^2 \lt 2\) ならば \(x+y \lt 2\)
\(x^2+y^2 \lt 2\) ならば \(x+y \lt 2\)
東京書籍|Standard数学Ⅱ[702] p.112 Challenge 問1
[証明] 不等式 \(x^2+y^2 \lt 2\) は、
中心 \((0~,~0)\)、半径 \(\sqrt{\,2\,}\) の円の内部で、この領域を \({\rm P}\) とする
不等式 \(x+y \lt 2\) は、
\(\begin{eqnarray}~~~x+y&\lt&2
\\[3pt]~~~y&\lt&-x+2\end{eqnarray}\)
直線 \(y=-x+2\) の下側の領域で、この領域を \({\rm Q}\) とする
また、直線 \(x+y-2=0\) と原点 \((0~,~0)\) との距離 \(d\) は、
\(\begin{eqnarray}~~~d&=&\displaystyle \frac{\,|\,0+0-2\,|\,}{\,\sqrt{\,1^2+1^2\,}\,}
\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,\sqrt{\,2\,}\,}=\sqrt{\,2\,}\end{eqnarray}\)
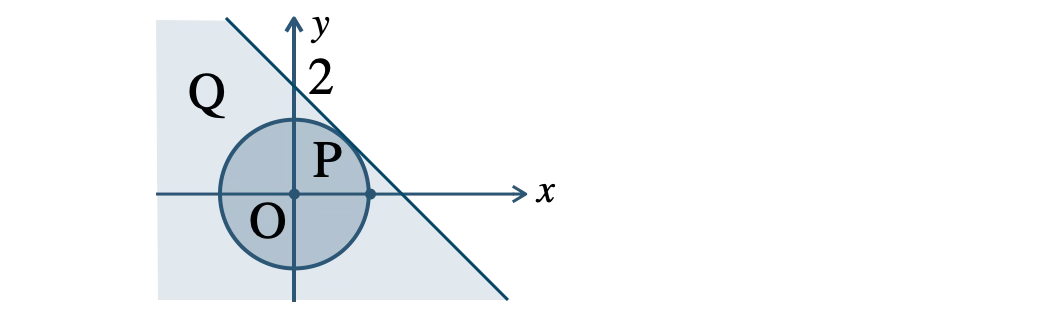

図より、\({\rm P} \subset {\rm Q}\)( \({\rm P}\) が \({\rm Q}\) の部分集合 )であるから、
\(x^2+y^2 \lt 2\) ならば \(x+y \lt 2\) である [終]


