- 数学Ⅱ|図形と方程式「領域と円の最大値・最小値」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|領域と円の最大値・最小値
図形と方程式 70☆\(x~,~y\) が不等式 \(x-y+1{\small ~≧~}0~,~\)\(x-3y+3{\small ~≦~}0~,~\)\(3x-y-7{\small ~≦~}0\) を満たすとき、\(x^2+y^2\) の最大値・最小値の求め方は?
高校数学Ⅱ|図形と方程式
解法のPoint
領域と円の最大値・最小値
Point:領域と円の最大値・最小値
① 不等式の領域を図示し、三角形の頂点の座標を求める。
② \(x^2+y^2=k\) とおき、中心 \((0~,~0)\) で半径 \(\sqrt{\,k\,}\) の円の方程式とする。
③ 円が領域内で共有点をもつとき、半径が最大のとき最大値、半径が最小のとき最小値となる。


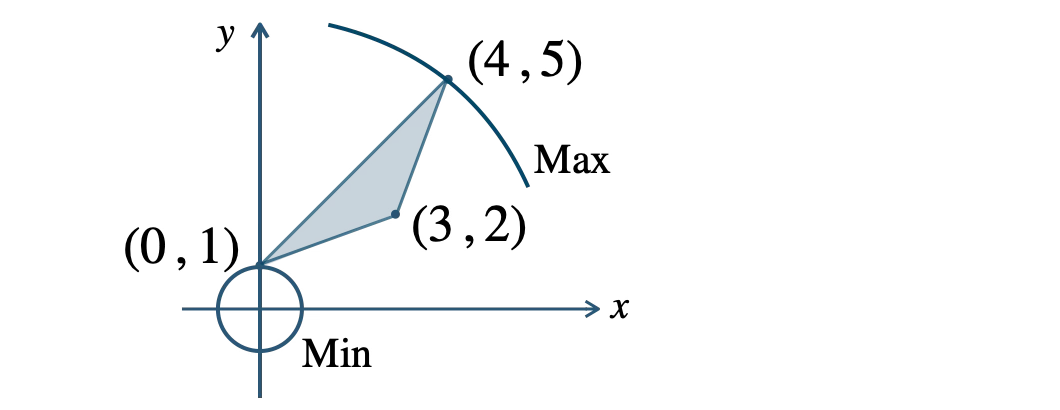
3直線がつくる領域と円の最大値・最小値は、
① 不等式の領域を図示し、三角形の頂点の座標を求める。
② \(x^2+y^2=k\) とおき、中心 \((0~,~0)\) で半径 \(\sqrt{\,k\,}\) の円の方程式とする。
③ 円が領域内で共有点をもつとき、半径が最大のとき最大値、半径が最小のとき最小値となる。



©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|領域と円の最大値・最小値
図形と方程式 70☆
\(x~,~y\) が不等式 \(x-y+1{\small ~≧~}0~,~\)\(x-3y+3{\small ~≦~}0~,~\)\(3x-y-7{\small ~≦~}0\) を満たすとき、\(x^2+y^2\) の最大値・最小値の求め方は?
高校数学Ⅱ|図形と方程式
不等式 \(x-y+1{\small ~≧~}0\) は、
\(\begin{eqnarray}~~~x-y+1&{\small ~≧~}&0
\\[3pt]~~~-y&{\small ~≧~}&-x-1
\\[3pt]~~~y&{\small ~≦~}&x+1\end{eqnarray}\)
よって、直線 \(y=x+1\) の下側
不等式 \(x-3y+3{\small ~≦~}0\) は、
\(\begin{eqnarray}~~~x-3y+3&{\small ~≦~}&0
\\[3pt]~~~-3y&{\small ~≦~}&-x-3
\\[3pt]~~~y&{\small ~≧~}&\displaystyle \frac{\,1\,}{\,3\,}x+1\end{eqnarray}\)
よって、直線 \(y=\displaystyle \frac{\,1\,}{\,3\,}x+1\) の上側
不等式 \(3x-y-7{\small ~≦~}0\) は、
\(\begin{eqnarray}~~~-y&{\small ~≦~}&-3x+7
\\[3pt]~~~y&{\small ~≧~}&3x-7\end{eqnarray}\)
よって、直線 \(y=3x-7\) の上側
次に、2直線 \(x-y+1=0\)、\(x-3y+3=0\) の交点は、
\(\begin{eqnarray}~~~~~x-y+1&=&0
\\~-\big{)}~~~x-3y+3&=&0
\\\hline 2y-2&=&0
\\[3pt] 2y&=&2
\\[3pt] y&=&1\end{eqnarray}\)
\(x-y+1=0\) に代入して、
\(\begin{eqnarray}~~~x-1+1&=&0
\\[3pt]~~~x&=&0\end{eqnarray}\)
よって、\((0~,~1)\)
また、2直線 \(x-3y+3=0\)、\(3x-y-7=0\) の交点は、
\(\begin{eqnarray}~~~~~
x-3y+3&=&0 \\~-\big{)}~~~9x-3y-21&=&0
\\\hline -8x+24&=&0
\\[3pt] -8x&=&-24
\\[3pt] x&=&3\end{eqnarray}\)
\(3x-y-7=0\) に代入して、
\(\begin{eqnarray}~~~9-y-7&=&0
\\[3pt]~~~-y&=&-2
\\[3pt]~~~y&=&2\end{eqnarray}\)
よって、\((3~,~2)\)
さらに、2直線 \(x-y+1=0\)、\(3x-y-7=0\) の交点は、
\(\begin{eqnarray}~~~~~
x-y+1&=&0
\\~-\big{)}~~~3x-y-7&=&0
\\\hline -2x+8&=&0
\\[3pt] -2x&=&-8
\\[3pt] x&=&4\end{eqnarray}\)
\(x-y+1=0\) に代入して、
\(\begin{eqnarray}~~~4-y+1&=&0
\\[3pt]~~~-y&=&-5
\\[3pt]~~~y&=&5\end{eqnarray}\)
よって、\((4~,~5)\)
以上より、この連立不等式の表す領域は、3点 \((0~,~1)\)、\((3~,~2)\)、\((4~,~5)\) を頂点とする三角形の周および内部である


ここで、\(x^2+y^2=k\) とおくと、
\(x^2{\small ~≧~}0\)、\(y^2{\small ~≧~}0\) より \(k{\small ~≧~}0\) で、中心 \((0~,~0)\)、半径 \(\sqrt{\,k\,}\) の円となる
この円が領域内で共有点をもつとき、半径が最大で \(x^2+y^2\) が最大値、半径が最小で \(x^2+y^2\) が最小値となる



点 \((4~,~5)\) をとるとき半径が最大で、
最大値 \(4^2+5^2=16+25=41\)
点 \((0~,~1)\) をとるとき半径が最小で、
最小値 \(0^2+1^2=1\)
したがって、
\(x=4~,~y=5\) のとき、最大値 \(41\)
\(x=0~,~y=1\) のとき、最小値 \(1\) となる



