- 数学Ⅱ|図形と方程式「線形計画法の文章問題」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|線形計画法の文章問題
図形と方程式 71☆Xは \(1~{\rm g}\) あたり成分aを \(3~{\rm mg}\)、成分bを \(1~{\rm mg}\) 含み、Yは \(1~{\rm g}\) あたり成分aを \(1~{\rm mg}\)、成分bを \(2~{\rm mg}\) 含むとき、aを \(9~{\rm mg}\) 以上でbを \(8~{\rm mg}\) 以上取り、XとYの合計を最小にするときのXとYはそれぞれ何 \({\rm g}\) 取ればよいか?
高校数学Ⅱ|図形と方程式
解法のPoint
線形計画法の文章問題
Point:線形計画法の文章問題
① 文章より、条件についての連立不等式をつくり、領域を求める。
② 最大値(最小値)を求めたいものを \(k\) とおき、図形の方程式とする。
③ この図形が領域内で共有点をもつときの \(k\) の最大値(最小値)を求める。
線形計画法の文章問題は、
① 文章より、条件についての連立不等式をつくり、領域を求める。
② 最大値(最小値)を求めたいものを \(k\) とおき、図形の方程式とする。
③ この図形が領域内で共有点をもつときの \(k\) の最大値(最小値)を求める。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|線形計画法の文章問題
図形と方程式 71☆
Xは \(1~{\rm g}\) あたり成分aを \(3~{\rm mg}\)、成分bを \(1~{\rm mg}\) 含み、Yは \(1~{\rm g}\) あたり成分aを \(1~{\rm mg}\)、成分bを \(2~{\rm mg}\) 含むとき、aを \(9~{\rm mg}\) 以上でbを \(8~{\rm mg}\) 以上取り、XとYの合計を最小にするときのXとYはそれぞれ何 \({\rm g}\) 取ればよいか?
高校数学Ⅱ|図形と方程式
\(~~~\begin{array}{c|cc}
& a & b \\
\hline
X & 3{\rm mg} & 1{\rm mg} \\
Y & 1{\rm mg} & 2{\rm mg}
\end{array}\)
Xを \(x~{\rm g}\)、Yを \(y~{\rm g}\) 取るとき、
\(x{\small ~≧~}0~,~y{\small ~≧~}0~~~\cdots {\small [\,1\,]}\)
成分 a は \(9~{\rm mg}\) 以上なので、
\(3x+y{\small ~≧~}9~~~\cdots {\small [\,2\,]}\)
成分 b は \(8~{\rm mg}\) 以上なので、
\(x+2y{\small ~≧~}8~~~\cdots {\small [\,3\,]}\)
\({\small [\,2\,]}\) より、
\(\begin{eqnarray}~~~3x+y&{\small ~≧~}&9\\[3pt]~~~y&{\small ~≧~}&-3x+9\end{eqnarray}\)
これより、直線 \(y=-3x+9\) の上側
\({\small [\,3\,]}\) より、
\(\begin{eqnarray}~~~x+2y&{\small ~≧~}&8\\[3pt]~~~2y&{\small ~≧~}&-x+8\\[3pt]~~~y&{\small ~≧~}&-\displaystyle \frac{\,1\,}{\,2\,}x+4\end{eqnarray}\)
これより、直線 \(y=-\displaystyle \frac{\,1\,}{\,2\,}x+4\) の上側
また、\(3x+y=9\) 、\(x+2y=8\) の交点は、
\(\begin{eqnarray}~~~~~
6x+2y&=&18 \\~-\big{)}~~~x+2y&=&8\\
\hline 5x&=&10
\\[3pt] x&=&2\end{eqnarray}\)
\(3x+y=9\) に代入して、
\(\begin{eqnarray}~~~6+y&=&9\\[3pt]~~~y&=&3\end{eqnarray}\)
よって、\((2~,~3)\)
以上より、\({\small [\,1\,]}\) 〜 \({\small [\,3\,]}\) の連立不等式の領域は、
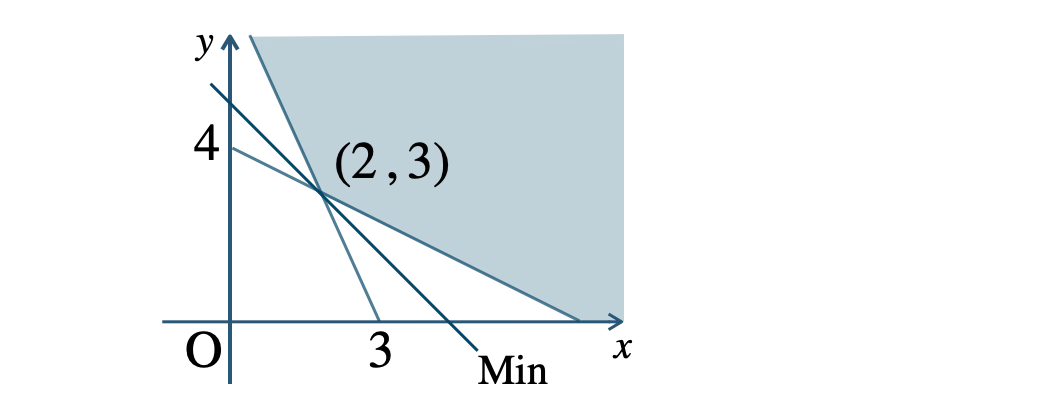

ただし、境界線を含む
ここで、XとYの合計を \(k\) とすると、
\(\begin{eqnarray}~~~x+y&=&k\\[3pt]~~~y&=&-x+k\end{eqnarray}\)
傾き \(-1\) 、\(y\) 切片は \(k\) の直線であり、領域内で動くとき、
\(y\) 切片が最小で、\(x+y\) が最小値をとるので、
点 \((2~,~3)\) となるときで、
最小値 \(2+3=5\)
したがって、Xを \(2~{\rm g}\)、Yを \(3~{\rm g}\) とればよい



