等差数列の和の最大値・最小値

初項 \( a=30 \)、公差 \( d=-4 \) の等差数列の一般項は、

---

\(\begin{eqnarray}~~~a_n&=&30+(n-1)\cdot(-4)
\\[3pt]~~~&=&30-4n+4
\\[3pt]~~~&=&34-4n
\end{eqnarray}\)

 

ここで、\( a_n\lt 0 \) となる \( n \) の範囲は、

---

\(\begin{eqnarray}~~~a_n=34-4n&\lt &0
\\[3pt]~~~-4n&\lt &-34
\\[3pt]~~~n&\gt &\displaystyle \frac{\,34\,}{\,4\,}=8.5
\end{eqnarray}\)

---

\( n \) は自然数より、\( n=9 \) 以上で負の項となる

---

よって、初めて負となるのは第 \(9\) 項である

 

次に、\( a_1\sim a_8 \) までは正の項で、部分和 \(S_n\) は増加するが、
\(a_n\lt 0\) となる \(n=9\) 以降は減少する

---

---

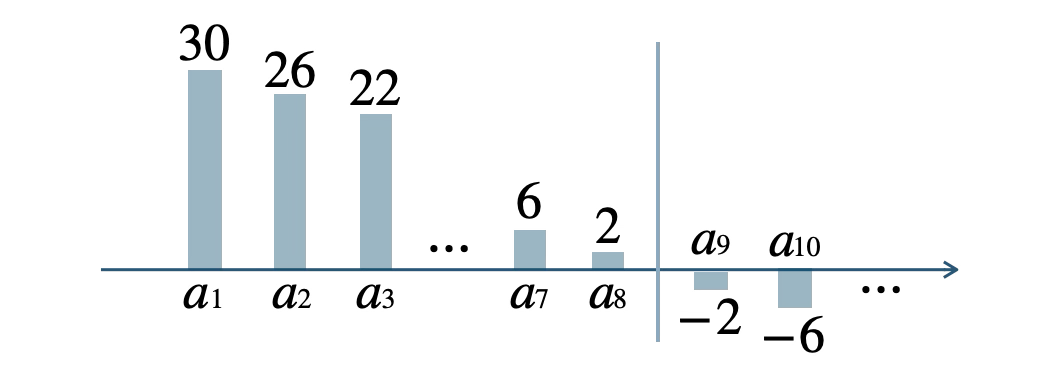
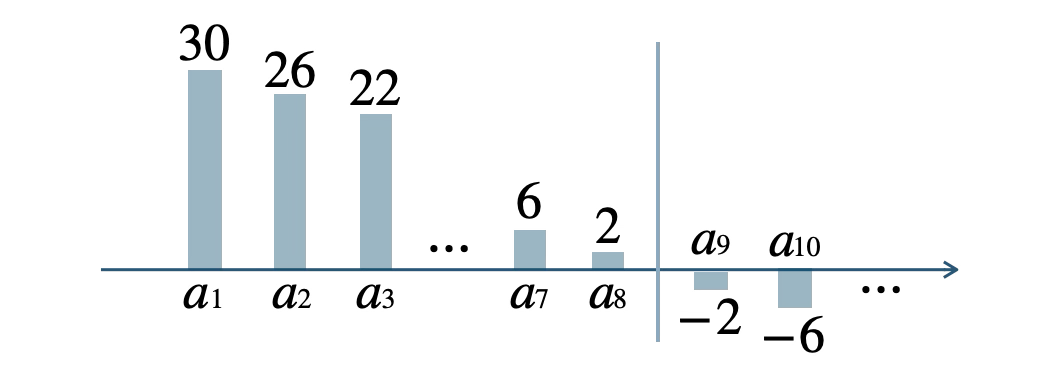
よって、\( a_1\sim a_8 \) の和が最大値であるので、

---

初項 \( a=30 \)、公差 \( d=-4 \)、項数 \( n=8 \) の等差数列の和の公式より、

---

\(\begin{eqnarray}~~~S_8&=&\displaystyle \frac{\,1\,}{\,2\,}\cdot 8 \cdot \left\{\,2\cdot 30 + (8-1)\cdot(-4)\,\right\}
\\[5pt]~~~&=&4\cdot\left\{\,60+7\cdot(-4)\,\right\}
\\[3pt]~~~&=&4\cdot(60-28)
\\[3pt]~~~&=&4\cdot 32
\\[3pt]~~~&=&128
\end{eqnarray}\)