- 数学B｜数列「図形の性質と漸化式」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題｜図形の性質と漸化式
高校数学B｜数列
解法のPoint
図形の性質と漸化式
図形の性質を表した漸化式の解法は、
① \( n=1 \) とき \( a_1 \) の値を求める。
直線が1本のとき、\( a_1=0 \)
② \( n=2~,~3~,~4~,~\cdots \) と増やしたときを調べて、\( a_n \) と \( a_{n+1} \) の関係を求める。
直線が2本のとき、交点は \( a_2=1 \)
直線が3本のとき、交点が2個増えて、
\(a_3=1+2=3\)
直線が4本のとき、交点が3個増えて、
\(a_4=3+3=6\)
③ \( n+1 \) 項目と \( n \) 項目の関係から、\( a_{n+1} \) と \( a_n \) の漸化式を立てる。
\( n+1 \) 本目を引くとき、
もとの \( n \) 本の直線と \(n\) 個の交点ができ、
もとの \( a_n \) 個と加えて、
\(a_{n+1}=a_n+n\)
④ 漸化式より、階差数列を用いて、一般項 \( a_n \) を求める。
©︎ 2025 教科書より詳しい高校数学 yorikuwa.com
詳しい解説｜図形の性質と漸化式
どの2本も平行でなく、どの3本も1点で交わらない \(n\) 本の直線によってつくられる交点の個数 \(a_n\) の求め方は？
高校数学B｜数列
\( n=1 \) のとき、
1本の直線には交点がないので、\( a_1=0 \) 個
\( n=2 \) のとき、
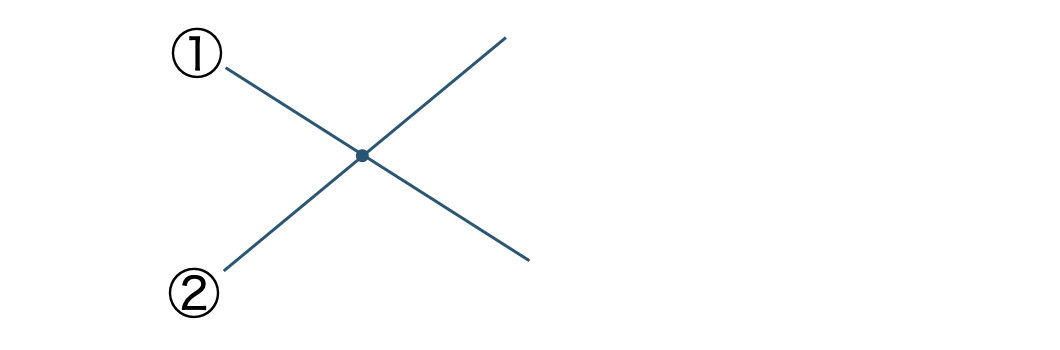
2本目の直線を引くとき、もとの1本と交点が1個できるので、\( a_2=1 \) 個
\( n=3 \) のとき、
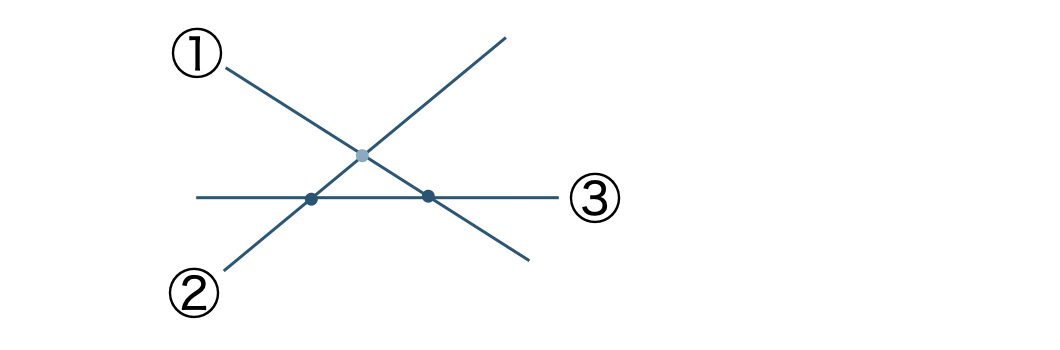
3本目の直線を引くとき、もとの2本と交点が2個できるので、\( a_3=1+2=3 \) 個
\( n=4 \) のとき、
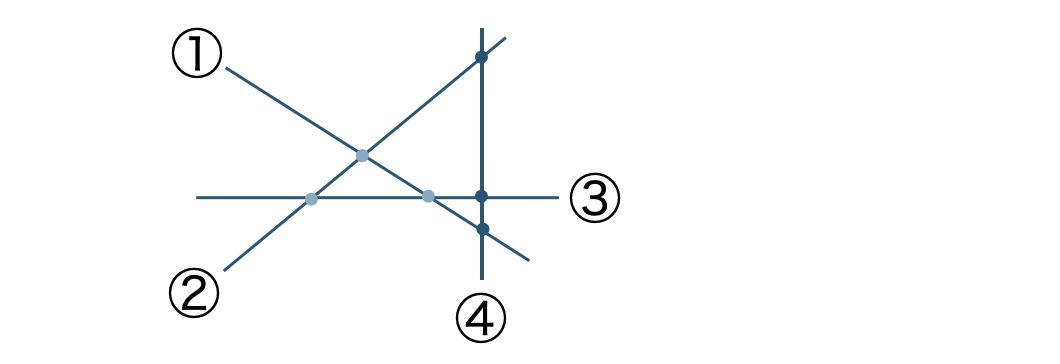
4本目を追加するとき、もとの3本と交点が3個できるので、\( a_4=3+3=6 \) 個
これより、\( n+1 \) 本目を引いたとき、もとの \( n \) 本と交点が \( n \) 個でき、もとから \( a_n \) 個あるので、
\(\begin{eqnarray}~~~a_{n+1}&=&a_n+n\end{eqnarray}\)
が成り立つ
よって、\(a_{n+1}-a_n=n\) より、
この数列 \( \{a_n\} \) の階差数列 \( \{b_n\} \) は一般項 \( b_n=n \)
\( n{\small ~≧~}2 \) のとき、
\(\begin{eqnarray}~~~a_n&=&a_1+\displaystyle \sum_{k=1}^{\,n-1} b_k
\\[5pt]~~~&=&0+\displaystyle \sum_{k=1}^{\,n-1} k \hspace{20pt}(\,∵~ a_1=0~,~b_k=k\,)
\end{eqnarray}\)
\(\displaystyle\sum_{k=1}^{n} k=\displaystyle\frac{\,1\,}{\,2\,}n(n+1)\) の \(n\to n-1\) と置き換えると、
\(\begin{eqnarray}~~~~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(n-1)\left\{(n-1)+1\right\}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(n-1)\,n~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
\(n=1\) のとき、\({\small [\,1\,]}\) より、
\(\begin{eqnarray}~~~a_1&=&\displaystyle \frac{\,1\,}{\,2\,}\cdot(1-1)\cdot1=0
\end{eqnarray} \)
これより、\(n=1\) のときも \({\small [\,1\,]}\) が成り立つ
したがって、\(a_n=\displaystyle \frac{\,1\,}{\,2\,}(n-1)\,n\)
どの2本も平行でなく、どの3本も1点で交わらない \(n\) 本の直線によってつくられる平面の個数 \(a_n\) の求め方は？
高校数学B｜数列
\(n=1\) のとき、
1本の直線で、平面は2個できるので \( a_1=2 \)
\(n=2\) のとき、
2本目の直線で、もとの直線と1点で交わり、
この直線は、この点で2つの部分に分けられて、平面は2個増加する
よって、\( a_2=2+2=4 \)
\(n=3\) のとき、
3本目の直線で、もとの直線と2点で交わり、
この直線は、この2点で3つの部分に分けられて、平面は3個増加する
よって、\( a_3=4+3=7 \)
\(n=4\) のとき、
4本目の直線で、もとの直線と3点で交わり、
この直線は、この3点で4つの部分に分けられて、平面は4個増加する
よって、\( a_4=7+4=11 \)
これより、\( n+1 \) 本目の直線を引いたとき、もとの直線と \( n \) 点で交わり、
この直線は、これらの \( n \) 点で \( n+1 \) 個の部分に分けられて、平面が \( n+1 \) 個増加する
よって、もとから \( a_n \) 個あるので、
\(\begin{eqnarray}~~~a_{n+1}&=&a_n+(n+1)\end{eqnarray}\)
\(a_{n+1}-a_n=n+1\) より、
この数列 \( \{a_n\} \) の階差数列 \( \{b_n\} \) の一般項は \( b_n=n+1 \)
\( n{\small ~≧~}2 \) のとき、
\(\begin{eqnarray}~~~a_n&=&a_1+\displaystyle \sum_{k=1}^{\,n-1} b_k
\\[5pt]~~~&=&2+\displaystyle \sum_{k=1}^{\,n-1}(k+1)
\\[5pt]~~~&=&2+\displaystyle \sum_{k=1}^{\,n-1}k+\displaystyle \sum_{k=1}^{\,n-1}1
\end{eqnarray}\)
\(\displaystyle\sum_{k=1}^{n} k=\displaystyle\frac{\,1\,}{\,2\,}n(n+1)\) の \(n\to n-1\) と置き換えると、
\(\begin{eqnarray}~~~~~~&=&2+\displaystyle \frac{\,1\,}{\,2\,}(n-1)\left\{(n-1)+1\right\}+(n-1)
\\[5pt]~~~&=&2+\displaystyle \frac{\,1\,}{\,2\,}(n-1)\,n+(n-1)
\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,2\,}+\displaystyle \frac{\,1\,}{\,2\,}(n-1)\,n+\displaystyle \frac{\,2\,}{\,2\,}(n-1)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\left\{4+(n-1)\,n+2(n-1)\right\}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(4+n^2-n+2n-2)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(n^2+n+2)~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
\(n=1\) のとき、\({\small [\,1\,]}\) より、
\(\begin{eqnarray}~~~a_1&=&\displaystyle \frac{\,1\,}{\,2\,}\cdot(1^2+1+2)=\displaystyle \frac{\,1\,}{\,2\,}\cdot 4=2
\end{eqnarray} \)
これより、\(n=1\) のときも \({\small [\,1\,]}\) が成り立つ
したがって、\(a_n=\displaystyle \frac{\,1\,}{\,2\,}(n^2+n+2)\)
