このページは、「図形の性質と漸化式」の練習問題アーカイブページとなります。
この問題の解き方の詳細は↓
図形の性質と漸化式 で確認できます。
問題アーカイブ01
数研出版|数学B[710] p.37 応用例題6
数研出版|高等学校数学B[711] p.39 研究 例1
東京書籍|Advanced数学B[701] p.35 応用例題3
\(n=1\) のとき、

1本の直線で、平面は2個できるので \( a_1=2 \)
\(n=2\) のとき、
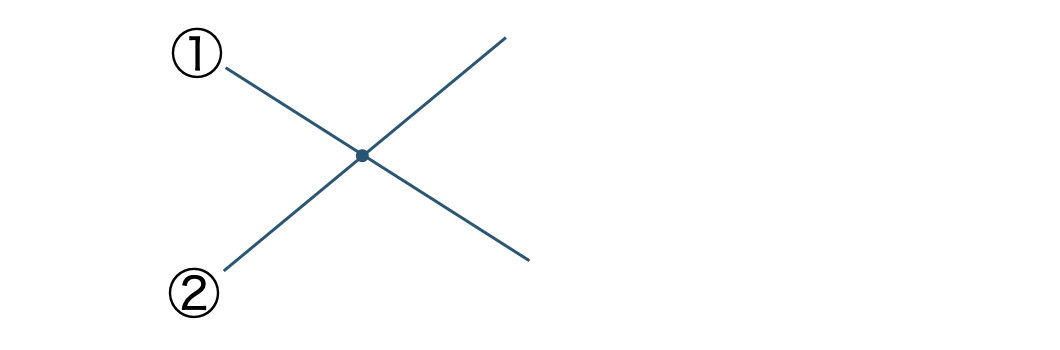
2本目の直線で、もとの直線と1点で交わり、
この直線は、この点で2つの部分に分けられて、平面は2個増加する
よって、\( a_2=2+2=4 \)
\(n=3\) のとき、
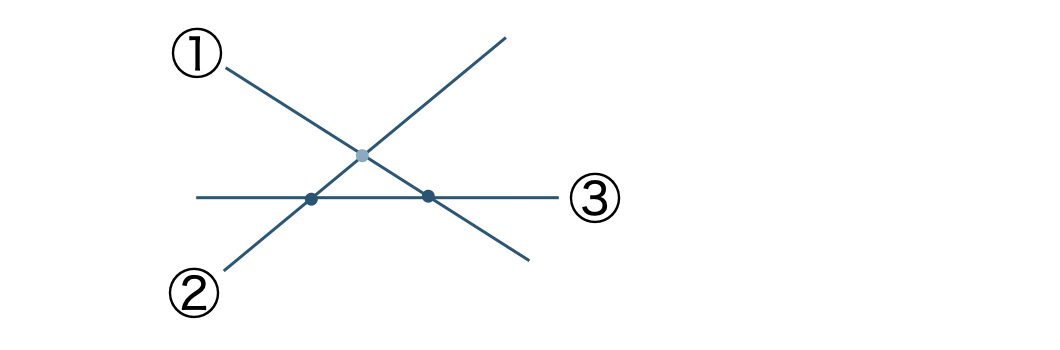
3本目の直線で、もとの直線と2点で交わり、
この直線は、この2点で3つの部分に分けられて、平面は3個増加する
よって、\( a_3=4+3=7 \)
\(n=4\) のとき、
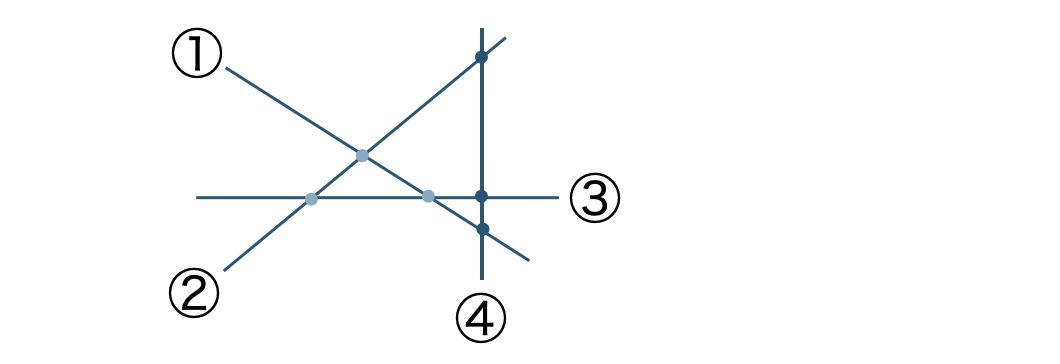
4本目の直線で、もとの直線と3点で交わり、
この直線は、この3点で4つの部分に分けられて、平面は4個増加する
よって、\( a_4=7+4=11 \)
これより、\( n+1 \) 本目の直線を引いたとき、もとの直線と \( n \) 点で交わり、
この直線は、これらの \( n \) 点で \( n+1 \) 個の部分に分けられて、平面が \( n+1 \) 個増加する
よって、もとから \( a_n \) 個あるので、
\(\begin{eqnarray}~~~a_{n+1}&=&a_n+(n+1)\end{eqnarray}\)
\(a_{n+1}-a_n=n+1\) より、
この数列 \( \{a_n\} \) の階差数列 \( \{b_n\} \) の一般項は \( b_n=n+1 \)
\( n{\small ~≧~}2 \) のとき、
\(\begin{eqnarray}~~~a_n&=&a_1+\displaystyle \sum_{k=1}^{\,n-1} b_k
\\[5pt]~~~&=&2+\displaystyle \sum_{k=1}^{\,n-1}(k+1)
\\[5pt]~~~&=&2+\displaystyle \sum_{k=1}^{\,n-1}k+\displaystyle \sum_{k=1}^{\,n-1}1
\end{eqnarray}\)
\(\displaystyle\sum_{k=1}^{n} k=\displaystyle\frac{\,1\,}{\,2\,}n(n+1)\) の \(n\to n-1\) と置き換えると、
\(\begin{eqnarray}~~~~~~&=&2+\displaystyle \frac{\,1\,}{\,2\,}(n-1)\left\{(n-1)+1\right\}+(n-1)
\\[5pt]~~~&=&2+\displaystyle \frac{\,1\,}{\,2\,}(n-1)\,n+(n-1)
\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,2\,}+\displaystyle \frac{\,1\,}{\,2\,}(n-1)\,n+\displaystyle \frac{\,2\,}{\,2\,}(n-1)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\left\{4+(n-1)\,n+2(n-1)\right\}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(4+n^2-n+2n-2)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(n^2+n+2)~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
\(n=1\) のとき、\({\small [\,1\,]}\) より、
\(\begin{eqnarray}~~~a_1&=&\displaystyle \frac{\,1\,}{\,2\,}\cdot(1^2+1+2)=\displaystyle \frac{\,1\,}{\,2\,}\cdot 4=2
\end{eqnarray} \)
これより、\(n=1\) のときも \({\small [\,1\,]}\) が成り立つ
したがって、\(a_n=\displaystyle \frac{\,1\,}{\,2\,}(n^2+n+2)\)
問題アーカイブ02
\({\small (1)}~\) \( a_4 \) を求めよ。
\({\small (2)}~\) \( a_{n+1} \) を \( a_n \) の式で表せ。
\({\small (3)}~\) \( a_n \) を求めよ。
東京書籍|Advanced数学B[701] p.41 問題 12
\({\small (1)}~\)
四角形の対角線の本数は2本なので、\( a_4=2 \)
\({\small (2)}~\)
\( n \) 角形に1つの頂点を追加して \( n+1 \) 角形にしたとき、
新しい頂点から、隣り合う2点を除く \( n-2 \) 個の頂点へ対角線が引ける
ここで、隣り合う2点を結ぶ線分も対角線となり、新たに対角線は合計 \( n-1 \) 本増えることになる
よって、もとから \( a_n \) 本あるので、
\(\begin{eqnarray}~~~a_{n+1}&=&a_n+(n-1)\end{eqnarray}\)
\({\small (3)}~\)
\(a_{n+1}-a_n=n-1\) より、
この数列 \( \{a_n\} \) の階差数列 \( \{b_n\} \) の一般項は \( b_n=n-1 \)
\( n{\small ~≧~}5 \) のとき、
\(\begin{eqnarray}~a_n&=&a_4+\displaystyle \sum_{k=4}^{\,n-1} b_k
\\[5pt]~&=&2+\displaystyle \sum_{k=4}^{\,n-1}(k-1)
\\[5pt]~~~&=&2+\displaystyle \sum_{k=4}^{\,n-1}k-\displaystyle \sum_{k=4}^{\,n-1}1
\end{eqnarray}\)
\(\displaystyle\sum_{k=1}^{n} k=\displaystyle\frac{\,1\,}{\,2\,}n(n+1)\) を用いて計算すると、
\(\begin{eqnarray}~~&=&2+\left\{\displaystyle \frac{\,1\,}{\,2\,}(n-1)\,n-\displaystyle \frac{\,1\,}{\,2\,}\cdot 3\cdot 4\right\}-(n-4)
\\[5pt]~&=&2+\displaystyle \frac{\,1\,}{\,2\,}(n-1)\,n-6-n+4
\\[5pt]~&=&\displaystyle \frac{\,1\,}{\,2\,}(n-1)\,n-n
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\left\{(n-1)\,n-2n\right\}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(n^2-n-2n)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(n^2-3n)
\\[5pt]~~~&=&\displaystyle \frac{\,n(n-3)\,}{\,2\,}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
\(n=4\) のとき、\({\small [\,1\,]}\) より、
\(\begin{eqnarray}~~~a_4&=&\displaystyle \frac{\,4(4-3)\,}{\,2\,}=\displaystyle \frac{\,4\,}{\,2\,}=2
\end{eqnarray} \)
これより、\(n=4\) のときも \({\small [\,1\,]}\) が成り立つ
したがって、\(a_n=\displaystyle \frac{\,n(n-3)\,}{\,2\,}\)
問題アーカイブ03
東京書籍|Advanced数学B[701] p.45 練習問題B 15
\(n=1\) のとき、
1つの円で、平面は2個できるので \( a_1=2 \)
\(n=2\) のとき、
2つ目の円で、もとの円と2点で交わり、
この円は、この2点で2つの部分に分けられて、平面は2個増加する
よって、\( a_2=2+2=4 \)
\(n=3\) のとき、
3つ目の円で、もとの2つの円と4点で交わり、
この円は、この4点で4つの部分に分けられて、平面は4個増加する
よって、\( a_3=4+4=8 \)
\(n=4\) のとき、
4つ目の円で、もとの3つの円と6点で交わり、
この円は、この6点で6つの部分に分けられて、平面は6個増加する
よって、\( a_4=8+6=14 \)
これより、\( n+1 \) 個目の円を描いたとき、もとの \( n \) 個の円と \( 2n \) 点で交わり、
この円は、これらの \( 2n \) 点で \( 2n \) 個の部分に分けられて、平面が \( 2n \) 個増加する
よって、もとから \( a_n \) 個あるので、
\(\begin{eqnarray}~~~a_{n+1}&=&a_n+2n\end{eqnarray}\)
\(a_{n+1}-a_n=2n\) より、
この数列 \( \{a_n\} \) の階差数列 \( \{b_n\} \) の一般項は \( b_n=2n \)
\( n{\small ~≧~}2 \) のとき、
\(\begin{eqnarray}~a_n&=&a_1+\displaystyle \sum_{k=1}^{\,n-1} b_k
\\[5pt]~&=&2+\displaystyle \sum_{k=1}^{\,n-1}2k
\\[5pt]~~~&=&2+2\displaystyle \sum_{k=1}^{\,n-1}k
\end{eqnarray}\)
\(\displaystyle\sum_{k=1}^{n} k=\displaystyle\frac{\,1\,}{\,2\,}n(n+1)\) の \(n\to n-1\) と置き換えると、
\(\begin{eqnarray}~~&=&2+2\cdot\displaystyle \frac{\,1\,}{\,2\,}(n-1)\left\{(n-1)+1\right\}
\\[5pt]~&=&2+(n-1)\,n
\\[5pt]~&=&2+n^2-n
\\[5pt]~~~&=&n^2-n+2~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
\(n=1\) のとき、\({\small [\,1\,]}\) より、
\(\begin{eqnarray}~~~a_1&=&1^2-1+2=2
\end{eqnarray} \)
これより、\(n=1\) のときも \({\small [\,1\,]}\) が成り立つ
したがって、\(a_n=n^2-n+2\)


