- 数学B|統計的な推測「確率密度関数と確率」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|確率密度関数と確率
高校数学B|統計的な推測
解法のPoint
確率密度関数と確率
連続的な確率変数 \( X \) を「連続型確率変数」といい、\( f(x) \) を \( X \) の「確率密度関数」という。
確率密度関数の指定された範囲での確率の求め方は、
① 確率密度関数 \( y=f(x) \) のグラフをかく。
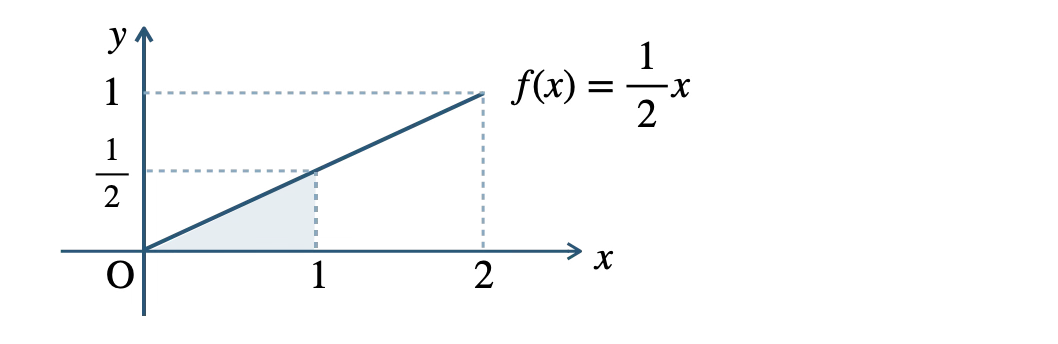
② 指定された範囲の \( y=f(x) \) と \( x \) 軸で囲まれた面積が確率の値となる。
\(\begin{eqnarray}~~~P(\,0{\small ~≦~}X{\small ~≦~}1\,)=\displaystyle \frac{\,1\,}{\,2\,}\cdot 1 \cdot \displaystyle \frac{\,1\,}{\,2\,}=\displaystyle \frac{\,1\,}{\,4\,}\end{eqnarray}\)
また、積分を用いると、
\(\begin{eqnarray}~~~\displaystyle \int_{0}^{1}\displaystyle \frac{\,1\,}{\,2\,}x\,dx=\left[\,\displaystyle \frac{\,1\,}{\,4\,}x^{2}\,\right]_{0}^{1}=\displaystyle \frac{\,1\,}{\,4\,}\end{eqnarray}\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|確率密度関数と確率
確率変数 \( X \) の確率密度関数が \( f(x)=\displaystyle \frac{\,1\,}{\,2\,}x \,\,(\,0{\small ~≦~}x{\small ~≦~}2\,) \) のとき、確率 \( P(\,0{\small ~≦~}X{\small ~≦~}1\,) \) 、 \( P(\,1{\small ~≦~}X{\small ~≦~}2\,) \) の求め方は?
高校数学B|統計的な推測
\( f(x)=\displaystyle \frac{\,1\,}{\,2\,}x \,\,(\,0{\small ~≦~}x{\small ~≦~}2\,) \) のグラフは、
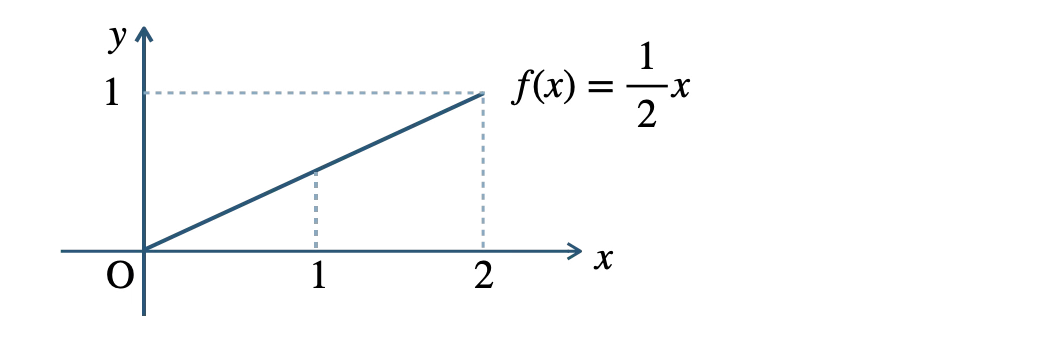
確率 \( P(\,0{\small ~≦~}X{\small ~≦~}1\,) \) は、以下の面積となるので、

\(\begin{eqnarray}~~~P(\,0{\small ~≦~}X{\small ~≦~}1\,)&=&\displaystyle \frac{\,1\,}{\,2\,}\cdot 1 \cdot \displaystyle \frac{\,1\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}
\end{eqnarray}\)
【別解】積分を用いると、
\(\begin{eqnarray}~~~\displaystyle \int_{0}^{1}\displaystyle \frac{\,1\,}{\,2\,}x\,dx&=&\left[\,\displaystyle \frac{\,1\,}{\,4\,}x^{2}\,\right]_{0}^{1}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}
\end{eqnarray}\)
確率 \( P(\,1{\small ~≦~}X{\small ~≦~}2\,) \) は、以下の面積となるので、
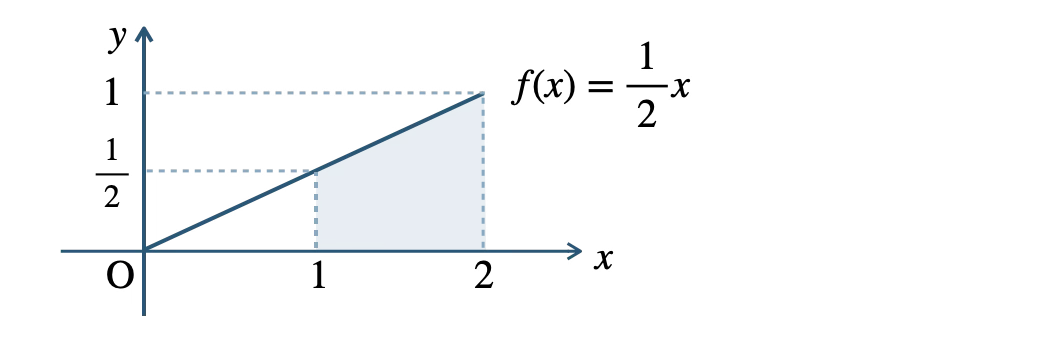
\(0{\small ~≦~}X{\small ~≦~}2\) の範囲全体の面積は \(1\) より、
\(\begin{eqnarray}~~~P(\,1{\small ~≦~}X{\small ~≦~}2\,)&=&1-P(\,0{\small ~≦~}X{\small ~≦~}1\,)
\\[5pt]~~~&=&1-\displaystyle \frac{\,1\,}{\,4\,}
\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,4\,}
\end{eqnarray}\)
【別解】積分を用いると、
\(\begin{eqnarray}~~~\displaystyle \int_{1}^{2}\displaystyle \frac{\,1\,}{\,2\,}x\,dx&=&\left[\,\displaystyle \frac{\,1\,}{\,4\,}x^{2}\,\right]_{1}^{2}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}(4-1)
\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,4\,}
\end{eqnarray}\)



