- 数学B|統計的な推測「文字係数の確率密度関数」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|文字係数の確率密度関数
\(\displaystyle f(x)=\begin{cases}
\,ax\, & (\,0{\small ~≦~}x{\small ~≦~}2\,)\\[3pt]
\,a(4-x)\, & (\,2{\small ~≦~}x{\small ~≦~}4\,)
\end{cases}\)
であるとき、定数 \(a\) の値の求め方は?また、確率 \(P(\,1{\small ~≦~}X{\small ~≦~}3\,)\) の求め方は?
高校数学B|統計的な推測
解法のPoint
文字係数の確率密度関数
文字係数の確率密度関数の定数の求め方は、
① 確率変数 \(X\) のとる値の範囲 \(\alpha{\small ~≦~}X{\small ~≦~}\beta\) での \(y=f(x)\) が \(x\) 軸で囲まれる面積が \(1\) になる定積分の式を立てる。
\(\begin{eqnarray}~~~\displaystyle \int_{\alpha}^{\beta} f(x)\,dx &=& 1
\end{eqnarray}\)
② 定積分の式を方程式として解き、定数の値を求める。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|文字係数の確率密度関数
確率変数 \(X\) が \(0{\small ~≦~}X{\small ~≦~}4\) の範囲をとり、確率密度関数が
\(\displaystyle f(x)=\begin{cases}
\,ax\, & (\,0{\small ~≦~}x{\small ~≦~}2\,)\\[3pt]
\,a(4-x)\, & (\,2{\small ~≦~}x{\small ~≦~}4\,)
\end{cases}\)
であるとき、定数 \(a\) の値の求め方は?また、確率 \(P(\,1{\small ~≦~}X{\small ~≦~}3\,)\) の求め方は?
高校数学B|統計的な推測
確率密度関数は、
\(~~~\displaystyle f(x)=\begin{cases}
\,ax\, & (\,0{\small ~≦~}x{\small ~≦~}2\,)\\[3pt]
\,a(4-x)\, & (\,2{\small ~≦~}x{\small ~≦~}4\,)
\end{cases}\)
これより、\(0{\small ~≦~}X{\small ~≦~}4\) の範囲での確率は \(\displaystyle \int_{0}^{4} f(x)\,dx = 1\) であるので、
\(\begin{eqnarray}~~~
\displaystyle \int_{0}^{2} a x\,dx+\int_{2}^{4} a(4-x)\,dx = 1\end{eqnarray}\) \(~~~\cdots \small [\,1\,]\)
ここで、
\(\begin{eqnarray}~~~\displaystyle \int_{0}^{2} a x\,dx &=& a\left[ \displaystyle \frac{\,1\,}{\,2\,}x^{2} \right]_{0}^{2}\\[5pt]
&=& a\cdot \displaystyle \frac{\,1\,}{\,2\,}\cdot 2^{2} = 2a
\end{eqnarray}\)
また、
\(\begin{eqnarray}~~~\displaystyle \int_{2}^{4} a(4-x)\,dx &=& a\left[ 4x-\displaystyle \frac{\,1\,}{\,2\,}x^{2} \right]_{2}^{4}\\[5pt]
&=& a\left\{(16-8)-(8-2)\right\}\\[5pt]
&=& a(8-6) = 2a
\end{eqnarray}\)
よって、\(\small [\,1\,]\) に代入して、
\(\begin{eqnarray}~~~2a+2a&=&1\\[5pt]
4a&=&1\\[5pt]
a&=&\displaystyle \frac{\,1\,}{\,4\,}
\end{eqnarray}\)
\(a=\displaystyle \frac{\,1\,}{\,4\,}\) のとき、確率密度関数は、
\(~~~\displaystyle f(x)=\begin{cases}
\,\displaystyle \frac{\,1\,}{\,4\,}x\, & (\,0{\small ~≦~}x{\small ~≦~}2\,)\\[5pt]
\,\displaystyle \frac{\,1\,}{\,4\,}(4-x)\, & (\,2{\small ~≦~}x{\small ~≦~}4\,)
\end{cases}\)
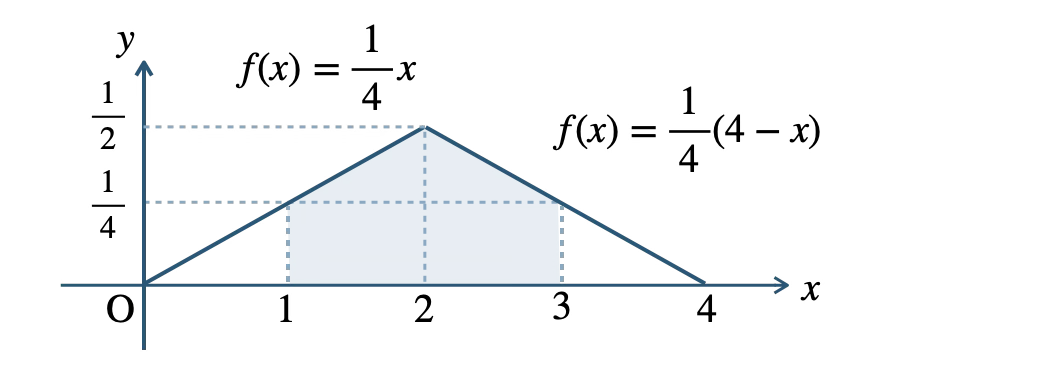
これより、確率 \(P(\,1{\small ~≦~}X{\small ~≦~}3\,)\) は、
対称性より、\(1{\small ~≦~}X{\small ~≦~}2\) の範囲の面積の \(2\) 倍となるので、
\(\begin{split}&P(\,1{\small ~≦~}X{\small ~≦~}3\,)
\\[5pt]~~=~&2\left( \displaystyle \frac{\,1\,}{\,2\,}\cdot 2\cdot \displaystyle \frac{\,1\,}{\,2\,}-\displaystyle \frac{\,1\,}{\,2\,}\cdot 1\cdot \displaystyle \frac{\,1\,}{\,4\,}\right)
\\[5pt]~~=~&2\left( \displaystyle \frac{\,1\,}{\,2\,}-\displaystyle \frac{\,1\,}{\,8\,}\right)
\\[5pt]~~=~&2\cdot \displaystyle \frac{\,4-1\,}{\,8\,}
\\[5pt]~~=~&\displaystyle \frac{\,3\,}{\,4\,}
\end{split}\)
【別解】積分を用いると、
\(\begin{split}&P(\,1{\small ~≦~}X{\small ~≦~}3\,)
\\[5pt]~~=~&\displaystyle \int_{1}^{2} \frac{\,1\,}{\,4\,}x\,dx +\int_{2}^{3} \frac{\,1\,}{\,4\,}(4-x)\,dx
\\[5pt]~~=~&\displaystyle \frac{\,1\,}{\,4\,}\left[ \frac{\,1\,}{\,2\,}x^{2} \right]_{1}^{2} +\frac{\,1\,}{\,4\,}\left[ 4x-\frac{\,1\,}{\,2\,}x^{2} \right]_{2}^{3}
\\[5pt]~~=~&\displaystyle \frac{\,1\,}{\,8\,}(4-1) +\frac{\,1\,}{\,4\,}\left\{\left(12-\frac{\,9\,}{\,2\,}\right)-(8-2)\right\}
\\[5pt]~~=~&\displaystyle \frac{\,3\,}{\,8\,} +\frac{\,1\,}{\,4\,}\cdot \frac{\,3\,}{\,2\,}
\\[5pt]~~=~&\displaystyle \frac{\,3\,}{\,8\,} +\frac{\,3\,}{\,8\,} = \frac{\,3\,}{\,4\,}
\end{split}\)



