- 数学B|統計的な推測「正規分布の度数を求める文章問題」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|正規分布の度数を求める文章問題
統計的な推測 32☆あるクラスの男子の身長が、平均 \( 170 ~{\rm cm}\)、標準偏差 \( 3 ~{\rm cm}\) の正規分布に従い、身長 \( 173 ~{\rm cm}\) 以上の生徒が \(4\) 人いたとき、このクラスの男子は約何人であるか?ただし、\( p(1)=0.3413 \) とする。
高校数学B|統計的な推測
解法のPoint
正規分布の度数を求める文章問題
Point:正規分布の度数を求める文章問題
① 文章より、確率変数 \( X \) の期待値(平均) \( m \)、標準偏差 \( \sigma \) と確率変数の範囲を読み取る。
\( m=170 ~,~ \sigma=3 ~,~ P(\,X{\small ~≧~}173\,) \)
② 変換式より、標準正規分布に従う \(Z\) に変換し、正規分布表より確率を求める。
\(\begin{eqnarray}~~~Z=\displaystyle \frac{\,X-170\,}{\,3\,}\end{eqnarray}\) より、
\( P(\,Z{\small ~≧~}1\,)=0.1587 \)
③ 割合の式より、全体の人数を求める。
全体の人数 × 確率 = 基準値の人数より、
\(\begin{eqnarray}~~~x {\, \small \times \,} 0.1587&=&4
\\[3pt]~~~x&{\small ~≒~}&25
\end{eqnarray}\)
基準値を満たす人数から、全体の人数を求める問題は、
① 文章より、確率変数 \( X \) の期待値(平均) \( m \)、標準偏差 \( \sigma \) と確率変数の範囲を読み取る。
\( m=170 ~,~ \sigma=3 ~,~ P(\,X{\small ~≧~}173\,) \)
② 変換式より、標準正規分布に従う \(Z\) に変換し、正規分布表より確率を求める。
\(\begin{eqnarray}~~~Z=\displaystyle \frac{\,X-170\,}{\,3\,}\end{eqnarray}\) より、
\( P(\,Z{\small ~≧~}1\,)=0.1587 \)
③ 割合の式より、全体の人数を求める。
全体の人数 × 確率 = 基準値の人数より、
\(\begin{eqnarray}~~~x {\, \small \times \,} 0.1587&=&4
\\[3pt]~~~x&{\small ~≒~}&25
\end{eqnarray}\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|正規分布の度数を求める文章問題
統計的な推測 32☆
あるクラスの男子の身長が、平均 \( 170 ~{\rm cm}\)、標準偏差 \( 3 ~{\rm cm}\) の正規分布に従い、身長 \( 173 ~{\rm cm}\) 以上の生徒が \(4\) 人いたとき、このクラスの男子は約何人であるか?ただし、\( p(1)=0.3413 \) とする。
高校数学B|統計的な推測
身長 \( X~{\rm cm}\) を確率変数とし、\( m=170~,~\sigma=3 \) より、確率変数 \(X\) は正規分布 \( N(170~,~3^2) \) に従う
よって、\( Z=\displaystyle \frac{\,X-m\,}{\,\sigma\,} \) とおくと、
確率変数 \( Z \) は標準正規分布 \( N(0~,~1) \) に従う
ここで、\( X=173 \) のとき、
\(\begin{eqnarray}~~~Z&=&\displaystyle \frac{\,173-170\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,3\,}=1
\end{eqnarray}\)
これより、確率変数 \( Z \) に変換すると、
\(\begin{eqnarray}~~~P(X{\small ~≧~}173)&=&P(Z{\small ~≧~}1)
\\[5pt]~~~&=&0.5-p(1)
\\[5pt]~~~&=&0.5-0.3413
\\[5pt]~~~&=&0.1587
\end{eqnarray}\)
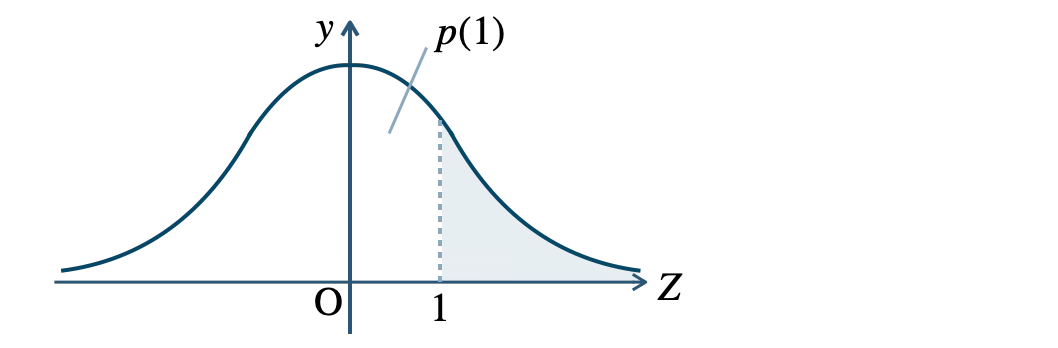

このクラスの男子の人数を \( x \) とすると、\( 173~{\rm cm} \) 以上の生徒が \( 4 \) 人であるので、
\(\begin{eqnarray}~~~x{\, \small \times \,}0.1587&=&4
\\[5pt]~~~x&=&\displaystyle \frac{\,4\,}{\,0.1587\,}{\small ~≒~}25.20\cdots
\end{eqnarray}\)
したがって、約 \( 25 \) 人となる



