- 数学B|統計的な推測「標本平均と正規分布」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|標本平均と正規分布
統計的な推測 40母平均 \( 50 \) 、母標準偏差 \( 30 \) の母集団から大きさ \( 100 \) の標本を無作為抽出するとき、その標本平均が \( 53 \) より大きい値をとる確率の求め方は?ただし、\( p(1)=0.3413 \) とする。
高校数学B|統計的な推測
解法のPoint
標本平均と正規分布
Point:標本平均と正規分布
① 母平均と母標準偏差から、標本平均の期待値(平均)と標準偏差を求める。
期待値(平均) \( E(\overline{X})=m=50\)
標準偏差 \(\sigma(\overline{X})=\displaystyle \frac{\,\sigma\,}{\,\sqrt{n}\,}=\displaystyle \frac{\,30\,}{\,\sqrt{100}\,}=3\)
② 標本平均 \( \overline{X} \) は正規分布 \( N\left(m~,~\displaystyle \frac{\,\sigma^{2}\,}{\,n\,}\right) \) に従うので、\( \overline{X} \) を \( Z \) に変換して標準正規分布 \( N(0,1) \) に従うとする。
\( Z=\displaystyle \frac{\,\overline{X}-m\,}{\,\displaystyle \frac{\,\sigma\,}{\,\sqrt{n}\,}\,}=\displaystyle \frac{\,\overline{X}-50\,}{\,3\,} \) より、
\(\overline{X}=53 \) のとき、\(Z=1\)
③ 正規分布の表より、確率を求める。
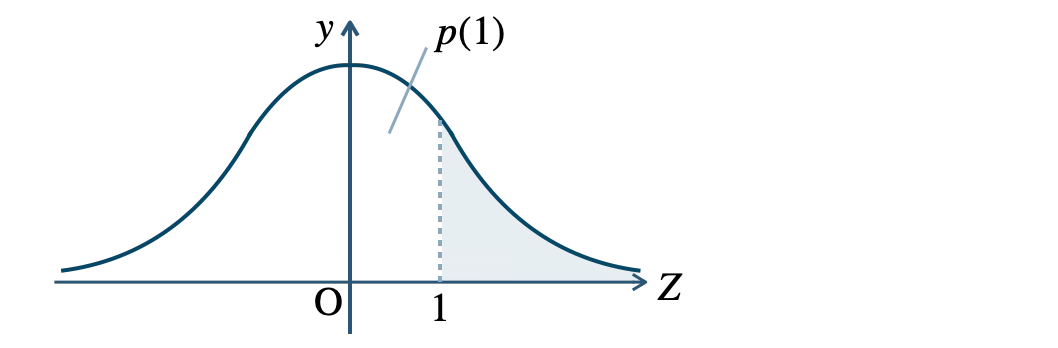
\(P(\,\overline{X}{\small ~≧~}53\,)=P\left(Z{\small ~≧~}1\right)=0.5-p(1)\)
母平均 \( m=50 \) 、母標準偏差 \( \sigma=30 \) の母集団から、大きさ \( n=100 \) の標本を無作為抽出するときの標本平均 \( \overline{X} \) の取る値についての確率は、
① 母平均と母標準偏差から、標本平均の期待値(平均)と標準偏差を求める。
期待値(平均) \( E(\overline{X})=m=50\)
標準偏差 \(\sigma(\overline{X})=\displaystyle \frac{\,\sigma\,}{\,\sqrt{n}\,}=\displaystyle \frac{\,30\,}{\,\sqrt{100}\,}=3\)
② 標本平均 \( \overline{X} \) は正規分布 \( N\left(m~,~\displaystyle \frac{\,\sigma^{2}\,}{\,n\,}\right) \) に従うので、\( \overline{X} \) を \( Z \) に変換して標準正規分布 \( N(0,1) \) に従うとする。
\( Z=\displaystyle \frac{\,\overline{X}-m\,}{\,\displaystyle \frac{\,\sigma\,}{\,\sqrt{n}\,}\,}=\displaystyle \frac{\,\overline{X}-50\,}{\,3\,} \) より、
\(\overline{X}=53 \) のとき、\(Z=1\)
③ 正規分布の表より、確率を求める。
\(P(\,\overline{X}{\small ~≧~}53\,)=P\left(Z{\small ~≧~}1\right)=0.5-p(1)\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|標本平均と正規分布
統計的な推測 40
母平均 \( 50 \) 、母標準偏差 \( 30 \) の母集団から大きさ \( 100 \) の標本を無作為抽出するとき、その標本平均が \( 53 \) より大きい値をとる確率の求め方は?ただし、\( p(1)=0.3413 \) とする。
高校数学B|統計的な推測
母平均 \( m=50 \) 、母標準偏差 \( \sigma=30 \) より、
標本平均 \( \overline{X} \) の期待値(平均)は母平均と等しいので、
\( E(\overline{X})=m=50 \)
標準偏差は、母標準偏差を標本の大きさの平方根で割った値となるので、
\(\begin{eqnarray}~~~\sigma(\overline{X})&=&\displaystyle \frac{\,30\,}{\,\sqrt{100}\,}
\\[5pt]~~~&=&\displaystyle \frac{\,30\,}{\,10\,}=3
\end{eqnarray}\)
ここで、標本の大きさが大きいので、
標本平均 \( \overline{X} \) は 正規分布 \( N\left(50~,~3^2\right) \) に従う
よって、変換の式 \( Z=\displaystyle \frac{\,\overline{X}-50\,}{\,3\,} \) より、
確率変数 \(Z\) は 標準正規分布 \( N(0~,~1) \) に従う
\( \overline{X}=53 \) のとき
\(\begin{eqnarray}~~~Z&=&\displaystyle \frac{\,53-50\,}{\,3\,}=\displaystyle \frac{\,3\,}{\,3\,}=1
\end{eqnarray}\)
よって、標本平均が \( 53 \) より大きい値をとる確率は、
\(\begin{eqnarray}~~~P(\,\overline{X}{\small ~≧~}53\,)&=&P(\,Z{\small ~≧~}1\,)
\\[5pt]~~~&=&0.5-p(1)
\\[5pt]~~~&=&0.5-0.3413
\\[5pt]~~~&=&0.1587
\end{eqnarray}\)