- 数学B|統計的な推測「母比率の信頼区間の幅」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|母比率の信頼区間の幅
統計的な推測 47☆ある意見に対する賛成率が約 \(60\) %と予想されており、この意見に対する賛成率を信頼度 \(95\) %で信頼区間の幅が \(8\) %以下になるように推定したいとき、何人以上を抽出して調べればよいか?
高校数学B|統計的な推測
解法のPoint
母比率の信頼区間の幅
Point:母比率の信頼区間の幅
\(E_p=1.96\cdot\sqrt{\displaystyle \frac{\,R(1-R)\,}{\,n\,}}\) とおくと、
母比率 \( p \) に対する信頼度 \(95\) %の信頼区間は、
\(\begin{eqnarray}\left[\,R-E_p~,~R+E_p\,\right]\end{eqnarray}\)
これより、信頼区間の幅は、
\(2E_p=2{\, \small \times \,}1.96\cdot \sqrt{\displaystyle \frac{\,R(1-R)\,}{\,n\,}}\)
母比率 \( p \) の母集団から大きさ \( n \) の標本を無作為に抽出し、標本比率が \( R \) となるとき、
\( n \) が大きければ、
\(E_p=1.96\cdot\sqrt{\displaystyle \frac{\,R(1-R)\,}{\,n\,}}\) とおくと、
母比率 \( p \) に対する信頼度 \(95\) %の信頼区間は、
\(\begin{eqnarray}\left[\,R-E_p~,~R+E_p\,\right]\end{eqnarray}\)
これより、信頼区間の幅は、
\(2E_p=2{\, \small \times \,}1.96\cdot \sqrt{\displaystyle \frac{\,R(1-R)\,}{\,n\,}}\)
で表される。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|母比率の信頼区間の幅
統計的な推測 47☆
ある意見に対する賛成率が約 \(60\) %と予想されており、この意見に対する賛成率を信頼度 \(95\) %で信頼区間の幅が \(8\) %以下になるように推定したいとき、何人以上を抽出して調べればよいか?
高校数学B|統計的な推測
標本比率を \( R \)、標本の大きさを \( n \) とすると、
\(n\) が大きいとき、標本比率 \(R\) は母比率 \( 0.6 \) に近づくと考えられる
よって、信頼度 \(95\%\) の信頼区間の幅は、
\(\begin{eqnarray}~~~2E_p&=&2{\, \small \times \,} 1.96\cdot \sqrt{ \displaystyle \frac{\,R(1-R)\,}{\,n\,} }
\\[5pt]~~~&=&2{\, \small \times \,} 1.96\cdot \sqrt{ \displaystyle \frac{\,0.6\cdot 0.4\,}{\,n\,} }
\end{eqnarray}\)
これが \(0.08\) 以下となるので、
\(\begin{eqnarray}~~~2\cdot 1.96\cdot \sqrt{ \displaystyle \frac{\,0.6\cdot 0.4\,}{\,n\,} }&{\small ~≦~}&0.08
\\[5pt]~~~2\cdot 1.96\cdot \displaystyle \frac{\,\sqrt{ 0.6\cdot 0.4}\,}{\,\sqrt{ n}\,}
&{\small ~≦~}&0.08
\\[5pt]~~~2\cdot 1.96\cdot \sqrt{\displaystyle \frac{\,6\,}{\,10\,}\cdot \displaystyle \frac{\,4\,}{\,10\,}}&{\small ~≦~}&0.08\sqrt{n}
\\[5pt]~~~2\cdot 1.96\cdot \displaystyle \frac{\,\sqrt{24}\,}{\,10\,}&{\small ~≦~}&\displaystyle \frac{\,8\,}{\,100\,}\sqrt{n}
\\[5pt]~~~2\cdot 1.96\cdot \displaystyle \frac{\,2\sqrt{6}\,}{\,10\,}\cdot \displaystyle \frac{\,100\,}{\,8\,}&{\small ~≦~}&\sqrt{n}
\\[5pt]~~~9.8\cdot \sqrt{6}&{\small ~≦~}&\sqrt{n}
\\[5pt]~~~\sqrt{n}&{\small ~≧~}&9.8\cdot \sqrt{6}
\end{eqnarray}\)
両辺を2乗すると、
\(\begin{eqnarray}\hspace{20pt}~~~n&{\small ~≧~}&96.04\cdot 6
\\[5pt]~~~n&{\small ~≧~}&576.24
\end{eqnarray}\)
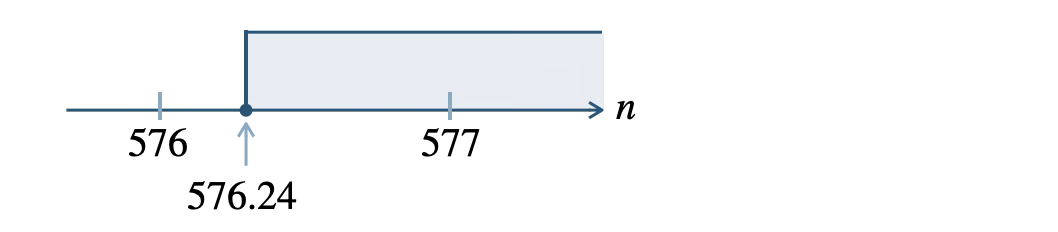

したがって、\(577\) 人以上を抽出すればよい



