- 数学B|統計的な推測「母比率の仮説検定(片側検定1%)」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|母比率の仮説検定(片側検定1%)
高校数学B|統計的な推測
・数研出版の教科書→棄却域タイプ
・問題集など→正規分布表タイプ
・東京書籍の教科書→標本比率タイプ
母比率の仮説検定(片側検定1%)|棄却域タイプ
解法のPoint|棄却域タイプ
① 判断したい説に反する仮説を立てる。
不良品率が下がった(判断したい)
(仮説)不良品率が下がっていない \(p=0.1\)
② 仮説が正しいとして、確率変数 \( X \) の期待値(平均)と標準偏差を求めて、標準正規分布に従う \( Z \) に変換する。
\( n=900 \) が大きいとき、
二項分布 \( B(900~,~0.1) \) より、
\(m=n\,p=90\)
\(\sigma=\sqrt{\,n\,p\,(1-p)\,}=9\)
変換の式は、\(Z=\displaystyle \frac{\,X-m\,}{\,\sigma\,}=\displaystyle \frac{\,X-90\,}{\,9\,}\)
③ 有意水準より棄却域を求める。
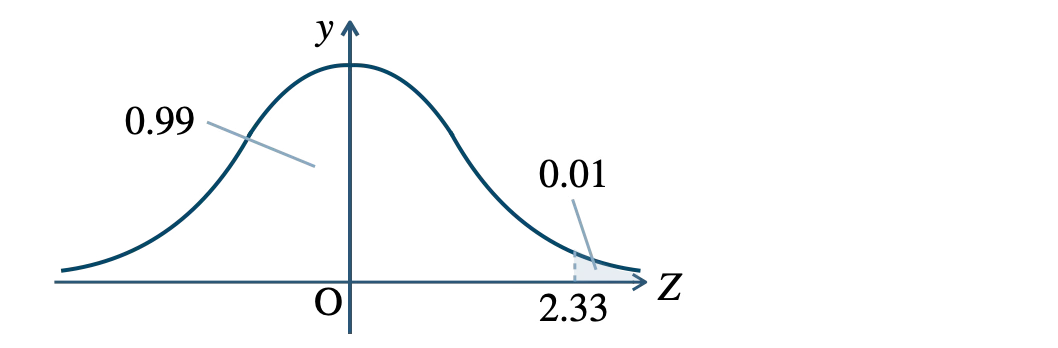

\( P(\,0{\small ~≦~}Z{\small ~≦~}2.33\,){\small ~≒~}0.49 \) より、
有意水準 \( 1 \) %の片側検定の棄却域は、
・上がったか判定 \(Z{\small ~≧~}2.33\)
・下がったか判定 \(Z{\small ~≦~}-2.33\)
④ \(X\) の値を \(Z\) に変換して、\(Z\) の値が棄却域に入るかどうかを調べる。
棄却域に入る(めったに起こらない事象)
→ 下がっていないという仮説を棄却
→ 下がったと判断できる
棄却域に入らない(十分起こりうる事象)
→ 下がっていないという仮説を棄却できない
→ 下がったと判断できない
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|棄却域タイプ
ある製品の不良品率が \( 10 \) %であったが、新たに開発した製品から \(900\) 個を無作為に抽出し調べると不良品は \(72\) 個であったとき、不良品率が下がったと判断しても良いか有意水準 \( 1 \) %で検定する方法は?ただし、\( P(\,0{\small ~≦~}Z{\small ~≦~}2.33\,){\small ~≒~}0.49~,~\)\(p(2)=0.4772 \) とする。
高校数学B|統計的な推測
不良品率が下がったと判断したいので、
不良品率が下がっていない \(p=0.1\) と仮説を立てる
仮説が正しいとすると、\(900\) 個中不良品である個数 \(X\) は、二項分布 \(B(900~,~0.1)\) に従う
よって、確率変数 \(X\) の期待値(平均)と標準偏差は、
\(~~~m=900{\, \small \times \,}0.1=90\)
\(\begin{eqnarray}~~~\sigma&=&\sqrt{\,900{\, \small \times \,}0.1\cdot(1-0.1)\,}
\\[5pt]~~~&=&\sqrt{81}=9
\end{eqnarray}\)
これより、確率変数 \(X\) は近似的に正規分布 \(N(90~,~9^2)\) に従う
また、\(Z=\displaystyle \frac{\,X-90\,}{\,9\,}~~~\cdots {\small [\,1\,]}\) とおくと、
確率変数 \(Z\) は標準正規分布 \(N(0~,~1)\) に従う
ここで、\( P(\,0{\small ~≦~}Z{\small ~≦~}2.33\,){\small ~≒~}0.49 \) より、
不良品率が下がった判定の有意水準 \(1\) %の棄却域は、
\(~~~Z{\small ~≦~}-2.33 ~ ~ ~\cdots {\small [\,2\,]}\)
\(X=72\) のとき、\({\small [\,1\,]}\) より、
\(\begin{eqnarray}~~~Z&=&\displaystyle \frac{\,72-90\,}{\,9\,}
=\displaystyle \frac{\,-18\,}{\,9\,}=-2.0
\end{eqnarray}\)
これは \({\small [\,2\,]}\) の棄却域に入らないので、仮説を棄却できない
したがって、不良品率が下がったと判断できない
練習問題アーカイブページはこちら→
母比率の仮説検定(片側検定1%)
母比率の仮説検定(片側検定1%)|正規分布表タイプ
解法のPoint|正規分布表タイプ
① 判断したい説に反する仮説を立てる。
不良品率が下がった(判断したい)
(仮説)不良品率が下がっていない \(p=0.1\)
② 仮説が正しいとして、確率変数 \( X \) の期待値(平均)と標準偏差を求めて、標準正規分布に従う \( Z \) に変換する。
\( n=900 \) が大きいとき、
二項分布 \( B(900~,~0.1) \) より、
\(m=n\,p=90\)
\(\sigma=\sqrt{\,n\,p\,(1-p)\,}=9\)
変換の式は、\(Z=\displaystyle \frac{\,X-m\,}{\,\sigma\,}=\displaystyle \frac{\,X-90\,}{\,9\,}\)
③ \(X\) の値から \(Z\) を求めて、確率変数 \(Z\) がその値以上となる確率を求める。
\(X=72\) のとき、\(Z=-2.0\)
よって、正規分布表より、
\(P\left(Z{\small ~≦~}-2.0\right)=0.0228\)
④ 求めた確率と有意水準 \( 1 \) %を比較する。
・ 求めた確率が有意水準 \( 1 \) %より小さい
→ めったに起こらない事象が起こる
→ 下がっていないという仮説を棄却
→ 下がったと判断できる
・ 求めた確率が有意水準 \( 1 \) %より大きい
→ 十分起こりうる事象が起こる
→ 下がっていないという仮説を棄却できない
→ 下がったと判断できない
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|正規分布表タイプ
ある製品の不良品率が \( 10 \) %であったが、新たに開発した製品から \(900\) 個を無作為に抽出し調べると不良品は \(72\) 個であったとき、不良品率が下がったと判断しても良いか有意水準 \( 1 \) %で検定する方法は?ただし、\( P(\,0{\small ~≦~}Z{\small ~≦~}2.33\,){\small ~≒~}0.49~,~\)\(p(2)=0.4772 \) とする。
高校数学B|統計的な推測
不良品率が下がったと判断したいので、
不良品率が下がっていない \(p=0.1\) と仮説を立てる
仮説が正しいとすると、\(900\) 個中不良品である個数 \(X\) は、二項分布 \(B(900~,~0.1)\) に従う
よって、確率変数 \(X\) の期待値(平均)と標準偏差は、
\(~~~m=900{\, \small \times \,}0.1=90\)
\(\begin{eqnarray}~~~\sigma&=&\sqrt{\,900{\, \small \times \,}0.1\cdot(1-0.1)\,}
\\[5pt]~~~&=&\sqrt{81}=9
\end{eqnarray}\)
これより、確率変数 \(X\) は近似的に正規分布 \(N(90~,~9^2)\) に従う
また、\(Z=\displaystyle \frac{\,X-90\,}{\,9\,}~~~\cdots {\small [\,1\,]}\) とおくと、
確率変数 \(Z\) は標準正規分布 \(N(0~,~1)\) に従う
\(X=72\) のとき、\({\small [\,1\,]}\) より、
\(\begin{eqnarray}~~~Z&=&\displaystyle \frac{\,72-90\,}{\,9\,}
=\displaystyle \frac{\,-18\,}{\,9\,}=-2.0
\end{eqnarray}\)
よって、確率変数 \(Z\) が \(-2.0\) 以下となる確率は、
正規分布表より、\(p(2.0)=0.4772\) を用いて、
\(\begin{eqnarray}P\left(Z{\small ~≦~}-2.0\right)&=&0.5-p(2.0)
\\[3pt]~~&=&0.5-0.4772
\\[3pt]~~&=&0.0228
\end{eqnarray}\)
よって、\(2.28\) %となり、有意水準 \(1\) %よりも大きくなり、仮説を棄却できない
したがって、不良品率が下がったと判断できない
母比率の仮説検定(片側検定1%)|標本比率タイプ
解法のPoint|標本比率タイプ
① 帰無仮説と対立仮説を立てる。
不良品率が下がっていないを帰無仮説 \(p=0.1\)
不良品率が下がったを対立仮説 \(p\lt 0.1\)
② 帰無仮説が正しいとして、標本比率 \(p^{\prime}\) より、標準正規分布に従う \( Z \) に変換する。
期待値(平均)は、\(E(p^{\prime})=p=0.1\)
標準偏差は、\(\sigma(p^{\prime})=\sqrt{\,\displaystyle \frac{\,p(1-p)\,}{\,n\,}}=0.01\)
変換の式は、\(Z=\displaystyle \frac{\,p^{\prime}-p\,}{\,\sigma(p^{\prime})\,}\)
③ \(X\) の値から標本比率 \(p^{\prime}\) を求めて、母比率 \(p\) との差を求める。
\(X=72\) のとき、\(p^{\prime}=\displaystyle \frac{\,X\,}{\,n\,}=0.08\)
よって、\(p^{\prime}-p=-0.02\)
④ 標本比率と母比率の差が③の値以下となる確率を求める。
\(p^{\prime}-p{\small ~≦~}-0.02\) より、
\(\begin{eqnarray}~~~\displaystyle \frac{\,p^{\prime}-p\,}{\,\sigma(p^{\prime})\,}
&{\small ~≦~}&
\displaystyle \frac{\,-0.02\,}{\,\sigma(p^{\prime})\,}
\end{eqnarray}\)
これより、
\(\begin{split}&P\left(\,p^{\prime}-p{\small ~≦~}-0.02\,\right)
\\[5pt]~~=~&P\left(Z{\small ~≦~}-2.0\right)=0.0228\end{split}\)
⑤ 求めた確率と有意水準 \( 1 \) %を比較する。
・ 求めた確率が有意水準 \( 1 \) %より小さい
→ めったに起こらない事象が起こる
→ 下がっていないという帰無仮説を棄却
→ 下がったと判断できる
・ 求めた確率が有意水準 \( 1 \) %より大きい
→ 十分起こりうる事象が起こる
→ 下がっていないという帰無仮説を棄却できない
→ 下がったと判断できない
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|標本比率タイプ
ある製品の不良品率が \( 10 \) %であったが、新たに開発した製品から \(900\) 個を無作為に抽出し調べると不良品は \(72\) 個であったとき、不良品率が下がったと判断しても良いか有意水準 \( 1 \) %で検定する方法は?ただし、\( P(\,0{\small ~≦~}Z{\small ~≦~}2.33\,){\small ~≒~}0.49~,~\)\(p(2)=0.4772 \) とする。
高校数学B|統計的な推測
不良品率を \( p \) とすると、
帰無仮説は、\( p=0.1 \)
対立仮説は、\( p\lt 0.1 \)
また、標本比率を \( p^{\prime} \) とすると、
期待値(平均)は、
\(~~~E(p^{\prime})=p=0.1\)
標準偏差は、
\(\begin{eqnarray}~~~\sigma(p^{\prime})&=&\sqrt{\,\displaystyle \frac{\,p(1-p)\,}{\,n\,}}
\\[5pt]~~~&=&\sqrt{\,\displaystyle \frac{\,0.1\cdot (1-0.1)\,}{\,900\,}}
\\[5pt]~~~&=&\sqrt{\,\displaystyle \frac{\,0.1\cdot 0.9\,}{\,900\,}}
\\[5pt]~~~&=&\sqrt{\,\displaystyle \frac{\,0.01\,}{\,100\,}}
\\[5pt]~~~&=&\displaystyle \frac{\,0.1\,}{\,10\,}
\\[5pt]~~~&=&0.01
\end{eqnarray}\)
\( Z=\displaystyle \frac{\,p^{\prime}-p\,}{\,\sigma(p^{\prime})\,} \) とおくと、
確率変数 \( Z \) は標準正規分布 \(N(0~,~1)\) に従う
\(X=72\) のとき、標本比率 \( p^{\prime} \) は、
\(\begin{eqnarray}~~~p^{\prime}&=&\displaystyle \frac{\,X\,}{\,n\,}=\displaystyle \frac{\,72\,}{\,900\,}=0.08
\end{eqnarray}\)
ここで、標本比率と母比率の差が \( -0.02 \) 以下となる確率を考えると、
\(~~~p^{\prime}-p{\small ~≦~}-0.02\)
両辺を \( \sigma(p^{\prime}) \) で割ると、
\(\begin{eqnarray}~~~\displaystyle \frac{\,p^{\prime}-p\,}{\,\sigma(p^{\prime})\,}
&{\small ~≦~}&
\displaystyle \frac{\,-0.02\,}{\,\sigma(p^{\prime})\,}
\end{eqnarray}\)
左辺は \( Z \) となり、右辺は \( \sigma(p^{\prime})=0.01\) より、
\(\begin{eqnarray}~~~Z&{\small ~≦~}&\displaystyle \frac{\,-0.02\,}{\,0.01\,}
\\[5pt]~~~Z&{\small ~≦~}&-2.0
\end{eqnarray}\)
よって、確率変数 \(Z\) が \(-2.0\) 以下となる確率は、
正規分布表より、\(p(2.0)=0.4772\) を用いて、
\(\begin{eqnarray}P\left(Z{\small ~≦~}-2.0\right)&=&0.5-p(2.0)
\\[3pt]~~&=&0.5-0.4772
\\[3pt]~~&=&0.0228
\end{eqnarray}\)
よって、\(2.28\) %となり、有意水準 \(1\) %よりも大きくなり、帰無仮説 \(p=0.1\) を棄却できない
したがって、不良品率が下がったと判断できない



