- 数学C|平面上のベクトル「ベクトルの和の表し方」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|ベクトルの和の表し方
平面上のベクトル 02平面上の2つのベクトル \(\overrightarrow{a}~,~ \overrightarrow{b}\) の和 \(\overrightarrow{a}+\overrightarrow{b}\) の図示の方法は?(2通り)
高校数学C|平面上のベクトル
解法のPoint
ベクトルの和の表し方
Point:ベクトルの和の表し方
■ 順番に終点と始点をつなげる


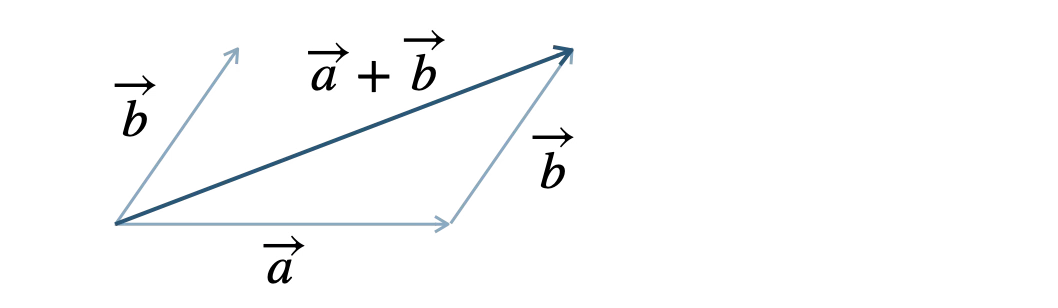
① \( \overrightarrow{b} \) を平行移動させ、\( \overrightarrow{a} \) の終点と \( \overrightarrow{b} \) の始点を揃える。
② \( \overrightarrow{a} \) の始点と \( \overrightarrow{b} \) の終点をつなげたベクトルが \( \overrightarrow{a}+\overrightarrow{b} \) である。


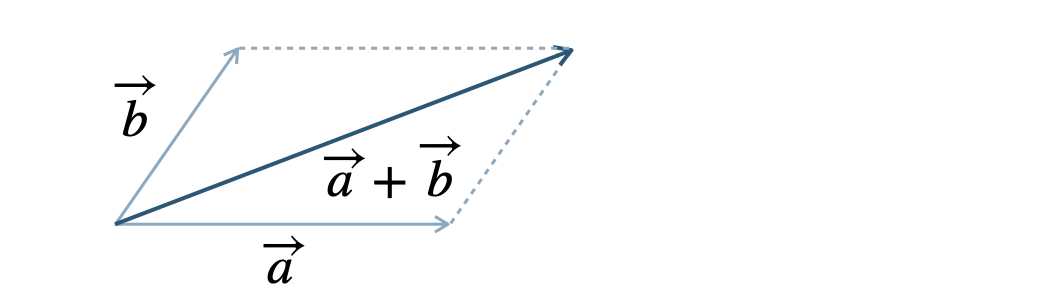
① 始点をそろえた \( \overrightarrow{a} \) と \( \overrightarrow{b} \) を隣り合う2辺とする平行四辺形を作る。
② 平行四辺形の対角線のベクトルが \( \overrightarrow{a}+\overrightarrow{b} \) である。
交換法則 \( \overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a} \)
結合法則 \( (\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c}) \)
2つのベクトルの和の表し方は、
■ 順番に終点と始点をつなげる



① \( \overrightarrow{b} \) を平行移動させ、\( \overrightarrow{a} \) の終点と \( \overrightarrow{b} \) の始点を揃える。
② \( \overrightarrow{a} \) の始点と \( \overrightarrow{b} \) の終点をつなげたベクトルが \( \overrightarrow{a}+\overrightarrow{b} \) である。
■ 平行四辺形の対角線



① 始点をそろえた \( \overrightarrow{a} \) と \( \overrightarrow{b} \) を隣り合う2辺とする平行四辺形を作る。
② 平行四辺形の対角線のベクトルが \( \overrightarrow{a}+\overrightarrow{b} \) である。
ベクトルの加法には、次の法則が成り立つ。
交換法則 \( \overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a} \)
結合法則 \( (\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c}) \)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|ベクトルの和の表し方
平面上のベクトル 02
平面上の2つのベクトル \(\overrightarrow{a}~,~ \overrightarrow{b}\) の和 \(\overrightarrow{a}+\overrightarrow{b}\) の図示の方法は?(2通り)
高校数学C|平面上のベクトル
\(\small [\,1\,]\) 始点のそろった2つのベクトル \( \overrightarrow{a} \,\,,\, \overrightarrow{b} \) について、
\( \overrightarrow{b} \) を平行移動させ、\( \overrightarrow{a} \) の終点と \( \overrightarrow{b} \) の始点を揃える
\( \overrightarrow{a} \) の始点と \( \overrightarrow{b} \) の終点をつなげたベクトルが \( \overrightarrow{a}+\overrightarrow{b} \) である



\(\small [\,2\,]\) 始点のそろった2つのベクトル \( \overrightarrow{a} \,\,,\, \overrightarrow{b} \) について、
\( \overrightarrow{a} \) と \( \overrightarrow{b} \) を隣り合う2辺とする平行四辺形を作る
平行四辺形の対角線のベクトルが \( \overrightarrow{a}+\overrightarrow{b} \) である






