- 数学C|平面上のベクトル「ベクトルと平行四辺形の条件」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|ベクトルと平行四辺形の条件
平面上のベクトル 04☆四角形 \(\rm ABCD\) において、\(\overrightarrow{\rm AB}=\overrightarrow{\rm DC}\) のとき、\(\overrightarrow{\rm AD}=\overrightarrow{\rm BC}\) であることの証明方法は?
高校数学C|平面上のベクトル
解法のPoint
ベクトルと平行四辺形の条件
Point:ベクトルと平行四辺形の条件
等しいベクトル \(\overrightarrow{\rm AB}=\overrightarrow{\rm DC}\) は、
大きさが等しい \(|\,\overrightarrow{\rm AB}\,|=|\,\overrightarrow{\rm DC}\,|\)
向きが等しい=平行 \(\overrightarrow{\rm AB}\,//\,\overrightarrow{\rm DC}\)
が成り立つので、
1組の対辺が平行かつ長さが等しいので、四角形 \({\rm ABCD}\) は平行四辺形である。

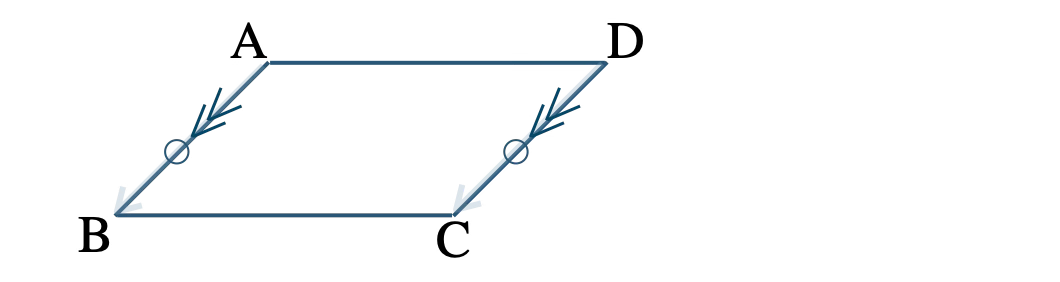
四角形 \({\rm ABCD}\) において、\(\overrightarrow{\rm AB}=\overrightarrow{\rm DC}\) のとき、
等しいベクトル \(\overrightarrow{\rm AB}=\overrightarrow{\rm DC}\) は、
大きさが等しい \(|\,\overrightarrow{\rm AB}\,|=|\,\overrightarrow{\rm DC}\,|\)
向きが等しい=平行 \(\overrightarrow{\rm AB}\,//\,\overrightarrow{\rm DC}\)
が成り立つので、
1組の対辺が平行かつ長さが等しいので、四角形 \({\rm ABCD}\) は平行四辺形である。


©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|ベクトルと平行四辺形の条件
平面上のベクトル 04☆
四角形 \(\rm ABCD\) において、\(\overrightarrow{\rm AB}=\overrightarrow{\rm DC}\) のとき、\(\overrightarrow{\rm AD}=\overrightarrow{\rm BC}\) であることの証明方法は?
高校数学C|平面上のベクトル
[証明] 四角形 \({\rm ABCD}\) において、\(\overrightarrow{\rm AB}=\overrightarrow{\rm DC}\) より、
大きさが等しいので、
\(|\,\overrightarrow{\rm AB}\,|=|\,\overrightarrow{\rm DC}\,|~ ~ ~\cdots~\small [\,1\,]\)
また、向きが等しいので平行となり、
\(\overrightarrow{\rm AB}\,//\,\overrightarrow{\rm DC}~ ~ ~\cdots~\small [\,2\,]\)
\(\small [\,1\,]\) と \(\small [\,2\,]\) より、1組の対辺が平行で長さが等しいので、四角形 \({\rm ABCD}\) は平行四辺形である
したがって、平行四辺形の対辺の性質より、
\(\overrightarrow{\rm AD}=\overrightarrow{\rm BC}\) [終]



