- 数学C|平面上のベクトル「ベクトルの実数倍の図示」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|ベクトルの実数倍の図示
高校数学C|平面上のベクトル
解法のPoint
ベクトルの実数倍の図示
ベクトル \( \overrightarrow{a} \) と実数 \( k \) において、実数倍のベクトル \( k\overrightarrow{a} \) は、
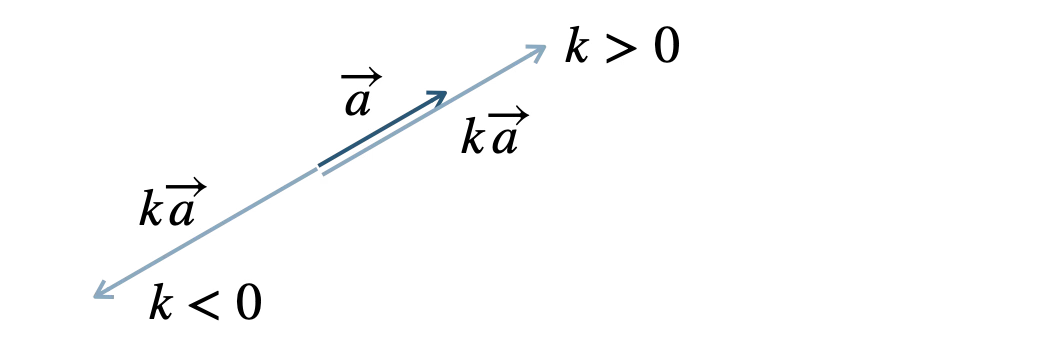

\(\overrightarrow{a} \ne \overrightarrow{0}\) のとき、
\(\small [\,1\,]\) \( k\gt 0 \) のとき、
\( \overrightarrow{a} \) と同じ向きで、大きさが \( k \) 倍
\( k=2 \) のときは、大きさが \( 2 \) 倍
\( k=1 \) のときは、等しいベクトル。
\(\small [\,2\,]\) \( k\lt 0 \) のとき、
\( \overrightarrow{a} \) と反対の向き、大きさが \( |\,k\,| \) 倍
\( k=-2 \) のときは、反対向きで大きさが \( 2 \) 倍
\( k=-1 \) のときは、逆ベクトル
\(\small [\,3\,]\) \( k=0 \) のとき、\(\begin{eqnarray}0\cdot\overrightarrow{a}&=&\overrightarrow{0}\end{eqnarray}\)
大きさが \( 0 \) となり、零ベクトルとなる。
※ \( \overrightarrow{a}=\overrightarrow{0} \) のとき、
任意の実数 \( k \) に対して、\(k\cdot \overrightarrow{a}=\overrightarrow{0}\)
零ベクトルは \( k \) 倍しても零ベクトル。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|ベクトルの実数倍の図示
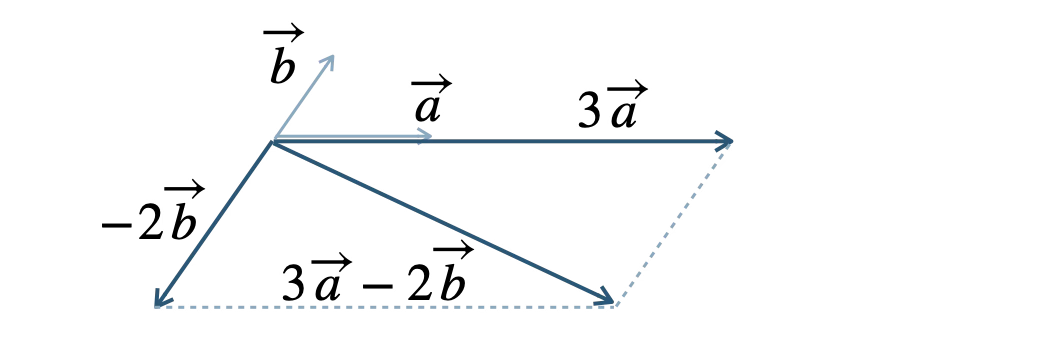
始点が同じ2つのベクトル \(\overrightarrow{a}~,~ \overrightarrow{b}\) について、\(3\overrightarrow{a}~,~ -2\overrightarrow{b}~,~ 3\overrightarrow{a}-2\overrightarrow{b}\) の図示の方法は?
高校数学C|平面上のベクトル
\( 3\overrightarrow{a} \) は、\( \overrightarrow{a} \) と同じ向きで、大きさが \( 3 \) 倍となる


\( -2\overrightarrow{b} \) は、\( \overrightarrow{b} \) と反対の向きで、大きさが \( 2 \) 倍となる


\( 3\overrightarrow{a}-2\overrightarrow{b} \) は、\( 3\overrightarrow{a} \) と \( -2\overrightarrow{b} \) の和であるので、
\( 3\overrightarrow{a} \) と \( -2\overrightarrow{b} \) を隣り合う2辺とした平行四辺形をつくり、その対角線が \( 3\overrightarrow{a}-2\overrightarrow{b} \) となる