- 数学C|平面上のベクトル「ベクトルの成分と大きさ」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|ベクトルの成分と大きさ
平面上のベクトル 13座標平面上を右に \(4\)、上に \(3\) 進む \(\overrightarrow{a}\) の成分での表し方は?また、その大きさの求め方は?
高校数学C|平面上のベクトル
解法のPoint
ベクトルの成分と大きさ
Point:ベクトルの成分と大きさ
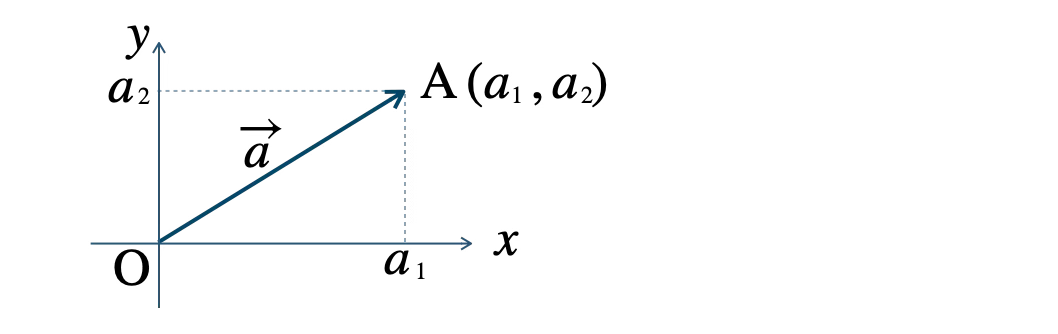
\(\overrightarrow{a}=(a_1~,~a_2)\)
となり、\(a_1\) を \(x\) 成分、\(a_2\) を \(y\) 成分という。

\(|\,\overrightarrow{a}\,|=\displaystyle \sqrt{\,{a_1}^{2}+{a_2}^{2}\,}\)
となる。
座標平面上の原点 \(\rm O\) から点 \(A(a_1~,~a_2)\) までを結んだベクトル \(\overrightarrow{\rm OA}=\overrightarrow{a}\) の成分表示は、
\(\overrightarrow{a}=(a_1~,~a_2)\)
となり、\(a_1\) を \(x\) 成分、\(a_2\) を \(y\) 成分という。


また、\(\overrightarrow{a}=(a_1~,~a_2)\) の大きさは、
\(|\,\overrightarrow{a}\,|=\displaystyle \sqrt{\,{a_1}^{2}+{a_2}^{2}\,}\)
となる。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|ベクトルの成分と大きさ
平面上のベクトル 13
座標平面上を右に \(4\)、上に \(3\) 進む \(\overrightarrow{a}\) の成分での表し方は?また、その大きさの求め方は?
高校数学C|平面上のベクトル
座標平面上を右に \(4\)、上に \(3\) 進むベクトル \(\overrightarrow{a}\) の成分表示は、
原点から進んだ場合、点 \((4~,~3)\) まで進むベクトルとなるので、
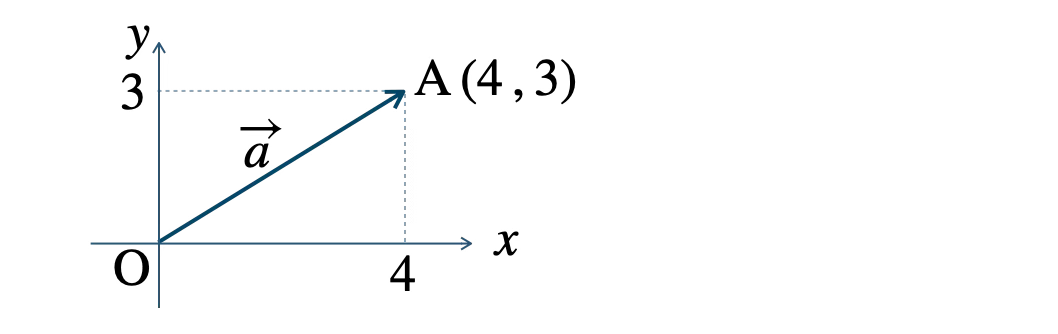

\(\overrightarrow{a}=(4~,~3)\) となる
また、\(\overrightarrow{a}=(4~,~3)\) の大きさは、
\(\begin{eqnarray}~~~|\,\overrightarrow{a}\,|&=&\displaystyle \sqrt{\,4^2+3^2\,}
\\[3pt]~~~&=&\sqrt{\,16+9\,}
\\[3pt]~~~&=&\sqrt{\,25\,}
\\[3pt]~~~&=&5
\end{eqnarray}\)



