- 数学C|平面上のベクトル「平行四辺形となるベクトルの条件」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|平行四辺形となるベクトルの条件
高校数学C|平面上のベクトル
解法のPoint
平行四辺形となるベクトルの条件
四角形 \({\rm ABCD}\) が平行四辺形となるための条件は、
\({\rm AD}={\rm BC}\) かつ \({\rm AD}\,//\,{\rm BC}\)
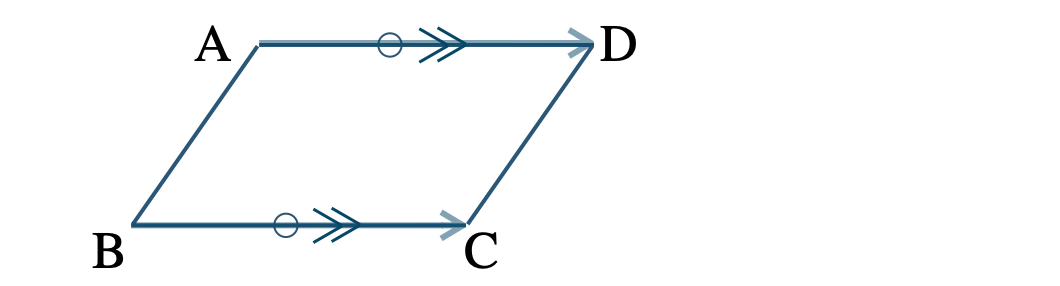


ベクトルを用いて表すと、
\(\overrightarrow{\rm AD}=\overrightarrow{\rm BC}\)
これより、\(\overrightarrow{\rm AD}~,~\overrightarrow{\rm BC}\) の成分をそれぞれ計算し、\(x\) 成分と \(y\) 成分がそれぞれ等しいことを用いて座標を求める。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|平行四辺形となるベクトルの条件
平面上の4点 \({\rm A}(4~,~ -5)~,~ {\rm B}(-2~,~ 3)~,~\)\({\rm C}(5~,~ 4)~,~\)\({\rm D}\) を頂点とする四角形が平行四辺形 \({\rm ABCD}\) となるとき、点 \({\rm D}\) の座標の求め方は?
高校数学C|平面上のベクトル
四角形 \({\rm ABCD}\) が平行四辺形となるためには、
\({\rm AD}={\rm BC}\) かつ \({\rm AD}\,//\,{\rm BC}\)



これより、
\(\overrightarrow{\rm AD}=\overrightarrow{\rm BC}\) となればよい
点 \({\rm D}\) の座標を \({\rm D}(x~,~y)\) とおき、\(\overrightarrow{\rm AD}\) と \(\overrightarrow{\rm BC}\) を成分で表すと、(原点を \({\rm O}\) として)
\(\begin{eqnarray}~~~\overrightarrow{\rm AD}&=&\overrightarrow{\rm OD}-\overrightarrow{\rm OA}
\\[5pt]~~~&=&\left(\,\begin{array}{c}x\\[2pt]y\end{array}\,\right)-\left(\,\begin{array}{c}4\\[2pt]-5\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}x-4\\[2pt]y+5\end{array}\,\right)
\end{eqnarray}\)
\(\begin{eqnarray}~~~\overrightarrow{\rm BC}&=&\overrightarrow{\rm OC}-\overrightarrow{\rm OB}
\\[5pt]~~~&=&\left(\,\begin{array}{c}5\\[2pt]4\end{array}\,\right)-\left(\,\begin{array}{c}-2\\[2pt]3\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}5+2\\[2pt]4-3\end{array}\,\right)
\\[5pt]~~~&=&\left(\,\begin{array}{c}7\\[2pt]1\end{array}\,\right)
\end{eqnarray}\)
\(\overrightarrow{\rm AD}=\overrightarrow{\rm BC}\) より、\(x\) 成分と \(y\) 成分がそれぞれ等しいので、
\(\begin{eqnarray}~~~\left\{~\begin{array}{l}
x-4=7\\[2pt]
y+5=1
\end{array}\right.
~\Leftrightarrow ~
\left\{~\begin{array}{l}
x=11\\[2pt]
y=-4
\end{array}\right.
\end{eqnarray}\)
したがって、点 \({\rm D}\) は \({\rm D}(11~,~-4)\) となる
※ 教科書などの方法の横並びだと式が長くなり、対応する成分を見落として計算ミスが増えます。ここでは成分を縦に並べて、上から順に対応する成分同士を計算できるようにしています。ただし、答えを書くときは横並びに戻しておきましょう。



