- 数学C|平面上のベクトル「三角形の射影とベクトルの内積」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|三角形の射影とベクトルの内積
平面上のベクトル 25☆\(\triangle {\rm OAB}\) の点 \({\rm A}\) から辺 \({\rm OB}\) におろした垂線と辺 \({\rm OB}\) との交点を \({\rm P}\)、点 \({\rm B}\) から辺 \({\rm OA}\) におろした垂線と辺 \({\rm OA}\) との交点を \({\rm Q}\) とするとき、\(|\overrightarrow{\rm OA}|\, |\overrightarrow{\rm OQ}|=|\overrightarrow{\rm OB}|\, |\overrightarrow{\rm OP}|\) であることの証明方法は?
高校数学C|平面上のベクトル
解法のPoint
三角形の射影とベクトルの内積
Point:三角形の射影とベクトルの内積



\(\triangle \rm OAB\) の点 \(\rm A\) から辺 \(\rm OB\) におろした垂線と辺 \(\rm OB\) の交点を \(\rm P\) とし、\(\angle \rm AOB=\theta \) とおくと、
\(\overrightarrow{\rm OA}\) と \(\overrightarrow{\rm OB}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}&=&|\,\overrightarrow{\rm OA}\,|\,|\,\overrightarrow{\rm OB}\,|cos\theta
\end{eqnarray}\)
また、\(\triangle \rm AOP\) の余弦より、
\(\begin{eqnarray}~~~\cos\theta&=&\displaystyle \frac{\,|\,\overrightarrow{\rm OP}\,|\,}{\,|\,\overrightarrow{\rm OA}\,|\,}~\Leftrightarrow ~ |\,\overrightarrow{\rm OA}\,|\cdot\cos\theta&=&|\,\overrightarrow{\rm OP}\,|
\end{eqnarray}\)
これより、
\(\begin{eqnarray}~~~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}&=&|\,\overrightarrow{\rm OB}\,|\,|\,\overrightarrow{\rm OP}\,|
\end{eqnarray}\)
この式を用いて、証明していく。
三角形の射影とベクトルの内積についての証明問題は、



\(\triangle \rm OAB\) の点 \(\rm A\) から辺 \(\rm OB\) におろした垂線と辺 \(\rm OB\) の交点を \(\rm P\) とし、\(\angle \rm AOB=\theta \) とおくと、
\(\overrightarrow{\rm OA}\) と \(\overrightarrow{\rm OB}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}&=&|\,\overrightarrow{\rm OA}\,|\,|\,\overrightarrow{\rm OB}\,|cos\theta
\end{eqnarray}\)
また、\(\triangle \rm AOP\) の余弦より、
\(\begin{eqnarray}~~~\cos\theta&=&\displaystyle \frac{\,|\,\overrightarrow{\rm OP}\,|\,}{\,|\,\overrightarrow{\rm OA}\,|\,}~\Leftrightarrow ~ |\,\overrightarrow{\rm OA}\,|\cdot\cos\theta&=&|\,\overrightarrow{\rm OP}\,|
\end{eqnarray}\)
これより、
\(\begin{eqnarray}~~~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}&=&|\,\overrightarrow{\rm OB}\,|\,|\,\overrightarrow{\rm OP}\,|
\end{eqnarray}\)
この式を用いて、証明していく。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|三角形の射影とベクトルの内積
平面上のベクトル 25☆
\(\triangle {\rm OAB}\) の点 \({\rm A}\) から辺 \({\rm OB}\) におろした垂線と辺 \({\rm OB}\) との交点を \({\rm P}\)、点 \({\rm B}\) から辺 \({\rm OA}\) におろした垂線と辺 \({\rm OA}\) との交点を \({\rm Q}\) とするとき、\(|\overrightarrow{\rm OA}|\, |\overrightarrow{\rm OQ}|=|\overrightarrow{\rm OB}|\, |\overrightarrow{\rm OP}|\) であることの証明方法は?
高校数学C|平面上のベクトル
[証明]
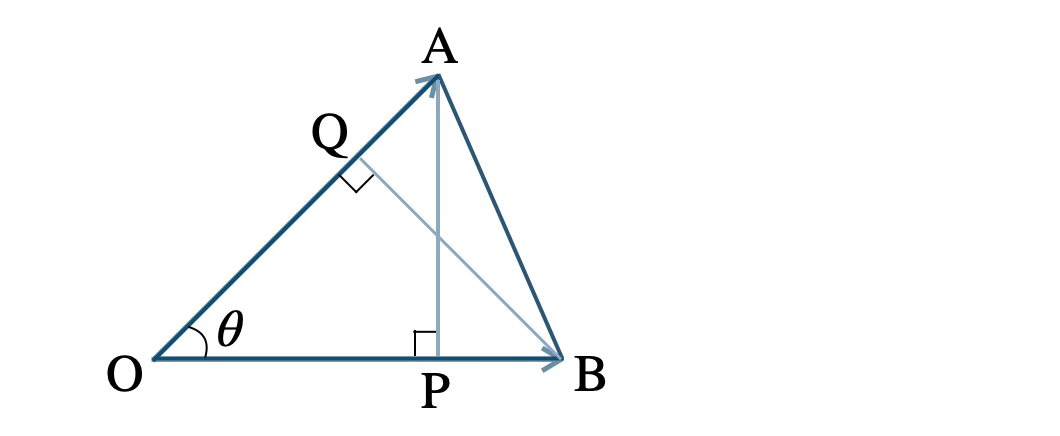
\(\angle \rm AOB=\theta \) とおくと、\(\overrightarrow{\rm OA}\) と \(\overrightarrow{\rm OB}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}&=&|\,\overrightarrow{\rm OA}\,|\,|\,\overrightarrow{\rm OB}\,|\cos \theta~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)

ここで、\(\triangle \rm AOP\) の余弦より、
\(\begin{eqnarray}~~~\cos \theta&=&\displaystyle \frac{\,|\,\overrightarrow{\rm OP}\,|\,}{\,|\,\overrightarrow{\rm OA}\,|\,}
\end{eqnarray}\)
よって、
\(\begin{eqnarray}~~~|\,\overrightarrow{\rm OA}\,|\cos \theta&=&|\,\overrightarrow{\rm OP}\,|
\end{eqnarray}\)
\(\small [\,1\,]\) に代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}&=&|\,\overrightarrow{\rm OB}\,|\cdot|\,\overrightarrow{\rm OP}\,|~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
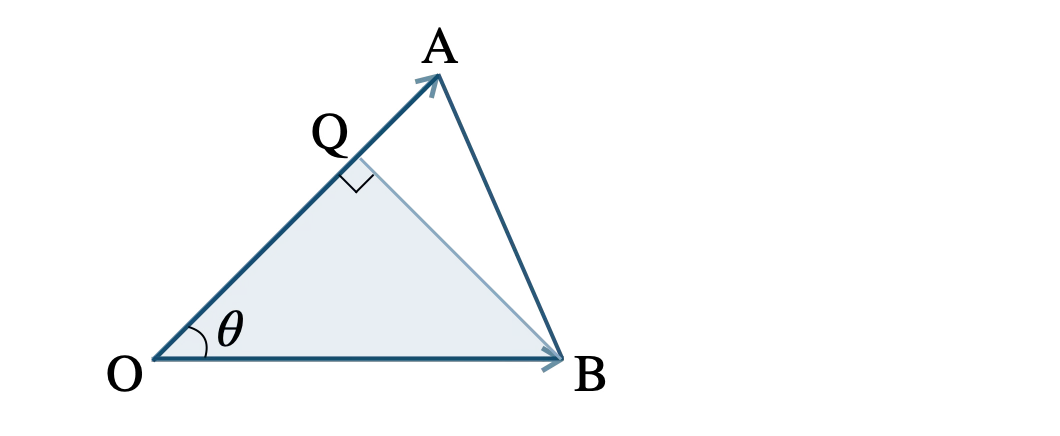
また、\(\triangle \rm OBQ\) の余弦より、
\(\begin{eqnarray}~~~\cos \theta&=&\displaystyle \frac{\,|\,\overrightarrow{\rm OQ}\,|\,}{\,|\,\overrightarrow{\rm OB}\,|\,}
\end{eqnarray}\)
よって、
\(\begin{eqnarray}~~~|\,\overrightarrow{\rm OB}\,|\cos \theta&=&|\,\overrightarrow{\rm OQ}\,|
\end{eqnarray}\)
\(\small [\,1\,]\) に代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}&=&|\,\overrightarrow{\rm OA}\,|\cdot|\,\overrightarrow{\rm OQ}\,|~ ~ ~ \cdots {\small [\,3\,]}
\end{eqnarray}\)
したがって、\(\small [\,2\,]\) と \(\small [\,3\,]\) より、
\(\begin{eqnarray}~~~|\,\overrightarrow{\rm OA}\,|\,|\,\overrightarrow{\rm OQ}\,|&=&|\,\overrightarrow{\rm OB}\,|\,|\,\overrightarrow{\rm OP}\,|
\end{eqnarray}\) [終]



