- 数学C|平面上のベクトル「角の二等分線とベクトル」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|角の二等分線とベクトル
平面上のベクトル 40☆\(\overrightarrow{a}=(2~,~-1)~,~\overrightarrow{b}=(2~,~4)\) とするとき、この2つのベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) のなす角を二等分する単位ベクトルの求め方は?
高校数学C|平面上のベクトル
解法のPoint
角の二等分線とベクトル
Point:角の二等分線とベクトル
① \(\overrightarrow{a}\) と \(\overrightarrow{b}\) の大きさを求めて、それぞれの同じ向きの単位ベクトルを求める。

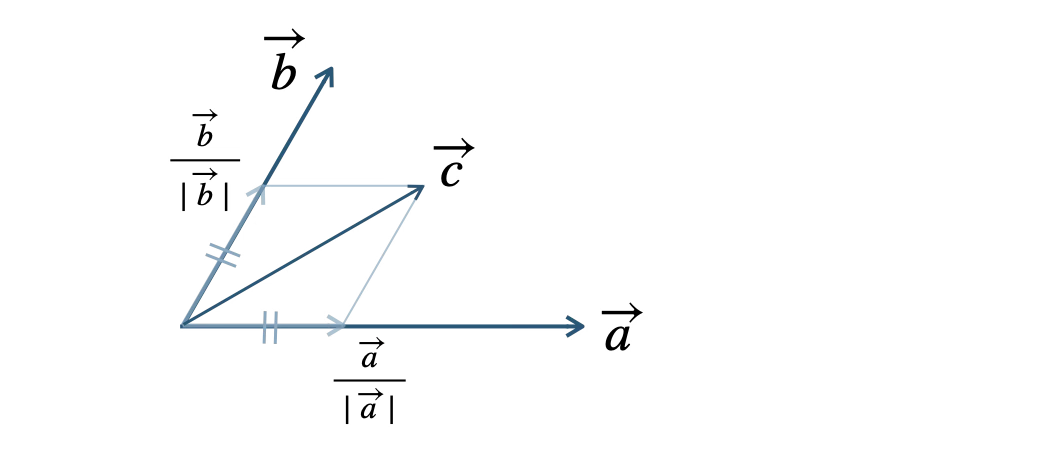
※ \(\displaystyle\frac{\,\overrightarrow{a}\,}{\,|\,\overrightarrow{a}\,|\,}\) と \(\displaystyle\frac{\,\overrightarrow{b}\,}{\,|\,\overrightarrow{b}\,|\,}\) により、ひし形をつくる。
② ひし形の対角線が二等分線となるので、角を二等分するベクトルの1つを \(\overrightarrow{c}\) として求める。
\(\overrightarrow{c}=\displaystyle\frac{\,\overrightarrow{a}\,}{\,|\,\overrightarrow{a}\,|\,}+\frac{\,\overrightarrow{b}\,}{\,|\,\overrightarrow{b}\,|\,}\)
③ \(\overrightarrow{c}\) の大きさを求めて、単位ベクトルとする。
2つのベクトル \(\overrightarrow{a}~,~\overrightarrow{b}\) のなす角を二等分するベクトルは、
① \(\overrightarrow{a}\) と \(\overrightarrow{b}\) の大きさを求めて、それぞれの同じ向きの単位ベクトルを求める。


※ \(\displaystyle\frac{\,\overrightarrow{a}\,}{\,|\,\overrightarrow{a}\,|\,}\) と \(\displaystyle\frac{\,\overrightarrow{b}\,}{\,|\,\overrightarrow{b}\,|\,}\) により、ひし形をつくる。
② ひし形の対角線が二等分線となるので、角を二等分するベクトルの1つを \(\overrightarrow{c}\) として求める。
\(\overrightarrow{c}=\displaystyle\frac{\,\overrightarrow{a}\,}{\,|\,\overrightarrow{a}\,|\,}+\frac{\,\overrightarrow{b}\,}{\,|\,\overrightarrow{b}\,|\,}\)
③ \(\overrightarrow{c}\) の大きさを求めて、単位ベクトルとする。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|角の二等分線とベクトル
平面上のベクトル 40☆
\(\overrightarrow{a}=(2~,~-1)~,~\overrightarrow{b}=(2~,~4)\) とするとき、この2つのベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) のなす角を二等分する単位ベクトルの求め方は?
高校数学C|平面上のベクトル
\(\overrightarrow{a}=\begin{pmatrix}2\\-1\end{pmatrix}~,~\overrightarrow{b}=\begin{pmatrix}2\\4\end{pmatrix}\) のとき、
\(\begin{eqnarray}~~~|\,\overrightarrow{a}\,|&=&\sqrt{2^2+(-1)^2}
\\[3pt]~~~&=&\sqrt{4+1}
\\[3pt]~~~&=&\sqrt{5}\end{eqnarray}\)
\(\begin{eqnarray}~~~|\,\overrightarrow{b}\,|&=&\sqrt{2^2+4^2}
\\[3pt]~~~&=&\sqrt{4+16}
\\[3pt]~~~&=&\sqrt{20}
\\[3pt]~~~&=&2\sqrt{5}\end{eqnarray}\)
\(\overrightarrow{a}\) と \(\overrightarrow{b}\) のなす角を二等分するベクトルの1つを \(\overrightarrow{c}\) とすると、
\(\overrightarrow{c}=\displaystyle\frac{\,\overrightarrow{a}\,}{\,|\,\overrightarrow{a}\,|\,}+\frac{\,\overrightarrow{b}\,}{\,|\,\overrightarrow{b}\,|\,}\) となるので、
\(\begin{eqnarray}~~~\overrightarrow{c}&=&\displaystyle\frac{\,1\,}{\,\sqrt{5}\,}\begin{pmatrix}2\\-1\end{pmatrix}+\frac{\,1\,}{\,2\sqrt{5}\,}\begin{pmatrix}2\\4\end{pmatrix}
\\[5pt]~~~&=&\begin{pmatrix}\displaystyle\frac{\,2\,}{\,\sqrt{5}\,}+\frac{\,1\,}{\,\sqrt{5}\,}\\[3pt]\displaystyle\frac{\,-1\,}{\,\sqrt{5}\,}+\frac{\,2\,}{\,\sqrt{5}\,}\end{pmatrix}
\\[5pt]~~~&=&\left(\displaystyle\frac{\,3\,}{\,\sqrt{5}\,}~,~\frac{\,1\,}{\,\sqrt{5}\,}\right)\end{eqnarray}\)
ここで、\(\overrightarrow{c}\) の大きさは、
\(\begin{eqnarray}~~~|\,\overrightarrow{c}\,|&=&\sqrt{\left(\displaystyle\frac{\,3\,}{\,\sqrt{5}\,}\right)^2+\left(\displaystyle\frac{\,1\,}{\,\sqrt{5}\,}\right)^2}
\\[5pt]~~~&=&\sqrt{\displaystyle\frac{\,9\,}{\,5\,}+\frac{\,1\,}{\,5\,}}
\\[5pt]~~~&=&\sqrt{\displaystyle\frac{\,10\,}{\,5\,}}
\\[5pt]~~~&=&\sqrt{2}\end{eqnarray}\)
よって、単位ベクトルは \(\displaystyle\frac{\,\overrightarrow{c}\,}{\,|\,\overrightarrow{c}\,|\,}\) と \(-\displaystyle\frac{\,\overrightarrow{c}\,}{\,|\,\overrightarrow{c}\,|\,}\) の2つあるので、
\(\begin{eqnarray}~~~\displaystyle\frac{\,\overrightarrow{c}\,}{\,|\,\overrightarrow{c}\,|\,}&=&\frac{\,1\,}{\,\sqrt{2}\,}\left(\frac{\,3\,}{\,\sqrt{5}\,}~,~\frac{\,1\,}{\,\sqrt{5}\,}\right)
\\[5pt]~~~&=&\left(\frac{\,3\,}{\,\sqrt{10}\,}~,~\frac{\,1\,}{\,\sqrt{10}\,}\right)
\end{eqnarray}\)
\(\begin{eqnarray}~~~-\displaystyle\frac{\,\overrightarrow{c}\,}{\,|\,\overrightarrow{c}\,|\,}&=&-\frac{\,1\,}{\,\sqrt{2}\,}\cdot\left(\frac{\,3\,}{\,\sqrt{5}\,}~,~\frac{\,1\,}{\,\sqrt{5}\,}\right)
\\[5pt]~~~&=&\left(-\frac{\,3\,}{\,\sqrt{10}\,}~,~-\frac{\,1\,}{\,\sqrt{10}\,}\right)
\end{eqnarray}\)
したがって、求める単位ベクトル \(\overrightarrow{e}\) は、
\(\overrightarrow{e}=\left(\displaystyle\frac{\,3\,}{\,\sqrt{10}\,}~,~\frac{\,1\,}{\,\sqrt{10}\,}\right)\)
\(\overrightarrow{e}=\left(-\displaystyle\frac{\,3\,}{\,\sqrt{10}\,}~,~-\frac{\,1\,}{\,\sqrt{10}\,}\right)\)



