このページは、「角の二等分線とベクトル」の練習問題アーカイブページとなります。
この問題の解き方の詳細は↓
角の二等分線とベクトル で確認できます。
問題アーカイブ01
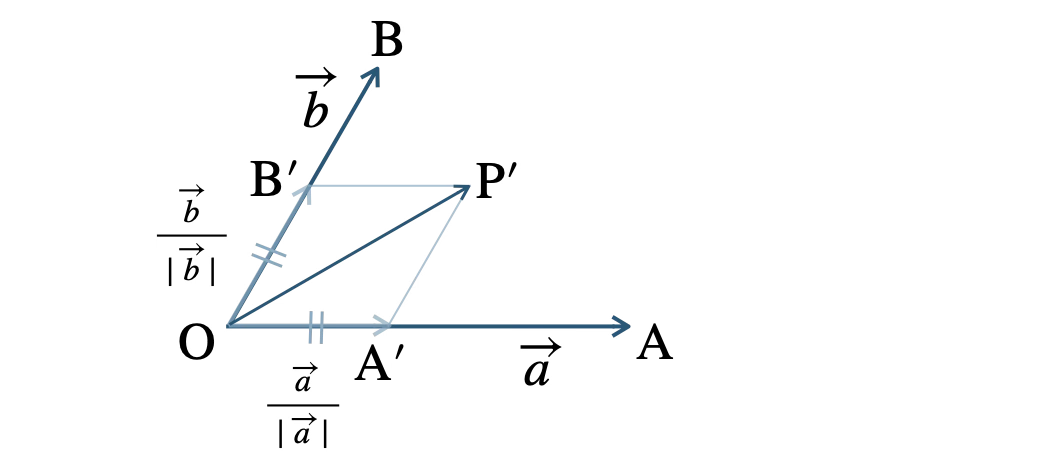
問題アーカイブ01平面上の異なる3点 \({\rm O}~,~{\rm A}~,~{\rm B}\) が一直線上に並んでいないとし、\(\overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}\) とおく。\(\overrightarrow{p}=t\left(\displaystyle\frac{\,\overrightarrow{a}\,}{\,|\,\overrightarrow{a}\,|\,}+\frac{\,\overrightarrow{b}\,}{\,|\,\overrightarrow{b}\,|\,}\right)\) で表される点 \({\rm P}(\overrightarrow{p})\) は、\(\angle {\rm AOB}\) の二等分線上にあることを証明せよ。
東京書籍|Advanced数学C[701] p.69 練習問題B 9
[証明]
\(\overrightarrow{\rm OA’}=\displaystyle\frac{\,\overrightarrow{a}\,}{\,|\,\overrightarrow{a}\,|\,}~,~\overrightarrow{\rm OB’}=\displaystyle\frac{\,\overrightarrow{b}\,}{\,|\,\overrightarrow{b}\,|\,}\) となる点 \({\rm A’}~,~{\rm B’}\) をとると、
\(|\,\overrightarrow{\rm OA’}\,|=|\,\overrightarrow{\rm OB’}\,|=1\)
さらに、\(\overrightarrow{\rm OA’}+\overrightarrow{\rm OB’}=\overrightarrow{\rm OP’}\) となる点 \({\rm P’}\) をとると、
\(\overrightarrow{\rm A’P’}=\overrightarrow{\rm OB’}~,~\overrightarrow{\rm B’P’}=\overrightarrow{\rm OA’}\)
となるので、四角形 \({\rm OA’P’B’}\) は平行四辺形である。
また、\(|\,\overrightarrow{\rm OA’}\,|=|\,\overrightarrow{\rm OB’}\,|=1\) より、
\({\rm OA’}={\rm OB’}={\rm A’P’}={\rm B’P’}=1\)
となるので、四角形 \({\rm OA’P’B’}\) はひし形である。
ひし形の対角線は角を二等分するので、\({\rm OP’}\) は \(\angle {\rm A’OB’}\) を二等分する。
ここで、\(\angle {\rm A’OB’}=\angle {\rm AOB}\) であるから、\({\rm OP’}\) は \(\angle {\rm AOB}\) の二等分線上にある。
\(\overrightarrow{\rm OP’}=\displaystyle\frac{\,\overrightarrow{a}\,}{\,|\,\overrightarrow{a}\,|\,}+\frac{\,\overrightarrow{b}\,}{\,|\,\overrightarrow{b}\,|\,}\) の方向が二等分線の方向となるので、
\(\overrightarrow{p}=t\left(\displaystyle\frac{\,\overrightarrow{a}\,}{\,|\,\overrightarrow{a}\,|\,}+\frac{\,\overrightarrow{b}\,}{\,|\,\overrightarrow{b}\,|\,}\right)\) で表される点 \({\rm P}(\overrightarrow{p})\) は \(\angle {\rm AOB}\) の二等分線上にある。[終]
問題アーカイブ02
問題アーカイブ02\(\overrightarrow{\rm OA}=(4~,~2)~,~\overrightarrow{\rm OB}=(-1~,~-2)\) とするとき、始点を \({\rm O}\) とし、\(\angle {\rm AOB}\) の二等分線と平行で、大きさが \(2\) であるベクトルを求めよ。
東京書籍|Standard数学C[702] p.68 Level Up 1
\(\overrightarrow{\rm OA}=\begin{pmatrix}4\\2\end{pmatrix}~,~\overrightarrow{\rm OB}=\begin{pmatrix}-1\\-2\end{pmatrix}\) のとき、
\(\begin{eqnarray}~~~|\,\overrightarrow{\rm OA}\,|&=&\sqrt{4^2+2^2}
\\[3pt]~~~&=&\sqrt{16+4}
\\[3pt]~~~&=&\sqrt{20}
\\[3pt]~~~&=&2\sqrt{5}\end{eqnarray}\)
\(\begin{eqnarray}~~~|\,\overrightarrow{\rm OB}\,|&=&\sqrt{(-1)^2+(-2)^2}
\\[3pt]~~~&=&\sqrt{1+4}
\\[3pt]~~~&=&\sqrt{5}\end{eqnarray}\)
\(\overrightarrow{\rm OA}\) と \(\overrightarrow{\rm OB}\) のなす角を二等分するベクトルの1つを \(\overrightarrow{c}\) とすると、
\(\overrightarrow{c}=\displaystyle\frac{\,\overrightarrow{\rm OA}\,}{\,|\,\overrightarrow{\rm OA}\,|\,}+\frac{\,\overrightarrow{\rm OB}\,}{\,|\,\overrightarrow{\rm OB}\,|\,}\) となるので、
\(\begin{eqnarray}~~~\overrightarrow{c}&=&\displaystyle\frac{\,1\,}{\,2\sqrt{5}\,}\begin{pmatrix}4\\2\end{pmatrix}+\frac{\,1\,}{\,\sqrt{5}\,}\begin{pmatrix}-1\\-2\end{pmatrix}
\\[5pt]~~~&=&\begin{pmatrix}\displaystyle\frac{\,2\,}{\,\sqrt{5}\,}+\frac{\,-1\,}{\,\sqrt{5}\,}\\[3pt]\displaystyle\frac{\,1\,}{\,\sqrt{5}\,}+\frac{\,-2\,}{\,\sqrt{5}\,}\end{pmatrix}
\\[5pt]~~~&=&\left(\displaystyle\frac{\,1\,}{\,\sqrt{5}\,}~,~-\frac{\,1\,}{\,\sqrt{5}\,}\right)\end{eqnarray}\)
ここで、\(\overrightarrow{c}\) の大きさは、
\(\begin{eqnarray}~~~|\,\overrightarrow{c}\,|&=&\sqrt{\left(\displaystyle\frac{\,1\,}{\,\sqrt{5}\,}\right)^2+\left(-\displaystyle\frac{\,1\,}{\,\sqrt{5}\,}\right)^2}
\\[5pt]~~~&=&\sqrt{\displaystyle\frac{\,1\,}{\,5\,}+\frac{\,1\,}{\,5\,}}
\\[5pt]~~~&=&\sqrt{\displaystyle\frac{\,2\,}{\,5\,}}\end{eqnarray}\)
よって、大きさが \(2\) のベクトルは \(2\cdot\displaystyle\frac{\,\overrightarrow{c}\,}{\,|\,\overrightarrow{c}\,|\,}\) と \(-2\cdot\displaystyle\frac{\,\overrightarrow{c}\,}{\,|\,\overrightarrow{c}\,|\,}\) の2つあるので、
\(\begin{eqnarray}~~~2\cdot\displaystyle\frac{\,\overrightarrow{c}\,}{\,|\,\overrightarrow{c}\,|\,}&=&\frac{\,2\,}{\,\sqrt{\displaystyle \frac{\,2\,}{\,5\,}}\,}\left(\frac{\,1\,}{\,\sqrt{5}\,}~,~-\frac{\,1\,}{\,\sqrt{5}\,}\right)
\\[5pt]~~~&=&\sqrt{10}\left(\frac{\,1\,}{\,\sqrt{5}\,}~,~-\frac{\,1\,}{\,\sqrt{5}\,}\right)
\\[5pt]~~~&=&\left(\sqrt{2}~,~-\sqrt{2}\right)
\end{eqnarray}\)
\(\begin{eqnarray}~~~-2\cdot\displaystyle\frac{\,\overrightarrow{c}\,}{\,|\,\overrightarrow{c}\,|\,}&=&-\sqrt{10}\cdot\left(\frac{\,1\,}{\,\sqrt{5}\,}~,~-\frac{\,1\,}{\,\sqrt{5}\,}\right)
\\[5pt]~~~&=&\left(-\sqrt{2}~,~\sqrt{2}\right)
\end{eqnarray}\)
したがって、求める大きさが \(2\) のベクトル \(\overrightarrow{e}\) は、
\(\overrightarrow{e}=\left(\sqrt{2}~,~-\sqrt{2}\right)\)
\(\overrightarrow{e}=\left(-\sqrt{2}~,~\sqrt{2}\right)\)