- 数学C|平面上のベクトル「位置ベクトルと2点を結ぶベクトル」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|位置ベクトルと2点を結ぶベクトル
平面上のベクトル 43\({\rm A}(\overrightarrow{a})~,~ {\rm B}(\overrightarrow{b})\) のとき、\(\overrightarrow{\rm AB}\) や \(\overrightarrow{\rm BA}\) を \(\overrightarrow{a}~,~ \overrightarrow{b}\) を用いて表す方法は?
高校数学C|平面上のベクトル
解法のPoint
位置ベクトルと2点を結ぶベクトル
Point:位置ベクトルと2点を結ぶベクトル
点 \(\rm A\)の位置は、ベクトル \(\overrightarrow{\rm OA}=\overrightarrow{a}\) で表され、
この \(\overrightarrow{a}\) を \(\rm A\) の「位置ベクトル」といい、点 \(\rm A\) を \( {\rm A}(\overrightarrow{a}) \) と表す。

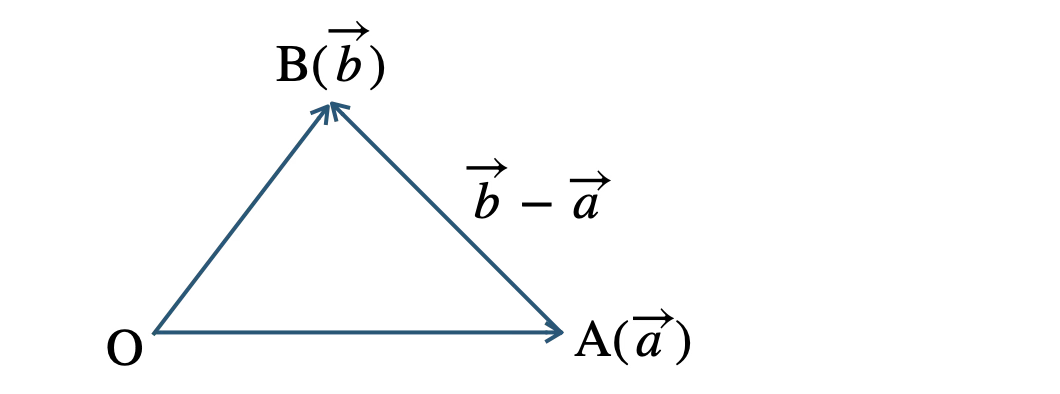
\(\begin{eqnarray}\overrightarrow{\rm AB}&=&\overrightarrow{b}-\overrightarrow{a}
\end{eqnarray}\)
1点 \(\rm O\) を固定したとき、
点 \(\rm A\)の位置は、ベクトル \(\overrightarrow{\rm OA}=\overrightarrow{a}\) で表され、
この \(\overrightarrow{a}\) を \(\rm A\) の「位置ベクトル」といい、点 \(\rm A\) を \( {\rm A}(\overrightarrow{a}) \) と表す。
また、2点 \( {\rm A}(\overrightarrow{a})~,~{\rm B}(\overrightarrow{b}) \) に対して、


\(\begin{eqnarray}\overrightarrow{\rm AB}&=&\overrightarrow{b}-\overrightarrow{a}
\end{eqnarray}\)
※ 矢印の先の点 \({\rm B}\) から先に書く。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|位置ベクトルと2点を結ぶベクトル
平面上のベクトル 43
\({\rm A}(\overrightarrow{a})~,~ {\rm B}(\overrightarrow{b})\) のとき、\(\overrightarrow{\rm AB}\) や \(\overrightarrow{\rm BA}\) を \(\overrightarrow{a}~,~ \overrightarrow{b}\) を用いて表す方法は?
高校数学C|平面上のベクトル
位置ベクトル \( {\rm A}(\overrightarrow{a})~,~{\rm B}(\overrightarrow{b}) \) において、


\(\begin{eqnarray}~~~\overrightarrow{\rm AB}&=&\overrightarrow{b}-\overrightarrow{a}\end{eqnarray}\)
※ 矢印の先の点 \({\rm B}\) が先。


\(\begin{eqnarray}~~~\overrightarrow{\rm BA}&=&\overrightarrow{a}-\overrightarrow{b}\end{eqnarray}\)
※ 矢印の先の点 \({\rm A}\) が先。



