- 数学C|平面上のベクトル「三角形と2点を結ぶ位置ベクトル」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|三角形と2点を結ぶ位置ベクトル
平面上のベクトル 45☆\(\triangle {\rm ABC}\) の辺 \({\rm BC}\) の中点を \({\rm D}\)、辺 \({\rm AD}\) を \(2:3\) に内分する点を \({\rm E}\) とするとき、\(\overrightarrow{\rm AD}~,~\overrightarrow{\rm AE}~,~\overrightarrow{\rm BE}~,~\overrightarrow{\rm EC}\) を \(\overrightarrow{\rm AB}\) と \(\overrightarrow{\rm AC}\) を用いて表す方法は?
高校数学C|平面上のベクトル
解法のPoint
三角形と2点を結ぶ位置ベクトル
Point:三角形と2点を結ぶ位置ベクトル

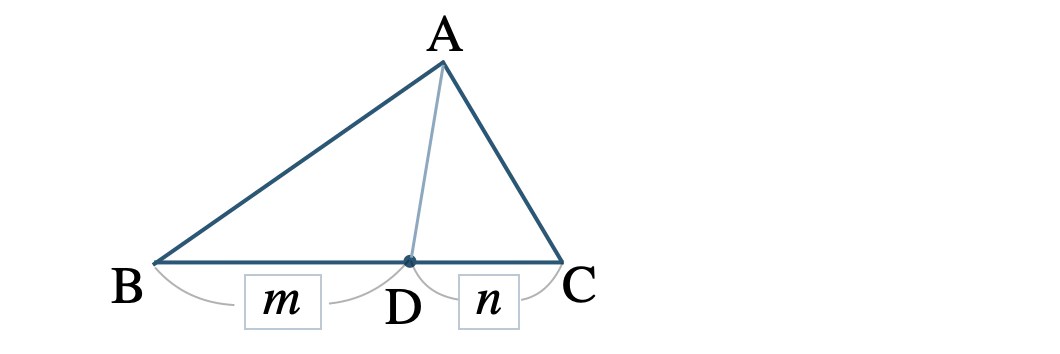
□ 内分点・外分点・中点
辺 \( {\rm BC} \) を \( m:n \) に内分する点を \( {\rm D} \) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AD}&=&\displaystyle \frac{\,n\,\overrightarrow{\rm AB}+m\,\overrightarrow{\rm AC}\,}{\,m+n\,}\end{eqnarray}\)
\( \overrightarrow{\rm BD} \) は \( \overrightarrow{\rm BC} \) の \( \displaystyle \frac{\,m\,}{\,m+n\,} \) 倍より、
\(\begin{eqnarray}~~~\overrightarrow{\rm BD}&=&\displaystyle \frac{\,m\,}{\,m+n\,}\,\overrightarrow{\rm BC}
\end{eqnarray}\)
\( \overrightarrow{\rm BC} \) の始点を \({\rm A}\) にすると、
\(\begin{eqnarray}~~~\overrightarrow{\rm BC}&=&\overrightarrow{\rm AC}-\overrightarrow{\rm AB}\end{eqnarray}\)
\( \triangle {\rm ABC} \) と2点を結ぶ位置ベクトルは、


□ 内分点・外分点・中点
辺 \( {\rm BC} \) を \( m:n \) に内分する点を \( {\rm D} \) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AD}&=&\displaystyle \frac{\,n\,\overrightarrow{\rm AB}+m\,\overrightarrow{\rm AC}\,}{\,m+n\,}\end{eqnarray}\)
□ ベクトルの実数倍
\( \overrightarrow{\rm BD} \) は \( \overrightarrow{\rm BC} \) の \( \displaystyle \frac{\,m\,}{\,m+n\,} \) 倍より、
\(\begin{eqnarray}~~~\overrightarrow{\rm BD}&=&\displaystyle \frac{\,m\,}{\,m+n\,}\,\overrightarrow{\rm BC}
\end{eqnarray}\)
□ 始点の変更
\( \overrightarrow{\rm BC} \) の始点を \({\rm A}\) にすると、
\(\begin{eqnarray}~~~\overrightarrow{\rm BC}&=&\overrightarrow{\rm AC}-\overrightarrow{\rm AB}\end{eqnarray}\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|三角形と2点を結ぶ位置ベクトル
平面上のベクトル 45☆
\(\triangle {\rm ABC}\) の辺 \({\rm BC}\) の中点を \({\rm D}\)、辺 \({\rm AD}\) を \(2:3\) に内分する点を \({\rm E}\) とするとき、\(\overrightarrow{\rm AD}~,~\overrightarrow{\rm AE}~,~\overrightarrow{\rm BE}~,~\overrightarrow{\rm EC}\) を \(\overrightarrow{\rm AB}\) と \(\overrightarrow{\rm AC}\) を用いて表す方法は?
高校数学C|平面上のベクトル
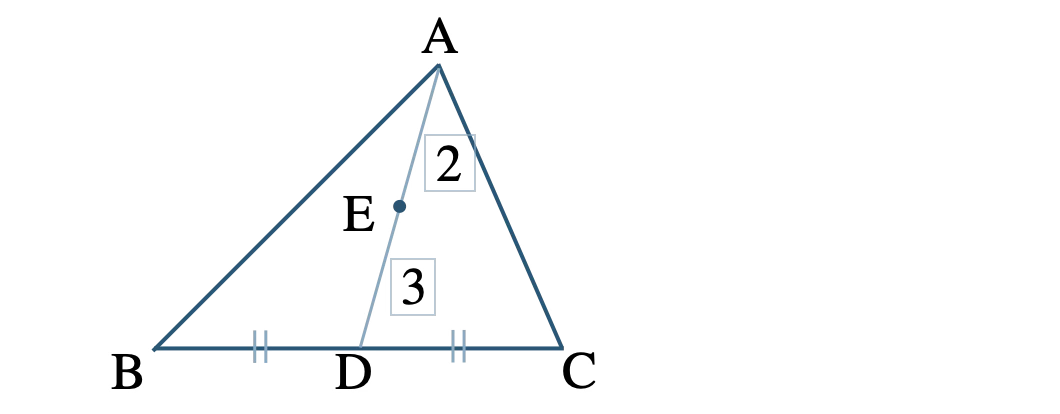
点 \( {\rm D} \) は \( {\rm BC} \) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AD}&=&\frac{\,\overrightarrow{\rm AB}+\overrightarrow{\rm AC}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm AB}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm AC}
\end{eqnarray}\)
次に、\( {\rm AE:ED}=2:3 \) より \( {\rm AE:AD}=2:5 \) となり、
\(\begin{eqnarray}~~~\overrightarrow{\rm AE}&=&\displaystyle \frac{\,2\,}{\,5\,}\overrightarrow{\rm AD}
\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,5\,}\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm AB}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm AC}\right)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{\rm AB}+\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{\rm AC}
\end{eqnarray}\)
\( \overrightarrow{\rm BE} \) の始点を \({\rm A}\) にすると、
\(\begin{eqnarray}~~~\overrightarrow{\rm BE}&=&\overrightarrow{\rm AE}-\overrightarrow{\rm AB}
\\[5pt]~~~&=&\left(\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{\rm AB}+\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{\rm AC}\right)-\overrightarrow{\rm AB}
\\[5pt]~~~&=&-\displaystyle \frac{\,4\,}{\,5\,}\overrightarrow{\rm AB}+\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{\rm AC}
\end{eqnarray}\)
同様に、\( \overrightarrow{\rm EC} \) の始点を \({\rm A}\) にすると、
\(\begin{eqnarray}~~~\overrightarrow{\rm EC}&=&\overrightarrow{\rm AC}-\overrightarrow{\rm AE}
\\[5pt]~~~&=&\overrightarrow{\rm AC}-\left(\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{\rm AB}+\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{\rm AC}\right)
\\[5pt]~~~&=&-\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{\rm AB}+\displaystyle \frac{\,4\,}{\,5\,}\overrightarrow{\rm AC}
\end{eqnarray}\)



