- 数学C|平面上のベクトル「ベクトルの内分点と等式の証明」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|ベクトルの内分点と等式の証明
平面上のベクトル 48\(\triangle {\rm ABC}\) の辺 \({\rm BC~,~ CA~,~ AB}\) をそれぞれ \(2:1\) に内分する点を \({\rm P~,~ Q~,~R}\) とするとき、\(\overrightarrow{\rm AP}+\overrightarrow{\rm BQ}+\overrightarrow{\rm CR}=\overrightarrow{0}\) であることの証明方法は?
高校数学C|平面上のベクトル
解法のPoint
ベクトルの内分点と等式の証明
Point:ベクトルの内分点と等式の証明
① 各頂点や内分点を位置ベクトルでおく。
\({\rm A}(\overrightarrow{a})~,~{\rm B}(\overrightarrow{b})~,~{\rm C}(\overrightarrow{c})\)
\({\rm P}(\overrightarrow{p})~,~{\rm Q}(\overrightarrow{q})~,~{\rm R}(\overrightarrow{r})\)
② 内分点を頂点の位置ベクトルの式で表す。
\(\begin{eqnarray}~~~\overrightarrow{p}&=&\displaystyle \frac{\,\overrightarrow{b}+2\overrightarrow{c}\,}{\,3\,}
\\[5pt]~~~\overrightarrow{q}&=&\displaystyle \frac{\,\overrightarrow{c}+2\overrightarrow{a}\,}{\,3\,}
\\[5pt]~~~\overrightarrow{r}&=&\displaystyle \frac{\,\overrightarrow{a}+2\overrightarrow{b}\,}{\,3\,}
\end{eqnarray}\)
③ 等式の左辺を位置ベクトルで表し、②を代入して等式が成り立つことを示す。
\(\triangle {\rm ABC}\) と各辺の内分点についてのベクトルの等式の証明の手順は、
① 各頂点や内分点を位置ベクトルでおく。
\({\rm A}(\overrightarrow{a})~,~{\rm B}(\overrightarrow{b})~,~{\rm C}(\overrightarrow{c})\)
\({\rm P}(\overrightarrow{p})~,~{\rm Q}(\overrightarrow{q})~,~{\rm R}(\overrightarrow{r})\)
② 内分点を頂点の位置ベクトルの式で表す。
\(\begin{eqnarray}~~~\overrightarrow{p}&=&\displaystyle \frac{\,\overrightarrow{b}+2\overrightarrow{c}\,}{\,3\,}
\\[5pt]~~~\overrightarrow{q}&=&\displaystyle \frac{\,\overrightarrow{c}+2\overrightarrow{a}\,}{\,3\,}
\\[5pt]~~~\overrightarrow{r}&=&\displaystyle \frac{\,\overrightarrow{a}+2\overrightarrow{b}\,}{\,3\,}
\end{eqnarray}\)
③ 等式の左辺を位置ベクトルで表し、②を代入して等式が成り立つことを示す。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|ベクトルの内分点と等式の証明
平面上のベクトル 48
\(\triangle {\rm ABC}\) の辺 \({\rm BC~,~ CA~,~ AB}\) をそれぞれ \(2:1\) に内分する点を \({\rm P~,~ Q~,~R}\) とするとき、\(\overrightarrow{\rm AP}+\overrightarrow{\rm BQ}+\overrightarrow{\rm CR}=\overrightarrow{0}\) であることの証明方法は?
高校数学C|平面上のベクトル
[証明]
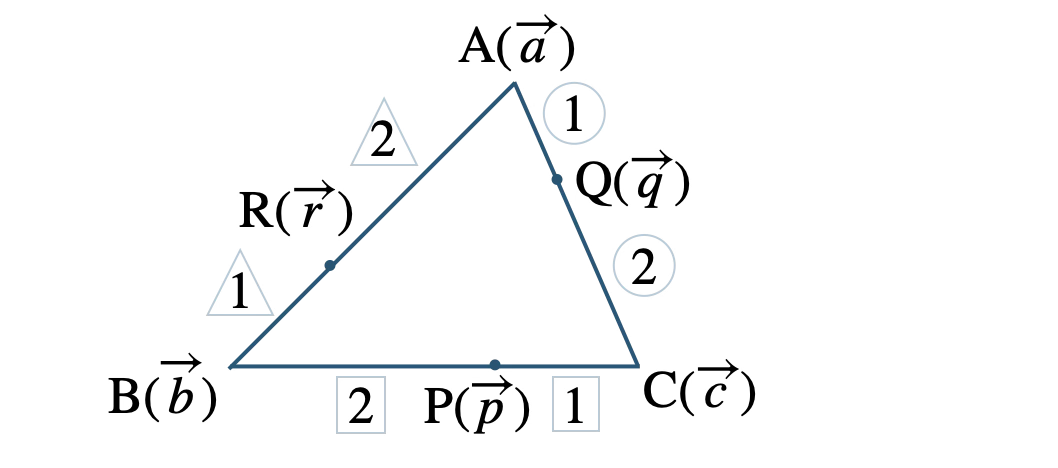
それぞれの位置ベクトルを、
\({\rm A}(\overrightarrow{a})~,~{\rm B}(\overrightarrow{b})~,~{\rm C}(\overrightarrow{c})\)
\({\rm P}(\overrightarrow{p})~,~{\rm Q}(\overrightarrow{q})~,~{\rm R}(\overrightarrow{r})\)
とおくと、
点 \({\rm P~,~ Q~,~R}\) が辺 \({\rm BC~,~ CA~,~ AB}\) をそれぞれ \(2:1\) に内分する点であることより、
\(\begin{eqnarray}~~~\overrightarrow{p}&=&\displaystyle \frac{\,1{\, \small \times \,}\overrightarrow{b}+2{\, \small \times \,}\overrightarrow{c}\,}{\,2+1\,}=\displaystyle \frac{\,\overrightarrow{b}+2\overrightarrow{c}\,}{\,3\,}
\\[5pt]~~~\overrightarrow{q}&=&\displaystyle \frac{\,1{\, \small \times \,}\overrightarrow{c}+2{\, \small \times \,}\overrightarrow{a}\,}{\,2+1\,}=\displaystyle \frac{\,\overrightarrow{c}+2\overrightarrow{a}\,}{\,3\,}
\\[5pt]~~~\overrightarrow{r}&=&\displaystyle \frac{\,1{\, \small \times \,}\overrightarrow{a}+2{\, \small \times \,}\overrightarrow{b}\,}{\,2+1\,}=\displaystyle \frac{\,\overrightarrow{a}+2\overrightarrow{b}\,}{\,3\,}
\end{eqnarray}\)
ここで、\(\overrightarrow{p}+\overrightarrow{q}+\overrightarrow{r}\) を \(\overrightarrow{a}~,~\overrightarrow{b}~,~\overrightarrow{c}\) を用いて表すと、
\(\begin{eqnarray}~~~&&\overrightarrow{p}+\overrightarrow{q}+\overrightarrow{r}
\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{b}+2\overrightarrow{c}+\overrightarrow{c}+2\overrightarrow{a}+\overrightarrow{a}+2\overrightarrow{b}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,3\overrightarrow{a}+3\overrightarrow{b}+3\overrightarrow{c}\,}{\,3\,}
\\[5pt]~~~&=&\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}
\end{eqnarray}\)
これより、等式の左辺は、
\(\begin{eqnarray}~~~&&\overrightarrow{\rm AP}+\overrightarrow{\rm BQ}+\overrightarrow{\rm CR}
\\[5pt]~~~&=&(\overrightarrow{p}-\overrightarrow{a})+(\overrightarrow{q}-\overrightarrow{b})+(\overrightarrow{r}-\overrightarrow{c})
\\[5pt]~~~&=&(\overrightarrow{p}+\overrightarrow{q}+\overrightarrow{r})-(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})-(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\overrightarrow{0}
\end{eqnarray}\)
したがって、\(\overrightarrow{\rm AP}+\overrightarrow{\rm BQ}+\overrightarrow{\rm CR}=\overrightarrow{0}\) [終]



