- 数学C|平面上のベクトル「垂直に交わることの証明(三角形の垂心)」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|垂直に交わることの証明(三角形の垂心)
平面上のベクトル 51\(\triangle {\rm ABC}\) の頂点 \(\rm B~,~ C\) から対辺に下ろした垂線の交点を \(\rm H\) とするとき、\(\rm AH \perp BC\) であることの証明方法は?
高校数学C|平面上のベクトル
解法のPoint
垂直に交わることの証明(三角形の垂心)
Point:垂直に交わることの証明(三角形の垂心)


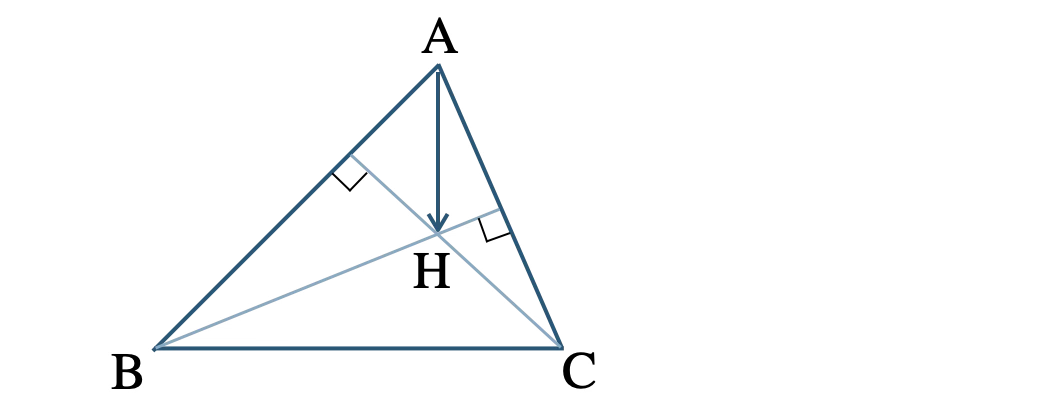
\({\rm AH \perp BC}~\Leftrightarrow ~ \overrightarrow{\rm AH}\cdot\overrightarrow{\rm BC}=0\) が目標
よって、\(\overrightarrow{\rm AH}\) と \(\overrightarrow{\rm BC}\) の内積を求める。
① 2つの基本ベクトルと 点 \({\rm H}\) を位置ベクトルでおく。
\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}~,~\overrightarrow{\rm AH}=\overrightarrow{h}\)
② 垂線の条件より、内積が \(0\) の条件式を立てる。
\(\overrightarrow{\rm BH}\perp\overrightarrow{\rm AC}\) より、\(\overrightarrow{\rm BH}\cdot\overrightarrow{\rm AC}=0\)
\(\overrightarrow{\rm CH}\perp\overrightarrow{\rm AB}\) より、\(\overrightarrow{\rm CH}\cdot\overrightarrow{\rm AB}=0\)
③ 内積 \(\overrightarrow{\rm AH}\cdot\overrightarrow{\rm BC}\) を計算して、\(0\) となることを示す。
\(\overrightarrow{\rm AH}\cdot\overrightarrow{\rm BC}=0\) より、\(\rm AH \perp BC\)
\(\triangle {\rm ABC}\) の頂点 \(\rm B~,~ C\) から対辺に下ろした垂線の交点を \(\rm H\) とするとき、\(\rm AH \perp BC\) の証明の手順は、
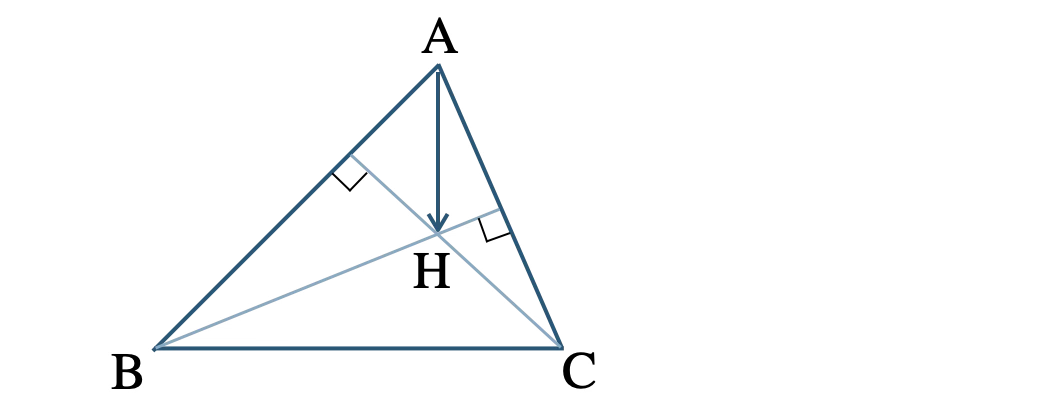
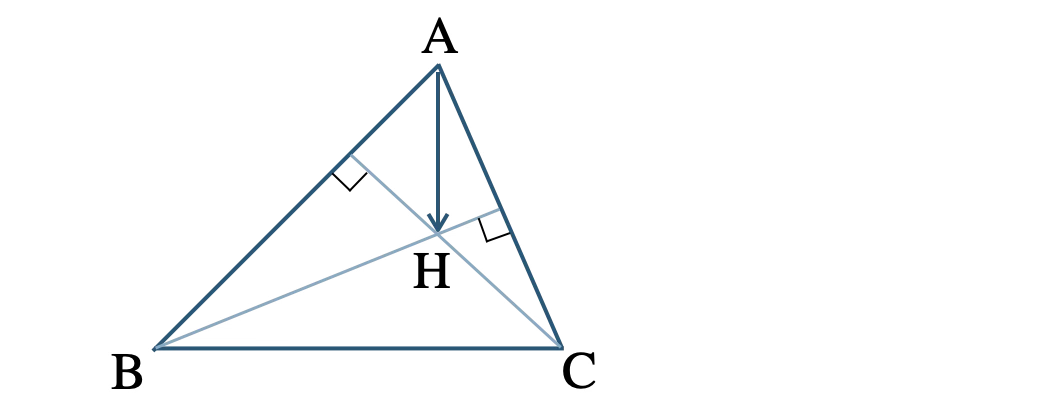
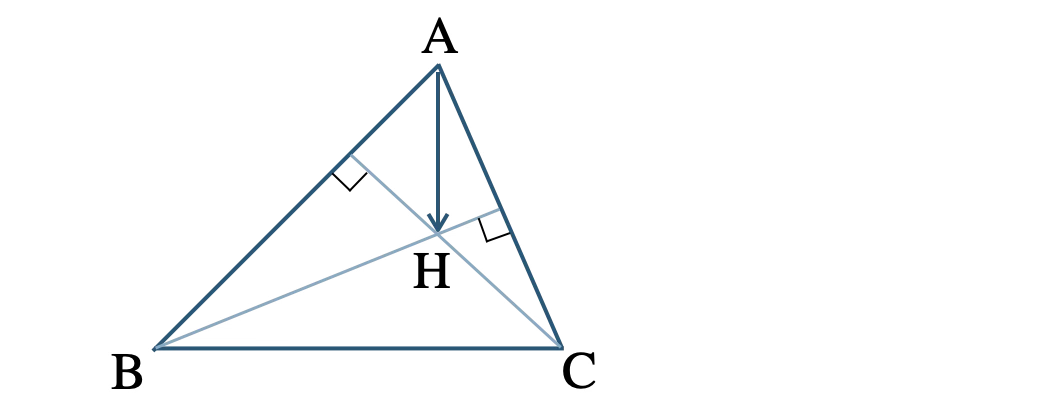
\({\rm AH \perp BC}~\Leftrightarrow ~ \overrightarrow{\rm AH}\cdot\overrightarrow{\rm BC}=0\) が目標
よって、\(\overrightarrow{\rm AH}\) と \(\overrightarrow{\rm BC}\) の内積を求める。
① 2つの基本ベクトルと 点 \({\rm H}\) を位置ベクトルでおく。
\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}~,~\overrightarrow{\rm AH}=\overrightarrow{h}\)
② 垂線の条件より、内積が \(0\) の条件式を立てる。
\(\overrightarrow{\rm BH}\perp\overrightarrow{\rm AC}\) より、\(\overrightarrow{\rm BH}\cdot\overrightarrow{\rm AC}=0\)
\(\overrightarrow{\rm CH}\perp\overrightarrow{\rm AB}\) より、\(\overrightarrow{\rm CH}\cdot\overrightarrow{\rm AB}=0\)
③ 内積 \(\overrightarrow{\rm AH}\cdot\overrightarrow{\rm BC}\) を計算して、\(0\) となることを示す。
\(\overrightarrow{\rm AH}\cdot\overrightarrow{\rm BC}=0\) より、\(\rm AH \perp BC\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|垂直に交わることの証明(三角形の垂心)
平面上のベクトル 51
\(\triangle {\rm ABC}\) の頂点 \(\rm B~,~ C\) から対辺に下ろした垂線の交点を \(\rm H\) とするとき、\(\rm AH \perp BC\) であることの証明方法は?
高校数学C|平面上のベクトル
[証明]
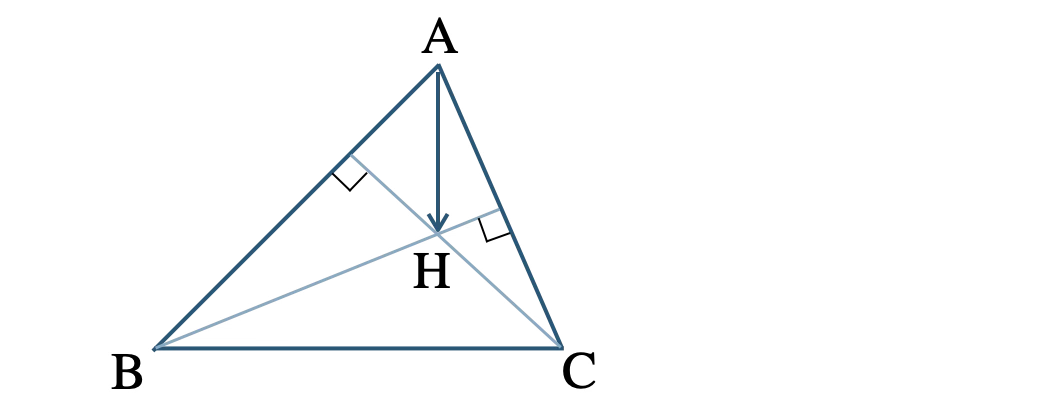
\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}~,~\overrightarrow{\rm AH}=\overrightarrow{h}\) とおくと、
\(\overrightarrow{\rm BH}\perp\overrightarrow{\rm AC}\) より、内積は \(0\) となるので、
\(\begin{eqnarray}~~~\overrightarrow{\rm BH}\cdot\overrightarrow{\rm AC}&=&0
\\[5pt]~~~(\overrightarrow{h}-\overrightarrow{b})\cdot\overrightarrow{c}&=&0
\\[5pt]~~~\overrightarrow{h}\cdot\overrightarrow{c}-\overrightarrow{b}\cdot\overrightarrow{c}&=&0
\\[5pt]~~~\overrightarrow{h}\cdot\overrightarrow{c}&=&\overrightarrow{b}\cdot\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
\(\overrightarrow{\rm CH}\perp\overrightarrow{\rm AB}\) より、内積は \(0\) となるので、
\(\begin{eqnarray}~~~\overrightarrow{\rm CH}\cdot\overrightarrow{\rm AB}&=&0
\\[5pt]~~~(\overrightarrow{h}-\overrightarrow{c})\cdot\overrightarrow{b}&=&0
\\[5pt]~~~\overrightarrow{h}\cdot\overrightarrow{b}-\overrightarrow{c}\cdot\overrightarrow{b}&=&0
\\[5pt]~~~\overrightarrow{h}\cdot\overrightarrow{b}&=&\overrightarrow{b}\cdot\overrightarrow{c}~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
ここで、\(\overrightarrow{\rm AH}\) と \(\overrightarrow{\rm BC}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AH}\cdot\overrightarrow{\rm BC}&=&\overrightarrow{h}\cdot(\overrightarrow{c}-\overrightarrow{b})
\\[5pt]~~~&=&\overrightarrow{h}\cdot\overrightarrow{c}-\overrightarrow{h}\cdot\overrightarrow{b}\end{eqnarray}\)
\(\small [\,1\,]\) と \(\small [\,2\,]\) を代入すると、
\(\begin{eqnarray}\hspace{37pt}~~~&=&\overrightarrow{b}\cdot\overrightarrow{c}-\overrightarrow{b}\cdot\overrightarrow{c}
\\[5pt]~~~&=&0
\end{eqnarray}\)
\(\overrightarrow{\rm AH}\neq\overrightarrow{0}~,~\overrightarrow{\rm BC}\neq\overrightarrow{0}\) より、\(\overrightarrow{\rm AH}\perp \overrightarrow{\rm BC}\)
したがって、\(\rm AH\perp BC\) [終]



