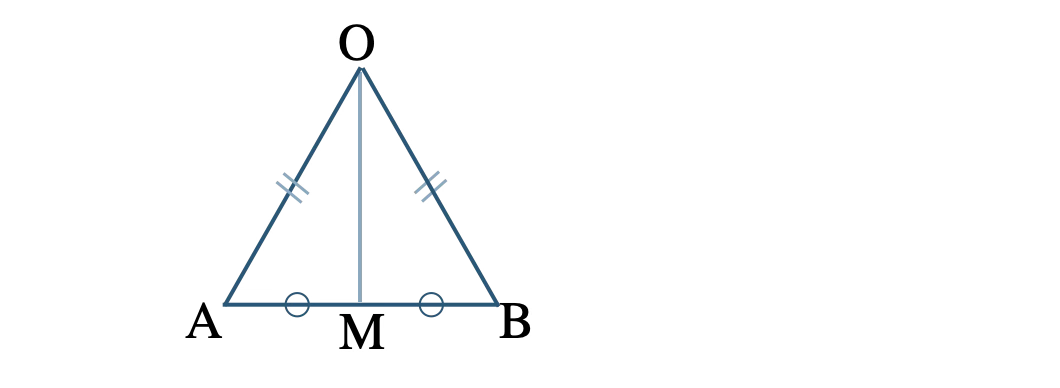このページは、「垂直に交わることの証明(三角形の垂心)」の練習問題アーカイブページとなります。
この問題の解き方の詳細は↓
垂直に交わることの証明(三角形の垂心) で確認できます。
問題アーカイブ01
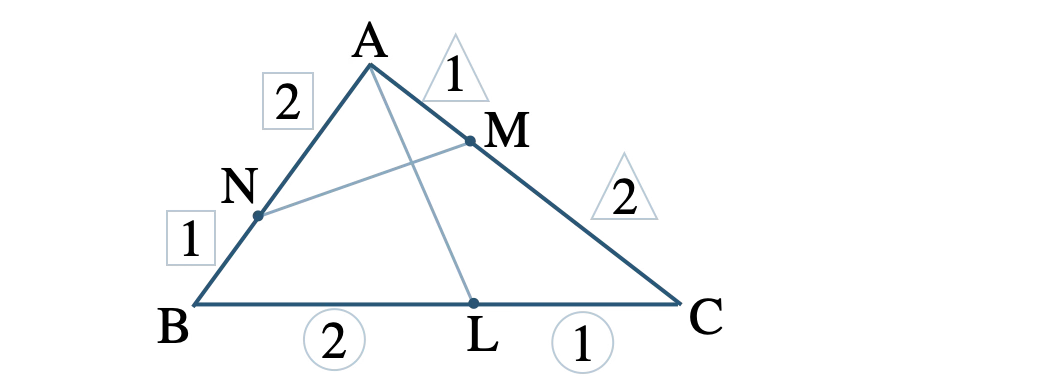
問題アーカイブ01\(\angle {\rm A}\) が直角である直角二等辺三角形 \({\rm ABC}\) の \(3\) つの辺 \({\rm BC}~,~{\rm CA}~,~{\rm AB}\) を \(2:1\) に内分する点を、それぞれ \({\rm L}~,~{\rm M}~,~{\rm N}\) とすると、\({\rm AL}\perp{\rm MN}\) であることを証明せよ。
数研出版|数学C[708] p.37 練習27
[証明]
\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) とおくと、
\(\triangle {\rm ABC}\) は \(\angle {\rm A}=90°\) の直角二等辺三角形より、
\(\overrightarrow{b}\cdot\overrightarrow{c}=0~,~|\overrightarrow{b}|=|\overrightarrow{c}|~ ~ ~ \cdots {\small [\,1\,]}\)
点 \({\rm N}\) は辺 \({\rm AB}\) を \(2:1\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AN}&=&\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{\rm AB}\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}\end{eqnarray}\)
点 \({\rm M}\) は辺 \({\rm CA}\) を \(2:1\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AM}&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{\rm AC}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c}\end{eqnarray}\)
点 \({\rm L}\) は辺 \({\rm BC}\) を \(2:1\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AL}&=&\displaystyle \frac{\,1\cdot\overrightarrow{\rm AB}+2\cdot\overrightarrow{\rm AC}\,}{\,2+1\,}\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{b}+2\overrightarrow{c}\,}{\,3\,}\end{eqnarray}\)
よって、\(\overrightarrow{\rm MN}\) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm MN}&=&\overrightarrow{\rm AN}-\overrightarrow{\rm AM}\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}-\frac{\,1\,}{\,3\,}\overrightarrow{c}\\[5pt]~~~&=&\displaystyle \frac{\,2\overrightarrow{b}-\overrightarrow{c}\,}{\,3\,}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm AL}\) と \(\overrightarrow{\rm MN}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AL}\cdot\overrightarrow{\rm MN}&=&\displaystyle \frac{\,\overrightarrow{b}+2\overrightarrow{c}\,}{\,3\,}\cdot\frac{\,2\overrightarrow{b}-\overrightarrow{c}\,}{\,3\,}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,9\,}(\overrightarrow{b}+2\overrightarrow{c})\cdot(2\overrightarrow{b}-\overrightarrow{c})\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,9\,}(2|\overrightarrow{b}|^2-\overrightarrow{b}\cdot\overrightarrow{c}+4\overrightarrow{b}\cdot\overrightarrow{c}-2|\overrightarrow{c}|^2)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,9\,}(2|\overrightarrow{b}|^2+3\overrightarrow{b}\cdot\overrightarrow{c}-2|\overrightarrow{c}|^2)\end{eqnarray}\)
\({\small [\,1\,]}\) を代入すると、
\(\begin{eqnarray}\hspace{37pt}~~~&=&\displaystyle \frac{\,1\,}{\,9\,}(2|\overrightarrow{b}|^2+0-2|\overrightarrow{b}|^2)\\[5pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm AL}\neq\overrightarrow{0}~,~\overrightarrow{\rm MN}\neq\overrightarrow{0}\) より、\(\overrightarrow{\rm AL}\perp \overrightarrow{\rm MN}\)
したがって、\({\rm AL}\perp {\rm MN}\) [終]
問題アーカイブ02
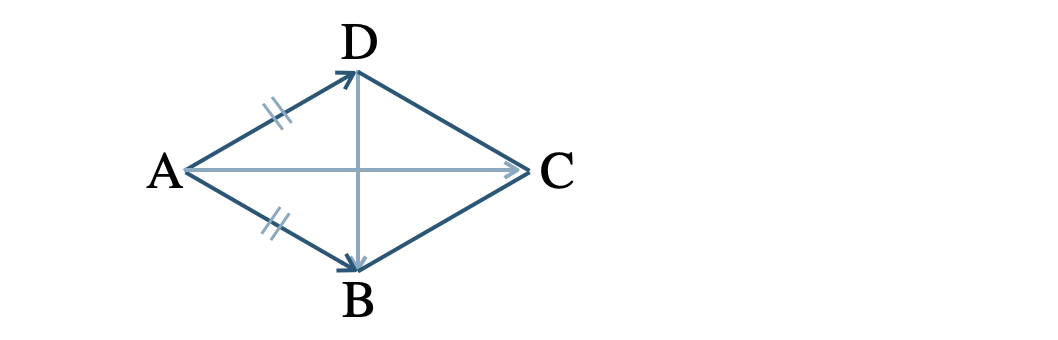
問題アーカイブ02平行四辺形 \({\rm ABCD}\) において、\({\rm AB}={\rm AD}\) のとき、\({\rm AC}\perp{\rm DB}\) である。このことを、ベクトルを用いて証明せよ。
数研出版|高等学校数学C[709] p.38 練習32
数研出版|新編数学C[710] p.39 練習33
[証明]
\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AD}=\overrightarrow{d}\) とおくと、
\({\rm AB}={\rm AD}\) より、
\(|\overrightarrow{b}|=|\overrightarrow{d}|~ ~ ~ \cdots {\small [\,1\,]}\)
四角形 \({\rm ABCD}\) は平行四辺形より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AC}&=&\overrightarrow{\rm AB}+\overrightarrow{\rm AD}\\[5pt]~~~&=&\overrightarrow{b}+\overrightarrow{d}\end{eqnarray}\)
\(\begin{eqnarray}~~~\overrightarrow{\rm DB}&=&\overrightarrow{\rm AB}-\overrightarrow{\rm AD}\\[5pt]~~~&=&\overrightarrow{b}-\overrightarrow{d}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm AC}\) と \(\overrightarrow{\rm DB}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AC}\cdot\overrightarrow{\rm DB}&=&(\overrightarrow{b}+\overrightarrow{d})\cdot(\overrightarrow{b}-\overrightarrow{d})\\[5pt]~~~&=&|\overrightarrow{b}|^2-\overrightarrow{b}\cdot\overrightarrow{d}+\overrightarrow{d}\cdot\overrightarrow{b}-|\overrightarrow{d}|^2\\[5pt]~~~&=&|\overrightarrow{b}|^2-|\overrightarrow{d}|^2\end{eqnarray}\)
\({\small [\,1\,]}\) を代入すると、
\(\begin{eqnarray}\hspace{37pt}~~~&=&|\overrightarrow{b}|^2-|\overrightarrow{b}|^2\\[5pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm AC}\neq\overrightarrow{0}~,~\overrightarrow{\rm DB}\neq\overrightarrow{0}\) より、\(\overrightarrow{\rm AC}\perp \overrightarrow{\rm DB}\)
したがって、\({\rm AC}\perp {\rm DB}\) [終]
問題アーカイブ03
問題アーカイブ03\({\rm OA}={\rm OB}\) である二等辺三角形 \({\rm OAB}\) において、底辺 \({\rm AB}\) の中点を \({\rm M}\) とする。このとき、\({\rm OM}\perp{\rm AB}\) であることを証明せよ。
東京書籍|Advanced数学C[701] p.33 問8
[証明]
\(\overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}\) とおくと、
\({\rm OA}={\rm OB}\) より、
\(|\overrightarrow{a}|=|\overrightarrow{b}|~ ~ ~ \cdots {\small [\,1\,]}\)
点 \({\rm M}\) は辺 \({\rm AB}\) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,\overrightarrow{\rm OA}+\overrightarrow{\rm OB}\,}{\,2\,}\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{b}\,}{\,2\,}\end{eqnarray}\)
また、\(\overrightarrow{\rm AB}\) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AB}&=&\overrightarrow{\rm OB}-\overrightarrow{\rm OA}\\[5pt]~~~&=&\overrightarrow{b}-\overrightarrow{a}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm OM}\) と \(\overrightarrow{\rm AB}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}\cdot\overrightarrow{\rm AB}&=&\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{b}\,}{\,2\,}\cdot(\overrightarrow{b}-\overrightarrow{a})\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{b}-\overrightarrow{a})\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{a}\cdot\overrightarrow{b}-|\overrightarrow{a}|^2+|\overrightarrow{b}|^2-\overrightarrow{b}\cdot\overrightarrow{a})\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(|\overrightarrow{b}|^2-|\overrightarrow{a}|^2)\end{eqnarray}\)
\({\small [\,1\,]}\) を代入すると、
\(\begin{eqnarray}\hspace{37pt}~~~&=&\displaystyle \frac{\,1\,}{\,2\,}(|\overrightarrow{a}|^2-|\overrightarrow{a}|^2)\\[5pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm OM}\neq\overrightarrow{0}~,~\overrightarrow{\rm AB}\neq\overrightarrow{0}\) より、\(\overrightarrow{\rm OM}\perp \overrightarrow{\rm AB}\)
したがって、\({\rm OM}\perp {\rm AB}\) [終]
問題アーカイブ04
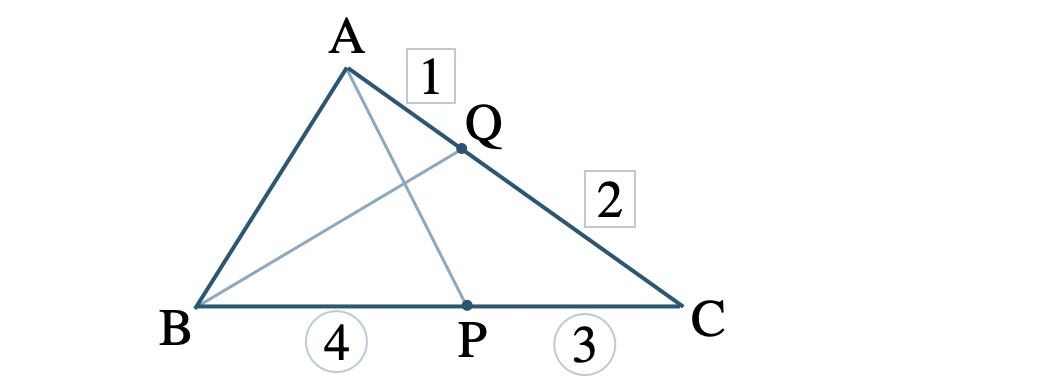
問題アーカイブ04\(\angle {\rm A}=90°\)~,~\({\rm AB}:{\rm AC}=2:3\) である \(\triangle {\rm ABC}\) において、線分 \({\rm BC}\) を \(4:3\) に内分する点を \({\rm P}\)、線分 \({\rm AC}\) を \(1:2\) に内分する点を \({\rm Q}\) とする。このとき、\({\rm AP}\perp{\rm BQ}\) であることを証明せよ。
東京書籍|Advanced数学C[701] p.33 問9
[証明]
\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) とおくと、
\(\angle {\rm A}=90°\) より、
\(\overrightarrow{b}\cdot\overrightarrow{c}=0~ ~ ~ \cdots {\small [\,1\,]}\)
\({\rm AB}:{\rm AC}=2:3\) より、
\(|\overrightarrow{c}|=\displaystyle \frac{\,3\,}{\,2\,}|\overrightarrow{b}|\)
よって、
\(|\overrightarrow{c}|^2=\displaystyle \frac{\,9\,}{\,4\,}|\overrightarrow{b}|^2~ ~ ~ \cdots {\small [\,2\,]}\)
点 \({\rm P}\) は線分 \({\rm BC}\) を \(4:3\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,3\cdot\overrightarrow{\rm AB}+4\cdot\overrightarrow{\rm AC}\,}{\,4+3\,}\\[5pt]~~~&=&\displaystyle \frac{\,3\overrightarrow{b}+4\overrightarrow{c}\,}{\,7\,}\end{eqnarray}\)
点 \({\rm Q}\) は線分 \({\rm AC}\) を \(1:2\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AQ}&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{\rm AC}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c}\end{eqnarray}\)
よって、\(\overrightarrow{\rm BQ}\) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm BQ}&=&\overrightarrow{\rm AQ}-\overrightarrow{\rm AB}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c}-\overrightarrow{b}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm AP}\) と \(\overrightarrow{\rm BQ}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}\cdot\overrightarrow{\rm BQ}&=&\displaystyle \frac{\,3\overrightarrow{b}+4\overrightarrow{c}\,}{\,7\,}\cdot\left(\frac{\,1\,}{\,3\,}\overrightarrow{c}-\overrightarrow{b}\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,7\,}(3\overrightarrow{b}+4\overrightarrow{c})\cdot\left(\frac{\,1\,}{\,3\,}\overrightarrow{c}-\overrightarrow{b}\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,7\,}\left(\overrightarrow{b}\cdot\overrightarrow{c}-3|\overrightarrow{b}|^2+\frac{\,4\,}{\,3\,}|\overrightarrow{c}|^2-4\overrightarrow{b}\cdot\overrightarrow{c}\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,7\,}\left(-3|\overrightarrow{b}|^2+\frac{\,4\,}{\,3\,}|\overrightarrow{c}|^2-3\overrightarrow{b}\cdot\overrightarrow{c}\right)\end{eqnarray}\)
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) を代入すると、
\(\begin{eqnarray}\hspace{37pt}~~~&=&\displaystyle \frac{\,1\,}{\,7\,}\left(-3|\overrightarrow{b}|^2+\frac{\,4\,}{\,3\,}\cdot\frac{\,9\,}{\,4\,}|\overrightarrow{b}|^2-0\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,7\,}(-3|\overrightarrow{b}|^2+3|\overrightarrow{b}|^2)\\[5pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm AP}\neq\overrightarrow{0}~,~\overrightarrow{\rm BQ}\neq\overrightarrow{0}\) より、\(\overrightarrow{\rm AP}\perp \overrightarrow{\rm BQ}\)
したがって、\({\rm AP}\perp {\rm BQ}\) [終]
問題アーカイブ05
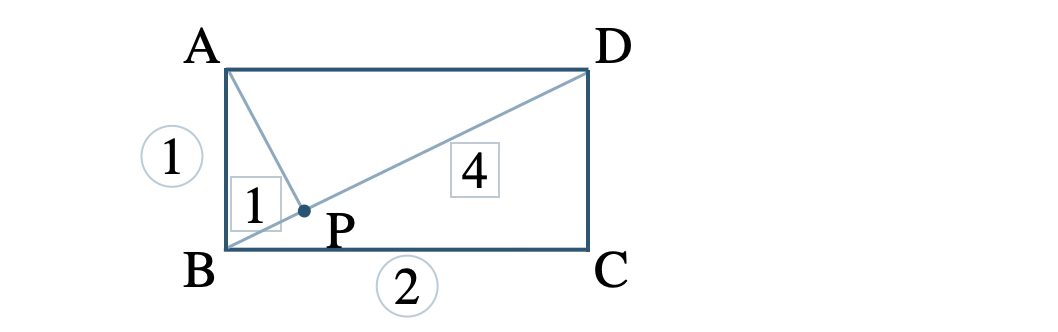
問題アーカイブ05長方形 \({\rm ABCD}\) において、\({\rm AB}=1\)~,~\({\rm BC}=2\) であるとき、対角線 \({\rm BD}\) を \(1:4\) に内分する点を \({\rm P}\) とすれば、\({\rm AP}\perp{\rm BD}\) であることを証明せよ。
東京書籍|Standard数学C[702] p.39 問6
[証明]
\(\overrightarrow{\rm BA}=\overrightarrow{a}~,~\overrightarrow{\rm BC}=\overrightarrow{c}\) とおくと、
四角形 \({\rm ABCD}\) は長方形より、
\(\overrightarrow{a}\cdot\overrightarrow{c}=0~ ~ ~ \cdots {\small [\,1\,]}\)
\({\rm AB}=1\) より、
\(|\overrightarrow{a}|^2=1~ ~ ~ \cdots {\small [\,2\,]}\)
\({\rm BC}=2\) より、
\(|\overrightarrow{c}|^2=4~ ~ ~ \cdots {\small [\,3\,]}\)
長方形より、\(\overrightarrow{\rm BD}\) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm BD}&=&\overrightarrow{\rm BA}+\overrightarrow{\rm AD}\\[5pt]~~~&=&\overrightarrow{a}+\overrightarrow{c}\end{eqnarray}\)
点 \({\rm P}\) は対角線 \({\rm BD}\) を \(1:4\) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm BP}&=&\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{\rm BD}\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{c}\,}{\,5\,}\end{eqnarray}\)
よって、\(\overrightarrow{\rm AP}\) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\overrightarrow{\rm AB}+\overrightarrow{\rm BP}\\[5pt]~~~&=&-\overrightarrow{a}+\displaystyle \frac{\,\overrightarrow{a}+\overrightarrow{c}\,}{\,5\,}\\[5pt]~~~&=&\displaystyle \frac{\,-5\overrightarrow{a}+\overrightarrow{a}+\overrightarrow{c}\,}{\,5\,}\\[5pt]~~~&=&\displaystyle \frac{\,-4\overrightarrow{a}+\overrightarrow{c}\,}{\,5\,}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm AP}\) と \(\overrightarrow{\rm BD}\) の内積は、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}\cdot\overrightarrow{\rm BD}&=&\displaystyle \frac{\,-4\overrightarrow{a}+\overrightarrow{c}\,}{\,5\,}\cdot(\overrightarrow{a}+\overrightarrow{c})\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,5\,}(-4\overrightarrow{a}+\overrightarrow{c})\cdot(\overrightarrow{a}+\overrightarrow{c})\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,5\,}(-4|\overrightarrow{a}|^2-4\overrightarrow{a}\cdot\overrightarrow{c}+\overrightarrow{a}\cdot\overrightarrow{c}+|\overrightarrow{c}|^2)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,5\,}(-4|\overrightarrow{a}|^2+|\overrightarrow{c}|^2-3\overrightarrow{a}\cdot\overrightarrow{c})\end{eqnarray}\)
\({\small [\,1\,]}~,~{\small [\,2\,]}~,~{\small [\,3\,]}\) を代入すると、
\(\begin{eqnarray}\hspace{37pt}~~~&=&\displaystyle \frac{\,1\,}{\,5\,}(-4\cdot 1+4-0)\\[5pt]~~~&=&0\end{eqnarray}\)
\(\overrightarrow{\rm AP}\neq\overrightarrow{0}~,~\overrightarrow{\rm BD}\neq\overrightarrow{0}\) より、\(\overrightarrow{\rm AP}\perp \overrightarrow{\rm BD}\)
したがって、\({\rm AP}\perp {\rm BD}\) [終]