- 数学C｜平面上のベクトル「ベクトルの等式と点の位置」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題｜ベクトルの等式と点の位置
平面上のベクトル 52\(\triangle {\rm ABC}\) と点 \(\rm P\) について、等式 \(5\overrightarrow{\rm PA}+4\overrightarrow{\rm PB}+3\overrightarrow{\rm PC}=\overrightarrow{0}\) が成り立つときの点 \(\rm P\) の位置の調べ方は？また、\(\triangle {\rm PBC}:\triangle {\rm PCA}:\triangle {\rm PAB}\) の求め方は？
高校数学C｜平面上のベクトル
解法のPoint
ベクトルの等式と点の位置
Point：ベクトルの等式と点の位置
① 与えられた等式の始点を \({\rm A}\) からにして、\(\overrightarrow{\rm AP}\) を基本ベクトルで表す。
\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) として、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,4\overrightarrow{b}+3\overrightarrow{c}\,}{\,12\,}\end{eqnarray}\)
② 分子の係数の和を分母分子にかけて、実数倍×内分のベクトルの形に式変形する。
\(4+3=7\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,7\,}{\,12\,}{\, \small \times \,}\frac{\,4\overrightarrow{b}+3\overrightarrow{c}\,}{\,7\,}
\end{eqnarray}\)
③ 辺 \({\rm BC}\) の内分点を \({\rm D}\) として、点 \({\rm P}\) の位置を調べる。
\(\overrightarrow{\rm AD}=\displaystyle \frac{\,4\overrightarrow{b}+3\overrightarrow{c}\,}{\,3+4\,}\) より、\(\overrightarrow{\rm AP}=\displaystyle \frac{\,7\,}{\,12\,}\,\overrightarrow{\rm AD}\)
よって、
\({\rm BD}:{\rm DC}=3:4~,~{\rm AP}:{\rm PD}=7:5\)
ベクトルの等式 \(5\overrightarrow{\rm PA}+4\overrightarrow{\rm PB}+3\overrightarrow{\rm PC}=\overrightarrow{0}\) より、点 \({\rm P}\) の位置の調べ方は、
① 与えられた等式の始点を \({\rm A}\) からにして、\(\overrightarrow{\rm AP}\) を基本ベクトルで表す。
\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) として、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,4\overrightarrow{b}+3\overrightarrow{c}\,}{\,12\,}\end{eqnarray}\)
② 分子の係数の和を分母分子にかけて、実数倍×内分のベクトルの形に式変形する。
\(4+3=7\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,7\,}{\,12\,}{\, \small \times \,}\frac{\,4\overrightarrow{b}+3\overrightarrow{c}\,}{\,7\,}
\end{eqnarray}\)
③ 辺 \({\rm BC}\) の内分点を \({\rm D}\) として、点 \({\rm P}\) の位置を調べる。
\(\overrightarrow{\rm AD}=\displaystyle \frac{\,4\overrightarrow{b}+3\overrightarrow{c}\,}{\,3+4\,}\) より、\(\overrightarrow{\rm AP}=\displaystyle \frac{\,7\,}{\,12\,}\,\overrightarrow{\rm AD}\)
よって、
\({\rm BD}:{\rm DC}=3:4~,~{\rm AP}:{\rm PD}=7:5\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説｜ベクトルの等式と点の位置
平面上のベクトル 52
\(\triangle {\rm ABC}\) と点 \(\rm P\) について、等式 \(5\overrightarrow{\rm PA}+4\overrightarrow{\rm PB}+3\overrightarrow{\rm PC}=\overrightarrow{0}\) が成り立つときの点 \(\rm P\) の位置の調べ方は？また、\(\triangle {\rm PBC}:\triangle {\rm PCA}:\triangle {\rm PAB}\) の求め方は？
高校数学C｜平面上のベクトル
\(5\overrightarrow{\rm PA}+4\overrightarrow{\rm PB}+3\overrightarrow{\rm PC}=\overrightarrow{0}\) の始点を \({\rm A}\) からにすると、
\(\begin{eqnarray}~5\overrightarrow{\rm PA}+4\overrightarrow{\rm PB}+3\overrightarrow{\rm PC}&=&\overrightarrow{0}
\\[5pt]~5(-\overrightarrow{\rm AP})+4(\overrightarrow{\rm AB}-\overrightarrow{\rm AP})+3(\overrightarrow{\rm AC}-\overrightarrow{\rm AP})&=&\overrightarrow{0}
\\[5pt]~-5\overrightarrow{\rm AP}+4\overrightarrow{\rm AB}-4\overrightarrow{\rm AP}+3\overrightarrow{\rm AC}-3\overrightarrow{\rm AP}&=&\overrightarrow{0}
\end{eqnarray}\)
\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) とおくと、
\(\begin{eqnarray}~~~-12\overrightarrow{\rm AP}+4\overrightarrow{b}+3\overrightarrow{c}&=&\overrightarrow{0}
\\[5pt]~~~-12\overrightarrow{\rm AP}&=&-4\overrightarrow{b}-3\overrightarrow{c}
\\[5pt]~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,4\overrightarrow{b}+3\overrightarrow{c}\,}{\,12\,}
\end{eqnarray}\)
分子の係数の和 \(4+3=7\) を分母分子にかけて、実数倍×内分のベクトルの形に式変形すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,7\,}{\,7\,}{\, \small \times \,}\frac{\,4\overrightarrow{b}+3\overrightarrow{c}\,}{\,12\,}
\\[5pt]~~~&=&\displaystyle \frac{\,7\,}{\,12\,}{\, \small \times \,}\frac{\,4\overrightarrow{b}+3\overrightarrow{c}\,}{\,3+4\,}
\end{eqnarray}\)
ここで、辺 \({\rm BC}\) を \(3:4\) に内分する点を \({\rm D}\) とすると、\(\overrightarrow{\rm AD}=\displaystyle \frac{\,4\overrightarrow{b}+3\overrightarrow{c}\,}{\,3+4\,}\) となるので、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,7\,}{\,12\,}\,\overrightarrow{\rm AD}
\end{eqnarray}\)
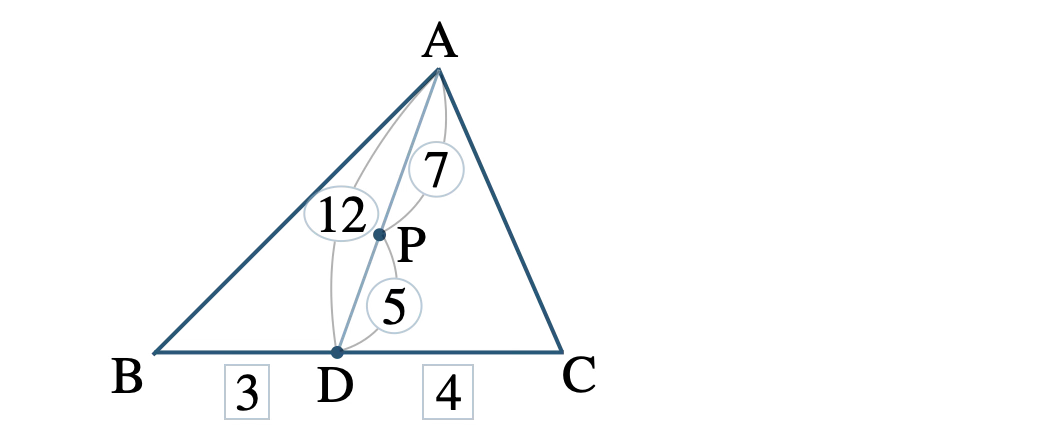
したがって、
点 \({\rm P}\) は、点 \({\rm A}\) と辺 \({\rm BC}\) を \(3:4\) に内分する点 \({\rm D}\) を結んだ線分 \({\rm AD}\) を \(7:5\) に内分する点である
また、\({\rm BD}:{\rm DC}=3:4~,~{\rm AP}:{\rm PD}=7:5\) であるので、\(\triangle {\rm ABC}\) の面積を \(S\) とすると、
\(\begin{eqnarray}~~~\triangle {\rm ABD}&=&\displaystyle \frac{\,3\,}{\,3+4\,}S~=~\frac{\,3\,}{\,7\,}S
\\[5pt]~~~\triangle {\rm ADC}&=&\displaystyle \frac{\,4\,}{\,3+4\,}S~=~\frac{\,4\,}{\,7\,}S
\end{eqnarray}\)
点 \({\rm P}\) は線分 \({\rm AD}\) を \(7:5\) に内分する点であるので、
\(\begin{eqnarray}~~~\triangle {\rm PAB}&=&\displaystyle \frac{\,7\,}{\,12\,}\triangle {\rm ABD}~=~\frac{\,7\,}{\,12\,}{\, \small \times \,}\frac{\,3\,}{\,7\,}S~=~\frac{\,1\,}{\,4\,}S
\\[5pt]~~~\triangle {\rm PCA}&=&\displaystyle \frac{\,7\,}{\,12\,}\triangle {\rm ADC}~=~\frac{\,7\,}{\,12\,}{\, \small \times \,}\frac{\,4\,}{\,7\,}S~=~\frac{\,1\,}{\,3\,}S
\\[5pt]~~~\triangle {\rm PBC}&=&\displaystyle \frac{\,5\,}{\,7+5\,}{\triangle {\rm ABC}}~=~\frac{\,5\,}{\,12\,}S
\end{eqnarray}\)
\\[5pt]~~~\triangle {\rm PCA}&=&\displaystyle \frac{\,7\,}{\,12\,}\triangle {\rm ADC}~=~\frac{\,7\,}{\,12\,}{\, \small \times \,}\frac{\,4\,}{\,7\,}S~=~\frac{\,1\,}{\,3\,}S
\\[5pt]~~~\triangle {\rm PBC}&=&\displaystyle \frac{\,5\,}{\,7+5\,}{\triangle {\rm ABC}}~=~\frac{\,5\,}{\,12\,}S
\end{eqnarray}\)
したがって、
\(\begin{eqnarray}~~~&&\triangle {\rm PBC}:\triangle {\rm PCA}:\triangle {\rm PAB}\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,12\,}S:\frac{\,1\,}{\,3\,}S:\frac{\,1\,}{\,4\,}S\\[5pt]~~~&=&5:4:3
\end{eqnarray}\)
