- 数学C|平面上のベクトル「中線定理のベクトルでの証明」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|中線定理のベクトルでの証明
平面上のベクトル 54☆\(\triangle {\rm ABC}\) の辺 \({\rm BC}\) の中点を \({\rm M}\) として、\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) とするとき、等式 \({\rm AB^2+AC^2=2(AM^2+BM^2)}\) が成り立つことの証明方法は?
高校数学C|平面上のベクトル
解法のPoint
中線定理のベクトルでの証明
Point:中線定理のベクトルでの証明

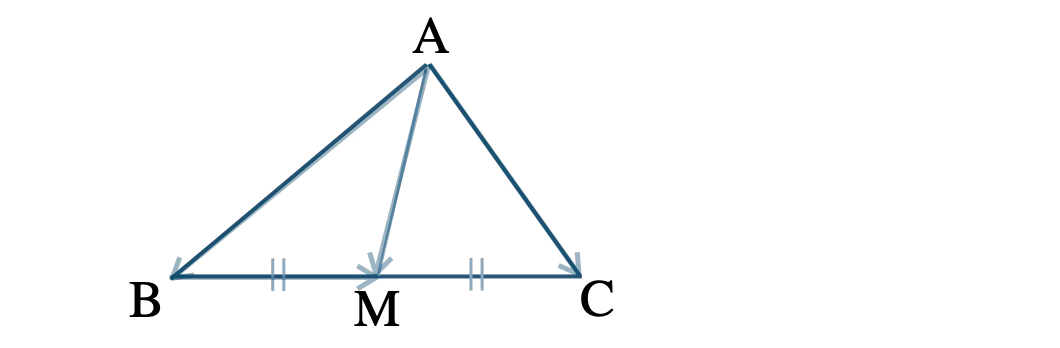
① 基本となる2つのベクトルをおく。
\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\)
② それぞれのベクトルの大きさの2乗を①の位置ベクトルで表す。
\(| \overrightarrow{\rm AB} |^2~,~| \overrightarrow{\rm AC} |^2~,~| \overrightarrow{\rm AM} |^2~,~| \overrightarrow{\rm BM} |^2\)
③ 両式をそれぞれ計算して、等しいことを示す。
\(\begin{eqnarray}~~~| \overrightarrow{\rm AB} |^2+| \overrightarrow{\rm AC} |^2=2( | \overrightarrow{\rm AM} |^2+| \overrightarrow{\rm BM} |^2 )
\end{eqnarray}\)
中線定理のベクトルによる証明の手順は、


① 基本となる2つのベクトルをおく。
\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\)
② それぞれのベクトルの大きさの2乗を①の位置ベクトルで表す。
\(| \overrightarrow{\rm AB} |^2~,~| \overrightarrow{\rm AC} |^2~,~| \overrightarrow{\rm AM} |^2~,~| \overrightarrow{\rm BM} |^2\)
③ 両式をそれぞれ計算して、等しいことを示す。
\(\begin{eqnarray}~~~| \overrightarrow{\rm AB} |^2+| \overrightarrow{\rm AC} |^2=2( | \overrightarrow{\rm AM} |^2+| \overrightarrow{\rm BM} |^2 )
\end{eqnarray}\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|中線定理のベクトルでの証明
平面上のベクトル 54☆
\(\triangle {\rm ABC}\) の辺 \({\rm BC}\) の中点を \({\rm M}\) として、\(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) とするとき、等式 \({\rm AB^2+AC^2=2(AM^2+BM^2)}\) が成り立つことの証明方法は?
高校数学C|平面上のベクトル
[証明] \(\overrightarrow{\rm AB}=\overrightarrow{b}~,~\overrightarrow{\rm AC}=\overrightarrow{c}\) より、
\(\begin{eqnarray}~~~| \overrightarrow{\rm AB} |^2+| \overrightarrow{\rm AC} |^2=| \overrightarrow{b} |^2+| \overrightarrow{c} |^2~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、\( \overrightarrow{\rm AM} \) は中点の公式より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AM}&=&\displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{c}\,}{\,2\,}
\end{eqnarray}\)
これより、
\(\begin{eqnarray}~~~| \overrightarrow{\rm AM} |^2
&=&\left| \displaystyle \frac{\,\overrightarrow{b}+\overrightarrow{c}\,}{\,2\,} \right|^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,| \overrightarrow{b}+\overrightarrow{c} |^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,(\overrightarrow{b}+\overrightarrow{c})\cdot(\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,( | \overrightarrow{b} |^2 + 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{c} |^2 )
\end{eqnarray}\)
次に、\( \overrightarrow{\rm BM}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm BC} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm BM}&=&\displaystyle \frac{\,1\,}{\,2\,}(\overrightarrow{c}-\overrightarrow{b})
\end{eqnarray}\)
よって、
\(\begin{eqnarray}~~~| \overrightarrow{\rm BM} |^2
&=&\left| \displaystyle \frac{\,\overrightarrow{c}-\overrightarrow{b}\,}{\,2\,} \right|^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,| \overrightarrow{c}-\overrightarrow{b} |^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,(\overrightarrow{c}-\overrightarrow{b})\cdot(\overrightarrow{c}-\overrightarrow{b})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\,( | \overrightarrow{c} |^2 – 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{b} |^2 )
\end{eqnarray}\)
以上より、右辺は、
\(\begin{eqnarray}~~~&&2( | \overrightarrow{\rm AM} |^2 + | \overrightarrow{\rm BM} |^2 )
\\[5pt]~~~&=&2 \cdot \displaystyle \frac{\,1\,}{\,4\,}\,( | \overrightarrow{b} |^2 + 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{c} |^2+ | \overrightarrow{c} |^2 – 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{b} |^2 )
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\,( 2\,| \overrightarrow{b} |^2 + 2\,| \overrightarrow{c} |^2 )
\\[5pt]~~~&=&| \overrightarrow{b} |^2 + | \overrightarrow{c} |^2~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\\[5pt]~~~&=&2 \cdot \displaystyle \frac{\,1\,}{\,4\,}\,( | \overrightarrow{b} |^2 + 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{c} |^2+ | \overrightarrow{c} |^2 – 2\,\overrightarrow{b}\cdot\overrightarrow{c} + | \overrightarrow{b} |^2 )
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\,( 2\,| \overrightarrow{b} |^2 + 2\,| \overrightarrow{c} |^2 )
\\[5pt]~~~&=&| \overrightarrow{b} |^2 + | \overrightarrow{c} |^2~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
よって、\(\small [\,1\,]\) と \(\small [\,2\,]\) より、
\(\begin{eqnarray}~~~| \overrightarrow{\rm AB} |^2+| \overrightarrow{\rm AC} |^2=2( | \overrightarrow{\rm AM} |^2+| \overrightarrow{\rm BM} |^2 )
\end{eqnarray}\)
したがって、\({\rm AB^2+AC^2=2(AM^2+BM^2)}\) [終]



