- 数学C|平面上のベクトル「係数の和が一定の値の点の存在範囲」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|係数の和が一定の値の点の存在範囲
平面上のベクトル 57\(\triangle {\rm OAB}\) に対して、点 \(\rm P\) が等式 \(\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}~,~s+t=2~,~\)\(s {\small ~≧~} 0~,~ t {\small ~≧~} 0\) を満たすときの点 \(\rm P\) の存在範囲の求め方は?
高校数学C|平面上のベクトル
解法のPoint
条件式を満たす点の存在範囲
Point:条件式を満たす点の存在範囲
\(\small [\,1\,]\,\,\) \(\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}~,~s+t=1\)
このとき、点 \(\rm P\) の存在範囲は直線 \({\rm AB}\) となる。
このとき、点 \(\rm P\) の存在範囲は線分 \({\rm AB}\) となる。
\(\triangle {\rm OAB}\) に対して、点 \(\rm P\) が
\(\small [\,1\,]\,\,\) \(\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}~,~s+t=1\)
このとき、点 \(\rm P\) の存在範囲は直線 \({\rm AB}\) となる。
\(\small [\,2\,]\) \(\begin{eqnarray}&&\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}
\\[2pt]&&s+t=1~,~s{\small ~≧~}0~,~t{\small ~≧~}0\end{eqnarray}\)
このとき、点 \(\rm P\) の存在範囲は線分 \({\rm AB}\) となる。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
係数の和が一定の値の点の存在範囲
Point:係数の和が一定の値の点の存在範囲係数の和が一定の値をとる点の存在範囲は、
\(\begin{eqnarray}&&\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}
\\[3pt]&&s+t=2~,~s{\small ~≧~}0~,~t{\small ~≧~}0\end{eqnarray}\)
のとき、
① 係数の和の式の右辺が \(1\) となるように、\(s^{\prime}~,~t^{\prime}\) をおく。
\(s+t=2\) より、\(\displaystyle \frac{\,s\,}{\,2\,}+\displaystyle \frac{\,t\,}{\,2\,}=1\) となり、
\(\displaystyle \frac{\,s\,}{\,2\,}=s^{\prime}~,~\displaystyle \frac{\,t\,}{\,2\,}=t^{\prime}\) とおくと、
\(s^{\prime}+t^{\prime}=1~,~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\)
② ベクトル \(\overrightarrow{\rm OP}\) の式の係数が \(s^{\prime}~,~t^{\prime}\) となるように、新たな点 \({\rm A^{\prime}~,~B^{\prime}}\) をとる。
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}
\\[3pt]~~~&=&s^{\prime}(2\overrightarrow{\rm OA})+t^{\prime}(2\overrightarrow{\rm OB})
\\[3pt]~~~&=&s^{\prime}\overrightarrow{\rm OA^{\prime}}+t^{\prime}\overrightarrow{\rm OB^{\prime}}
\end{eqnarray}\)
③ 新たな点 \({\rm A^{\prime}~,~B^{\prime}}\) を用いて、点 \(\rm P\) の存在範囲を求める。
\(\begin{eqnarray}&&\overrightarrow{\rm OP}=s^{\prime}\overrightarrow{\rm OA^{\prime}}+t^{\prime}\overrightarrow{\rm OB^{\prime}}
\\[3pt]&&s^{\prime}+t^{\prime}=1~,~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\end{eqnarray}\)


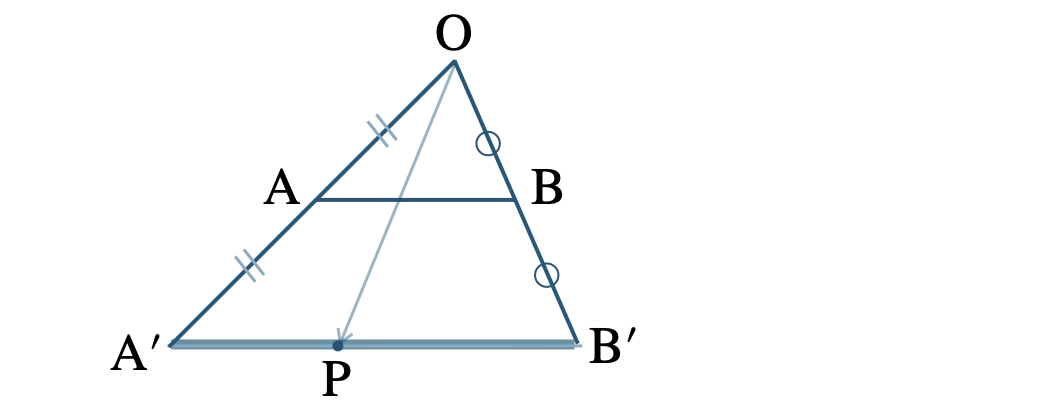
点 \(\rm P\) の存在範囲は線分 \(\rm A^{\prime}B^{\prime}\)
\(\begin{eqnarray}&&\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}
\\[3pt]&&s+t=2~,~s{\small ~≧~}0~,~t{\small ~≧~}0\end{eqnarray}\)
のとき、
① 係数の和の式の右辺が \(1\) となるように、\(s^{\prime}~,~t^{\prime}\) をおく。
\(s+t=2\) より、\(\displaystyle \frac{\,s\,}{\,2\,}+\displaystyle \frac{\,t\,}{\,2\,}=1\) となり、
\(\displaystyle \frac{\,s\,}{\,2\,}=s^{\prime}~,~\displaystyle \frac{\,t\,}{\,2\,}=t^{\prime}\) とおくと、
\(s^{\prime}+t^{\prime}=1~,~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\)
② ベクトル \(\overrightarrow{\rm OP}\) の式の係数が \(s^{\prime}~,~t^{\prime}\) となるように、新たな点 \({\rm A^{\prime}~,~B^{\prime}}\) をとる。
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}
\\[3pt]~~~&=&s^{\prime}(2\overrightarrow{\rm OA})+t^{\prime}(2\overrightarrow{\rm OB})
\\[3pt]~~~&=&s^{\prime}\overrightarrow{\rm OA^{\prime}}+t^{\prime}\overrightarrow{\rm OB^{\prime}}
\end{eqnarray}\)
③ 新たな点 \({\rm A^{\prime}~,~B^{\prime}}\) を用いて、点 \(\rm P\) の存在範囲を求める。
\(\begin{eqnarray}&&\overrightarrow{\rm OP}=s^{\prime}\overrightarrow{\rm OA^{\prime}}+t^{\prime}\overrightarrow{\rm OB^{\prime}}
\\[3pt]&&s^{\prime}+t^{\prime}=1~,~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\end{eqnarray}\)



点 \(\rm P\) の存在範囲は線分 \(\rm A^{\prime}B^{\prime}\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|係数の和が一定の値の点の存在範囲
平面上のベクトル 57\(\triangle {\rm OAB}\) に対して、点 \(\rm P\) が等式 \(\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}~,~s+t=2~,~\)\(s {\small ~≧~} 0~,~ t {\small ~≧~} 0\) を満たすときの点 \(\rm P\) の存在範囲の求め方は?
高校数学C|平面上のベクトル
\(s+t=2\) より、右辺が \(1\) となるように式変形すると、
\(\begin{eqnarray}~~~s+t&=&2
\\[5pt]~~~\displaystyle \frac{\,s\,}{\,2\,}+\displaystyle \frac{\,t\,}{\,2\,}&=&1
\end{eqnarray}\)
ここで、 \(\displaystyle \frac{\,s\,}{\,2\,}=s^{\prime}~,~\displaystyle \frac{\,t\,}{\,2\,}=t^{\prime}\) とおくと、
\(\begin{eqnarray}~~~s^{\prime}+t^{\prime}&=&1\end{eqnarray}\)
また、\(s=2s^{\prime}~,~t=2t^{\prime}\) となり、\(s{\small ~≧~}0~,~t{\small ~≧~}0\) より、
\(\begin{eqnarray}~~~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\end{eqnarray}\)
次に、\(\overrightarrow{\rm OP}\) は、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}
\\[3pt]~~~&=&2s^{\prime}\overrightarrow{\rm OA}+2t^{\prime}\overrightarrow{\rm OB}
\\[3pt]~~~&=&s^{\prime}(2\overrightarrow{\rm OA})+t^{\prime}(2\overrightarrow{\rm OB})
\end{eqnarray}\)
ここで、\(\overrightarrow{\rm OA^{\prime}}=2\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB^{\prime}}=2\overrightarrow{\rm OB}\) を満たす点 \(\rm A^{\prime}~,~B^{\prime}\) をとると、



\(\begin{eqnarray}&&\overrightarrow{\rm OP}=s^{\prime}\overrightarrow{\rm OA^{\prime}}+t^{\prime}\overrightarrow{\rm OB^{\prime}}
\\[3pt]&&s^{\prime}+t^{\prime}=1~,~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\end{eqnarray}\)
これより、点 \(\rm P\) の存在範囲は2点 \(\rm A^{\prime}~,~B^{\prime}\) を結ぶ線分 \(\rm A^{\prime}B^{\prime}\) 上となる



