- 数学C|平面上のベクトル「0≦s≦1と0≦t≦1を満たす点の存在範囲」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|0≦s≦1と0≦t≦1を満たす点の存在範囲
平面上のベクトル 60☆\(\triangle {\rm OAB}\) に対して、点 \(\rm P\) が等式 \(\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}~,~0{\small ~≦~}s{\small ~≦~}1~,~\)\(0 {\small ~≦~}t{\small ~≦~}1\) を満たすときの点 \(\rm P\) の存在範囲の求め方は?
高校数学C|平面上のベクトル
解法のPoint
0≦s≦1と0≦t≦1を満たす点の存在範囲
Point:0≦s≦1と0≦t≦1を満たす点の存在範囲
\(\begin{eqnarray}&&\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}
\\[2pt]&&0{\small ~≦~}s{\small ~≦~}1~,~0 {\small ~≦~}t{\small ~≦~}1\end{eqnarray}\)
を満たすときの点 \(\rm P\) の存在範囲は、
① \(s\) を固定したときの点 \({\rm P}\) の存在範囲を考える。
\(\overrightarrow{\rm OP}=\overrightarrow{\rm OA^{\prime}}+t\overrightarrow{\rm OB}\) とすると、


② \(s\) が変化したとき、①がどのように動くか調べて、点 \({\rm P}\) の存在範囲を求める。



\({\rm P}\) の存在範囲は、
線分 \({\rm OA~,~OB}\) を隣り合う2辺とする
平行四辺形の周および内部となる。
\(\triangle {\rm OAB}\) に対して、
\(\begin{eqnarray}&&\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}
\\[2pt]&&0{\small ~≦~}s{\small ~≦~}1~,~0 {\small ~≦~}t{\small ~≦~}1\end{eqnarray}\)
を満たすときの点 \(\rm P\) の存在範囲は、
① \(s\) を固定したときの点 \({\rm P}\) の存在範囲を考える。
\(\overrightarrow{\rm OP}=\overrightarrow{\rm OA^{\prime}}+t\overrightarrow{\rm OB}\) とすると、



② \(s\) が変化したとき、①がどのように動くか調べて、点 \({\rm P}\) の存在範囲を求める。



\({\rm P}\) の存在範囲は、
線分 \({\rm OA~,~OB}\) を隣り合う2辺とする
平行四辺形の周および内部となる。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|0≦s≦1と0≦t≦1を満たす点の存在範囲
平面上のベクトル 60☆
\(\triangle {\rm OAB}\) に対して、点 \(\rm P\) が等式 \(\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}~,~0{\small ~≦~}s{\small ~≦~}1~,~\)\(0 {\small ~≦~}t{\small ~≦~}1\) を満たすときの点 \(\rm P\) の存在範囲の求め方は?
高校数学C|平面上のベクトル
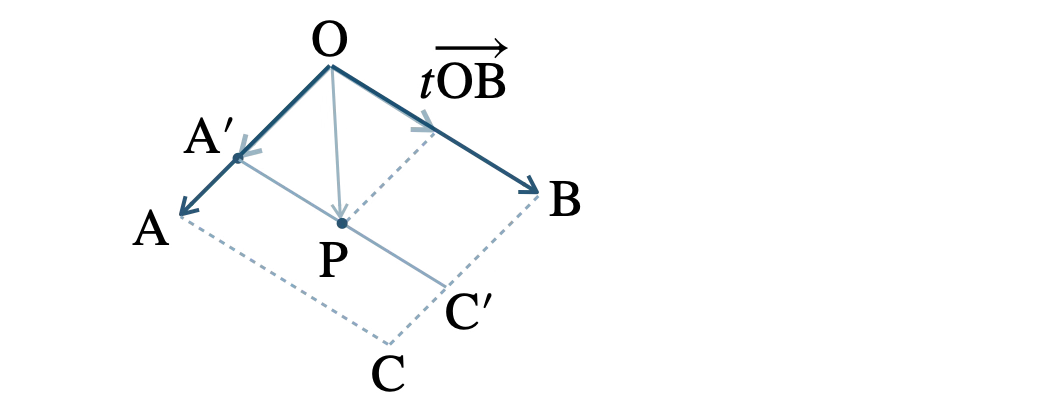
\(s\) を固定して、\(s\overrightarrow{\rm OA}=\overrightarrow{\rm OA^{\prime}}\) とすると、
\(\overrightarrow{\rm OP}=\overrightarrow{\rm OA^{\prime}}+t\overrightarrow{\rm OB}~,~0 {\small ~≦~}t{\small ~≦~}1\)



点 \({\rm P}\) は、\(t\) が \(0 {\small ~≦~}t{\small ~≦~}1\) の範囲で変化することによって、図の線分 \({\rm A^{\prime}C^{\prime}}\) 上を動く
ここで、\(s\) を \(0 {\small ~≦~}s{\small ~≦~}1\) で変化させると、
線分 \({\rm A^{\prime}C^{\prime}}\) は、\({\rm OB}\) と平行を保ちながら \({\rm AC}\) まで動く



したがって、
\({\rm P}\) の存在範囲は、
線分 \({\rm OA~,~OB}\) を隣り合う2辺とする
平行四辺形の周および内部となる



