- 数学C|平面上のベクトル「三角形の内部の点と線分の比・面積比」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|三角形の内部の点と線分の比・面積比
平面上のベクトル 61☆\(\triangle {\rm OAB}\) ( \(\overrightarrow{\rm OA}=\overrightarrow{a}~,~ \overrightarrow{\rm OB}=\overrightarrow{b}\) ) において、辺 \({\rm OA}\) の中点を \(\rm C\)、辺 \({\rm OB}\) を \(1:2\) に内分する点を \(\rm D\) 、2直線 \(\rm AD\) と \(\rm BC\) の交点 \(\rm P\)、直線 \(\rm OP\) と辺 \(\rm AB\) が交わる点を \(\rm E\) とするとき、\(\rm OP:PE\) と \(\rm AE:EB\) の求め方は?また、\(\triangle {\rm OAB}~,~\triangle {\rm PAB}~,~\triangle {\rm OAP}~,~\triangle {\rm PEB}\) の面積比の求め方は?
高校数学C|平面上のベクトル
解法のPoint
三角形の内部の点と線分の比
Point:三角形の内部の点と線分の比
① \(\overrightarrow{\rm OP}\) を位置ベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) を用いて表す。
\(\overrightarrow{\rm OP}=\displaystyle \frac{\,2\,}{\,5\,}\overrightarrow{a}
+\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{b}\)
※ 求め方は、こちらを参照してください。
② 点 \(\rm E\) は直線 \({\rm OP}\) の延長線上より、\(\overrightarrow{\rm OE}=k\,\overrightarrow{\rm OP}\) となる。
\(\begin{eqnarray}~~~\overrightarrow{\rm OE}&=&k\,\overrightarrow{\rm OP}=\displaystyle \frac{\,2\,}{\,5\,}k\,\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,5\,}k\,\overrightarrow{b}
\end{eqnarray}\)
③ 点 \(\rm E\) は直線 \(\rm AB\) 上の点でもあるので、係数の和が \(1\) となることより、\(k\) の値を求める。
点 \({\rm E}\) が直線 \({\rm AB}\) 上にあるとき、
\(\overrightarrow{\rm OE}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}~,~s+t=1\)
\(\begin{eqnarray}~~~\displaystyle \frac{\,2\,}{\,5\,}k+\displaystyle \frac{\,1\,}{\,5\,}k=1~\Leftrightarrow ~ k=\displaystyle \frac{\,5\,}{\,3\,}
\end{eqnarray}\)
④ 比の値を求める。
\(\overrightarrow{\rm OE}=\displaystyle \frac{\,5\,}{\,3\,}\,\overrightarrow{\rm OP}\) より、\(\rm OP:PE=3:2\)
\(\overrightarrow{\rm OE}=\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{b}\) より、
内分の式となり、\(\rm AE:EB=1:2\)
\(\triangle {\rm OAB}\) の内部点 \(\rm P\) において、\(\rm OP\) の延長と \(\rm AB\) の交点を \(\rm E\) としたとき、
① \(\overrightarrow{\rm OP}\) を位置ベクトル \(\overrightarrow{a}\) と \(\overrightarrow{b}\) を用いて表す。
\(\overrightarrow{\rm OP}=\displaystyle \frac{\,2\,}{\,5\,}\overrightarrow{a}
+\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{b}\)
※ 求め方は、こちらを参照してください。
② 点 \(\rm E\) は直線 \({\rm OP}\) の延長線上より、\(\overrightarrow{\rm OE}=k\,\overrightarrow{\rm OP}\) となる。
\(\begin{eqnarray}~~~\overrightarrow{\rm OE}&=&k\,\overrightarrow{\rm OP}=\displaystyle \frac{\,2\,}{\,5\,}k\,\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,5\,}k\,\overrightarrow{b}
\end{eqnarray}\)
③ 点 \(\rm E\) は直線 \(\rm AB\) 上の点でもあるので、係数の和が \(1\) となることより、\(k\) の値を求める。
点 \({\rm E}\) が直線 \({\rm AB}\) 上にあるとき、
\(\overrightarrow{\rm OE}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}~,~s+t=1\)
\(\begin{eqnarray}~~~\displaystyle \frac{\,2\,}{\,5\,}k+\displaystyle \frac{\,1\,}{\,5\,}k=1~\Leftrightarrow ~ k=\displaystyle \frac{\,5\,}{\,3\,}
\end{eqnarray}\)
④ 比の値を求める。
\(\overrightarrow{\rm OE}=\displaystyle \frac{\,5\,}{\,3\,}\,\overrightarrow{\rm OP}\) より、\(\rm OP:PE=3:2\)
\(\overrightarrow{\rm OE}=\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{b}\) より、
内分の式となり、\(\rm AE:EB=1:2\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
三角形の線分の比と面積比
Point:三角形の線分の比と面積比三角形の線分の比から面積比の求め方は、
■ 高さが等しいとき、

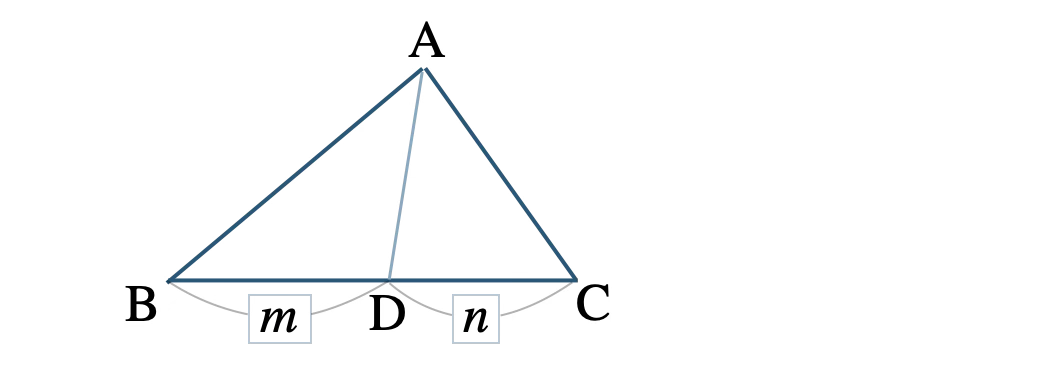
底辺の比が \(m:n\) のとき、
面積比は、
\(\triangle {\rm ABD}:\triangle {\rm ADC}=m:n\)

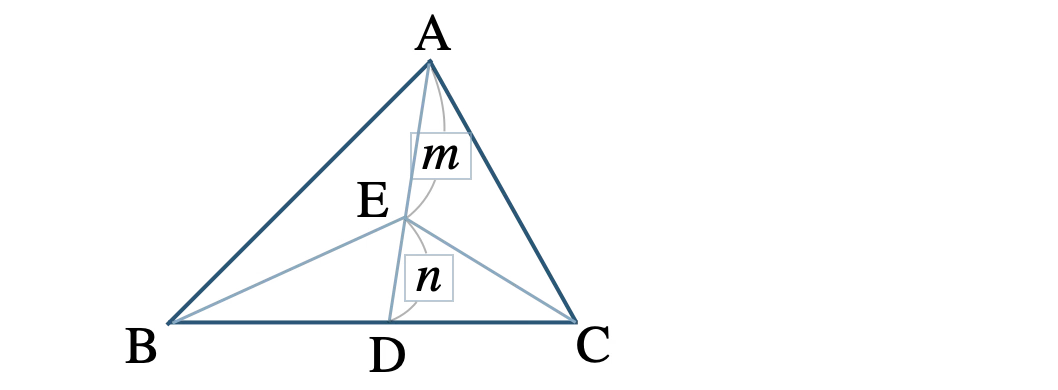
\({\rm AE:ED}=m:n\) のとき、
面積比は、
\(\triangle {\rm ABC}:\triangle {\rm EBC}=m+n:n\)
■ 高さが等しいとき、


底辺の比が \(m:n\) のとき、
面積比は、
\(\triangle {\rm ABD}:\triangle {\rm ADC}=m:n\)
■ 底辺が等しいとき、
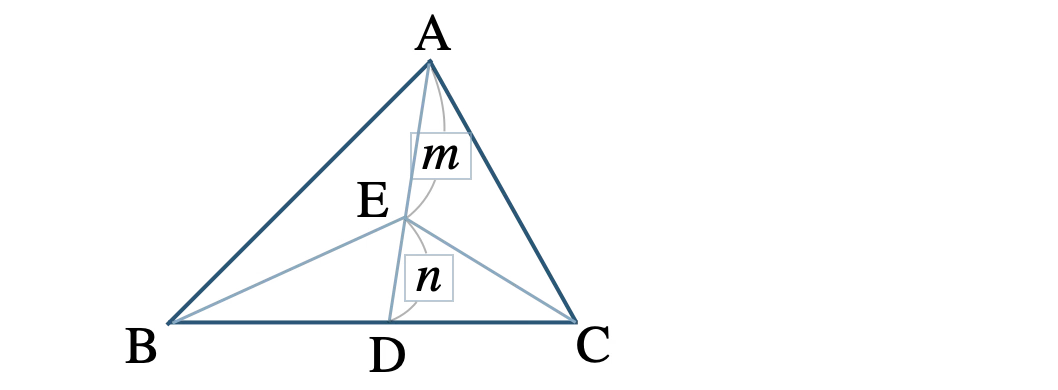
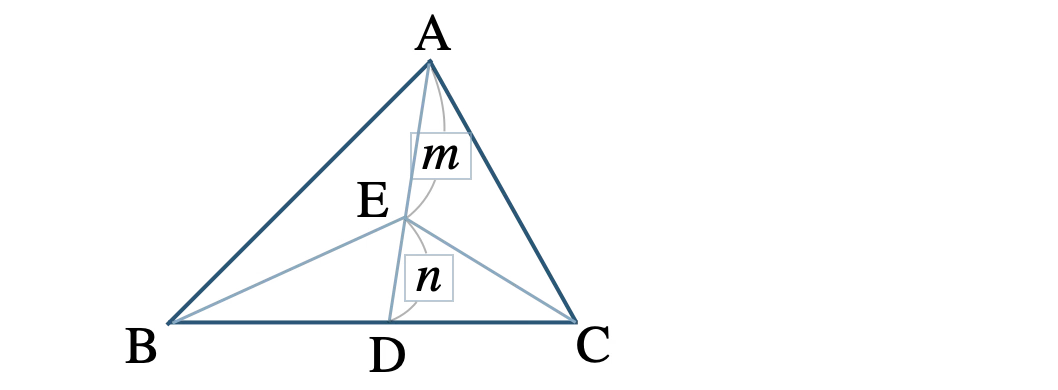
\({\rm AE:ED}=m:n\) のとき、
面積比は、
\(\triangle {\rm ABC}:\triangle {\rm EBC}=m+n:n\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|三角形の内部の点と線分の比・面積比
平面上のベクトル 61☆\(\triangle {\rm OAB}\) ( \(\overrightarrow{\rm OA}=\overrightarrow{a}~,~ \overrightarrow{\rm OB}=\overrightarrow{b}\) ) において、辺 \({\rm OA}\) の中点を \(\rm C\)、辺 \({\rm OB}\) を \(1:2\) に内分する点を \(\rm D\) 、2直線 \(\rm AD\) と \(\rm BC\) の交点 \(\rm P\)、直線 \(\rm OP\) と辺 \(\rm AB\) が交わる点を \(\rm E\) とするとき、\(\rm OP:PE\) と \(\rm AE:EB\) の求め方は?また、\(\triangle {\rm OAB}~,~\triangle {\rm PAB}~,~\triangle {\rm OAP}~,~\triangle {\rm PEB}\) の面積比の求め方は?
高校数学C|平面上のベクトル
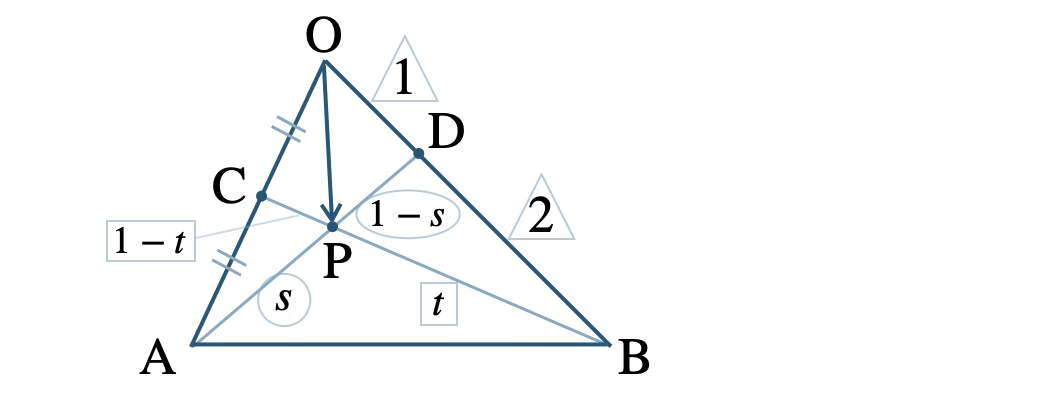
\({\rm AP:PD}=s:1-s \) とおくと、
\(\triangle { \rm OAD }\) において、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&(1-s)\cdot\overrightarrow{\rm OA}+s\cdot\overrightarrow{\rm OD}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm OD}=\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{\rm OB}=\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{b}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&(1-s)\,\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}s\,\overrightarrow{b}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
次に \({\rm BP:PC}=t:1-t\) とおくと、
\(\triangle { \rm OCB }\) において、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&t\cdot\overrightarrow{\rm OC}+(1-t)\cdot\overrightarrow{\rm OB}
\end{eqnarray}\)
ここで、\(\overrightarrow{\rm OC}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OA}
=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&\displaystyle \frac{\,1\,}{\,2\,}t\,\overrightarrow{a}+(1-t)\,\overrightarrow{b}~ ~ ~ \cdots {\small [\,2\,]}\end{eqnarray}\)
\({\small [\,1\,]}~,~{\small [\,2\,]}\) より、
\(\overrightarrow{a}\neq \overrightarrow{0}~,~\overrightarrow{b}\neq \overrightarrow{0}\) かつ \(\overrightarrow{a}\) と \(\overrightarrow{b}\) が平行でないので、係数を比較すると、
\(\begin{eqnarray}~~~1-s&=&\displaystyle \frac{\,1\,}{\,2\,}t~ ~ ~ ~\,\cdots {\small [\,3\,]}
\\[5pt]~~~\displaystyle \frac{\,1\,}{\,3\,}s&=&1-t~ ~ ~ \cdots {\small [\,4\,]}
\end{eqnarray}\)
\({\small [\,3\,]}\) より \(t=2-2s\) を \({\small [\,4\,]}\) に代入すると、
\(\begin{eqnarray}~~~\displaystyle \frac{\,1\,}{\,3\,}s&=&1-(2-2s)
\\[5pt]~~~\displaystyle \frac{\,1\,}{\,3\,}s&=&-1+2s
\\[5pt]~~~s&=&-3+6s
\\[5pt]~~~-5s&=&-3
\\[5pt]~~~s&=&\displaystyle \frac{\,3\,}{\,5\,}
\end{eqnarray}\)
\({\small [\,1\,]}\) に代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&\left(1-\displaystyle \frac{\,3\,}{\,5\,}\right)\overrightarrow{a}
+\displaystyle \frac{\,1\,}{\,3\,}\cdot\displaystyle \frac{\,3\,}{\,5\,}\cdot\overrightarrow{b}
\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,5\,}\overrightarrow{a}
+\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{b}~ ~ ~ \cdots {\small [\,5\,]}
\end{eqnarray}\)
ここで、点 \(\rm E\) は直線 \(\rm OP\) の延長線上にあるので、\(\overrightarrow{\rm OE}=k\,\overrightarrow{\rm OP}\) となり、
\(\begin{eqnarray}~~~\overrightarrow{\rm OE}&=&k\,\overrightarrow{\rm OP}
\\[5pt]~~~&=&k\left(\displaystyle \frac{\,2\,}{\,5\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{b}\right)\hspace{30pt}(\,∵~ {\small [\,5\,]}\,)
\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,5\,}k\,\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,5\,}k\,\overrightarrow{b}~ ~ ~ \cdots {\small [\,6\,]}
\end{eqnarray}\)
また、\(\rm E\) は辺 \(\rm AB\) 上にあり、係数の和が \(1\) となるので、
\(\begin{eqnarray}~~~\displaystyle \frac{\,2\,}{\,5\,}k+\displaystyle \frac{\,1\,}{\,5\,}k&=&1
\\[5pt]~~~\displaystyle \frac{\,3\,}{\,5\,}k&=&1
\\[5pt]~~~k&=&\displaystyle \frac{\,5\,}{\,3\,}
\end{eqnarray}\)
よって、\(\overrightarrow{\rm OE}=\displaystyle \frac{\,5\,}{\,3\,}\overrightarrow{\rm OP}\) となる
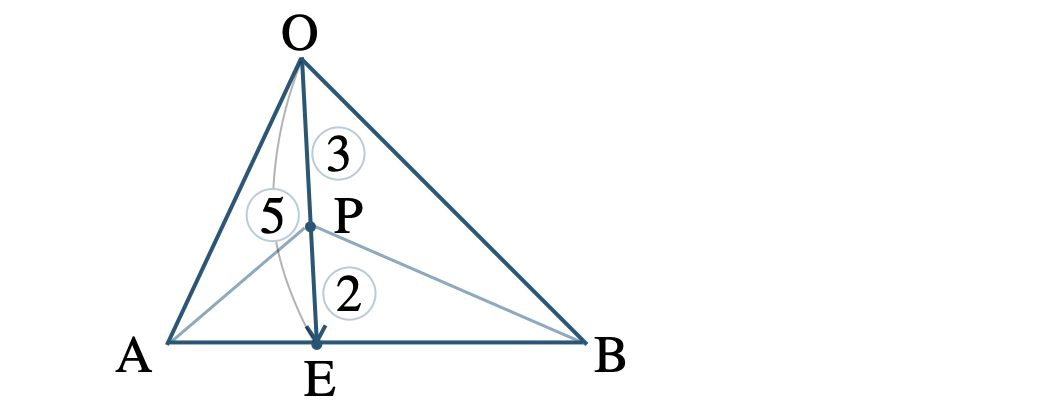

これより、\(\rm OP:OE=3:5\) となるので、
\(\rm OP:PE=3:2\) となる
次に、\({\small [\,6\,]}\) に \(k=\displaystyle \frac{\,5\,}{\,3\,}\) を代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OE}&=&\displaystyle \frac{\,2\,}{\,5\,}{\, \small \times \,}\displaystyle \frac{\,5\,}{\,3\,}\,\overrightarrow{a}
+\displaystyle \frac{\,1\,}{\,5\,}{\, \small \times \,}\displaystyle \frac{\,5\,}{\,3\,}\,\overrightarrow{b}
\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{b}
\\[5pt]~~~&=&\displaystyle \frac{\,2\overrightarrow{a}+\overrightarrow{b}\,}{\,1+2\,}
\end{eqnarray}\)
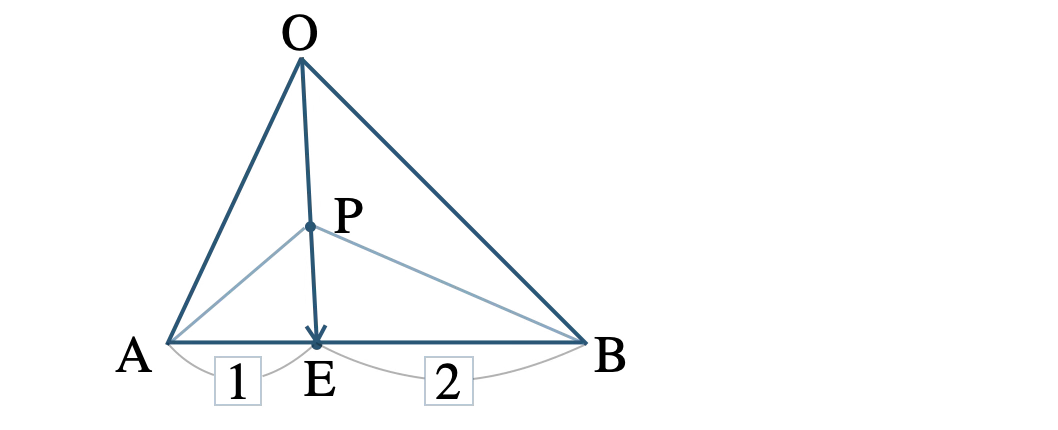

内分の式より、\(\rm AE:EB=1:2\) となる
\(\triangle {\rm OAB}\) の面積を基準にすると、
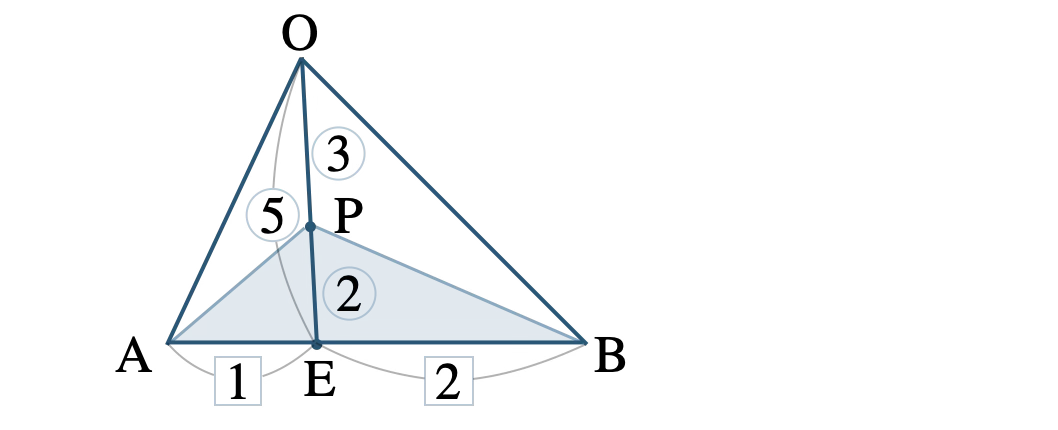

\(\triangle {\rm PAB}\) は底辺が等しく、\(\rm OE:PE=5:2\) より、
\(\triangle {\rm PAB}=\displaystyle \frac{\,2\,}{\,5\,}\triangle {\rm OAB}~ ~ ~ \cdots {\small [\,7\,]}\)
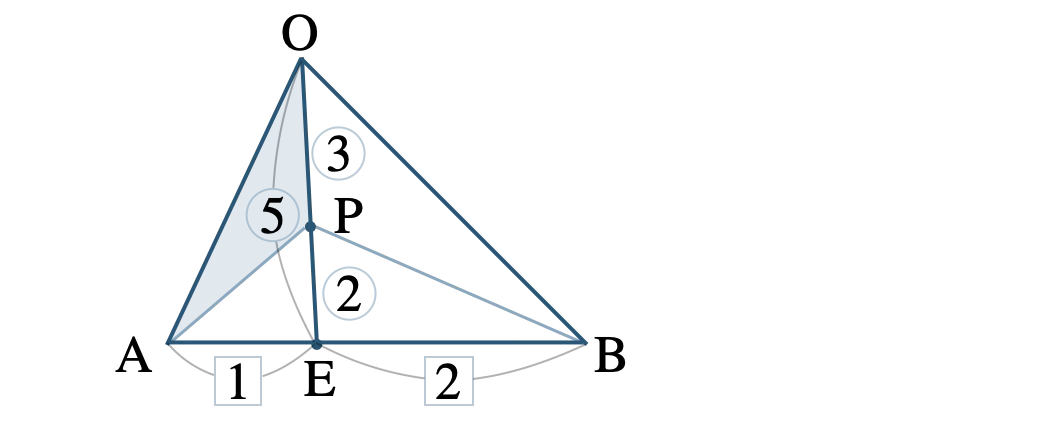
次に、\(\triangle {\rm OAE}\) は、\(\rm AE:EB=1:2\) より、
\(\triangle {\rm OAE}=\displaystyle \frac{\,1\,}{\,3\,}\triangle {\rm OAB}\)
さらに、\(\triangle {\rm OAP}\) は底辺が等しく、\(\rm OE:OP=5:3\) より、
\(\begin{eqnarray}~~~\triangle {\rm OAP}&=&\displaystyle \frac{\,3\,}{\,5\,}\,\triangle {\rm OAE}
\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,5\,}{\, \small \times \,}\displaystyle \frac{\,1\,}{\,3\,}\triangle {\rm OAB}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,5\,}\triangle {\rm OAB}~ ~ ~ \cdots {\small [\,8\,]}
\end{eqnarray}\)
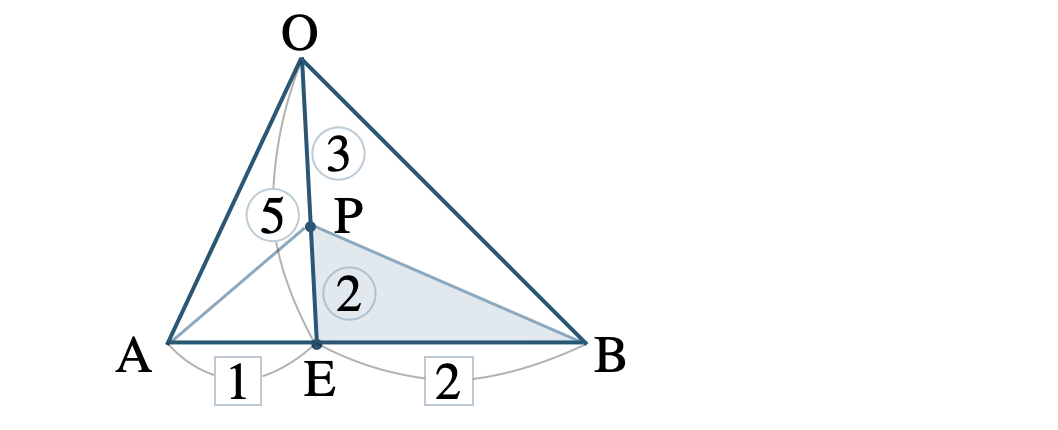
次に、\(\triangle {\rm OEB}\) は、\(\rm AE:EB=1:2\) より、
\(\triangle {\rm OEB}=\displaystyle \frac{\,2\,}{\,3\,}\triangle {\rm OAB}\)
さらに、\(\triangle {\rm PEB}\) は底辺が等しく、\(\rm OE:PE=5:2\) より、
\(\begin{eqnarray}~~~\triangle {\rm PEB}&=&\displaystyle \frac{\,2\,}{\,5\,}\,\triangle {\rm OEB}
\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,5\,}{\, \small \times \,}\displaystyle \frac{\,2\,}{\,3\,}\triangle {\rm OAB}
\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,15\,}\triangle {\rm OAB}~ ~ ~ \cdots {\small [\,9\,]}
\end{eqnarray}\)
\(\small [\,7\,]\)〜\(\small [\,9\,]\) より、\(\triangle {\rm OAB}\) の面積を \(1\) とした面積比は、
\(\begin{eqnarray}~~~&&\triangle {\rm OAB}:\triangle {\rm PAB}:\triangle {\rm OAP}:\triangle {\rm PEB}
\\[5pt]~~~&=&1\,:\,\displaystyle \frac{\,2\,}{\,5\,}\,:\,\displaystyle \frac{\,1\,}{\,5\,}\,:\,\displaystyle \frac{\,4\,}{\,15\,}
\\[5pt]~~~&=&1{\, \small \times \,}15\,:\,\displaystyle \frac{\,2\,}{\,5\,}{\, \small \times \,}15\,:\,\displaystyle \frac{\,1\,}{\,5\,}{\, \small \times \,}15\,:\,\displaystyle \frac{\,4\,}{\,15\,}{\, \small \times \,}15
\\[5pt]~~~&=&15\,:\,6\,:\,3\,:\,4
\end{eqnarray}\)




