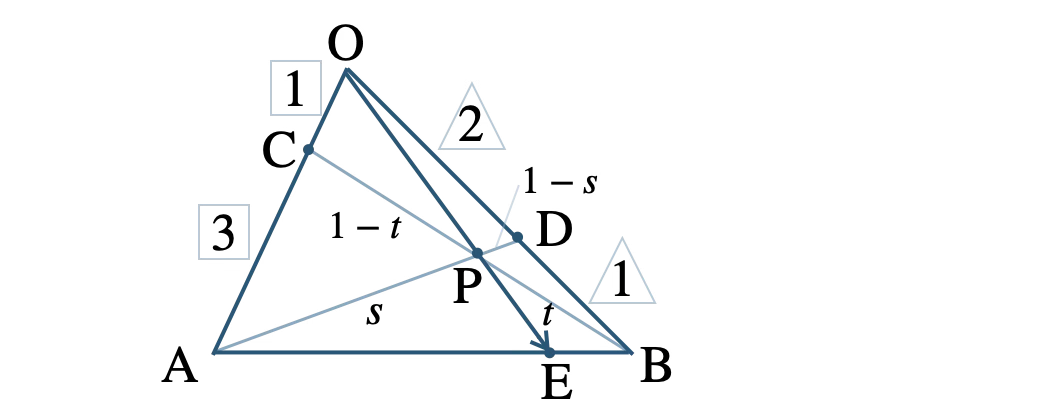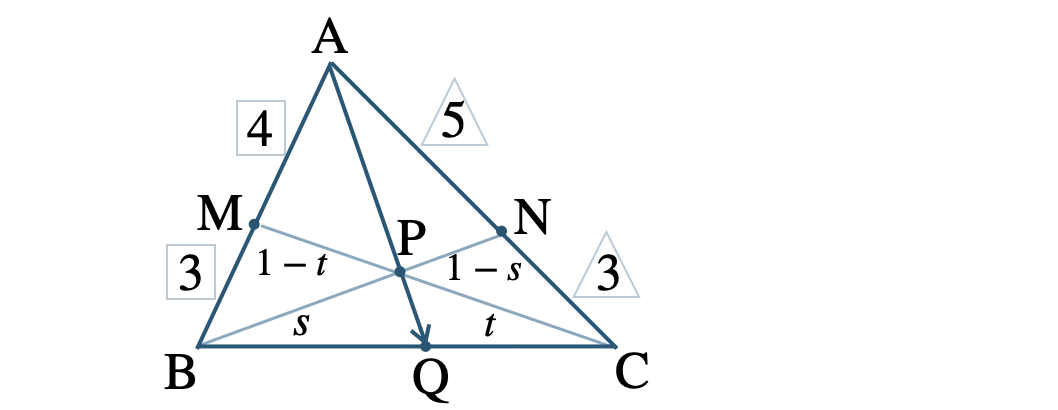このページは、「三角形の内部の点と線分の比・面積比」の練習問題アーカイブページとなります。
この問題の解き方の詳細は↓
三角形の内部の点と線分の比・面積比 で確認できます。
問題アーカイブ01
問題アーカイブ01\(\triangle {\rm OAB}\) において、辺 \({\rm OA}\) を \(1:3\) 、辺 \({\rm OB}\) を \(2:1\) に内分する点を、それぞれ \(\rm C\) 、\(\rm D\) とし、また、2線分 \(\rm AD\) 、\(\rm BC\) の交点を \(\rm P\) 、線分 \(\rm OP\) の延長が辺 \(\rm AB\) と交わる点を \(\rm E\) とする。\(\overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}\) とするとき、ベクトル \(\overrightarrow{\rm OE}\) を \(\overrightarrow{a}~,~\overrightarrow{b}\) を用いて表せ。また、\(\rm AE:EB\) を求めよ。
数研出版|数学C[708] p.47 問題 10
\({\rm AP:PD}=s:1-s \) とおくと、
\(\triangle { \rm OAD }\) において、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&(1-s)\cdot\overrightarrow{\rm OA}+s\cdot\overrightarrow{\rm OD}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm OD}=\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{\rm OB}=\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&(1-s)\,\overrightarrow{a}+\displaystyle \frac{\,2\,}{\,3\,}s\,\overrightarrow{b}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
次に \({\rm BP:PC}=t:1-t\) とおくと、
\(\triangle { \rm OCB }\) において、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&t\cdot\overrightarrow{\rm OC}+(1-t)\cdot\overrightarrow{\rm OB}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm OC}=\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{\rm OA}=\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{a}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&\displaystyle \frac{\,1\,}{\,4\,}t\,\overrightarrow{a}+(1-t)\,\overrightarrow{b}~ ~ ~ \cdots {\small [\,2\,]}\end{eqnarray}\)
\({\small [\,1\,]}~,~{\small [\,2\,]}\) より、
\(\overrightarrow{a}\neq \overrightarrow{0}~,~\overrightarrow{b}\neq \overrightarrow{0}\) かつ \(\overrightarrow{a}\) と \(\overrightarrow{b}\) が平行でないので、係数を比較すると、
\(\begin{eqnarray}~~~1-s&=&\displaystyle \frac{\,1\,}{\,4\,}t~ ~ ~ ~\,\cdots {\small [\,3\,]}\\[5pt]~~~\displaystyle \frac{\,2\,}{\,3\,}s&=&1-t~ ~ ~ \cdots {\small [\,4\,]}\end{eqnarray}\)
\({\small [\,3\,]}\) より \(t=4-4s\) を \({\small [\,4\,]}\) に代入すると、
\(\begin{eqnarray}~~~\displaystyle \frac{\,2\,}{\,3\,}s&=&1-(4-4s)\\[5pt]~~~\displaystyle \frac{\,2\,}{\,3\,}s&=&-3+4s\\[5pt]~~~2s&=&-9+12s\\[5pt]~~~-10s&=&-9\\[5pt]~~~s&=&\displaystyle \frac{\,9\,}{\,10\,}\end{eqnarray}\)
\({\small [\,1\,]}\) に代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&\left(1-\displaystyle \frac{\,9\,}{\,10\,}\right)\overrightarrow{a}+\displaystyle \frac{\,2\,}{\,3\,}\cdot\displaystyle \frac{\,9\,}{\,10\,}\cdot\overrightarrow{b}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,10\,}\overrightarrow{a}+\displaystyle \frac{\,3\,}{\,5\,}\overrightarrow{b}~ ~ ~ \cdots {\small [\,5\,]}\end{eqnarray}\)
ここで、点 \(\rm E\) は直線 \(\rm OP\) の延長線上にあるので、\(\overrightarrow{\rm OE}=k\,\overrightarrow{\rm OP}\) となり、
\(\begin{eqnarray}~~~\overrightarrow{\rm OE}&=&k\,\overrightarrow{\rm OP}\\[5pt]~~~&=&k\left(\displaystyle \frac{\,1\,}{\,10\,}\overrightarrow{a}+\displaystyle \frac{\,3\,}{\,5\,}\overrightarrow{b}\right)\hspace{30pt}(\,∵~ {\small [\,5\,]}\,)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,10\,}k\,\overrightarrow{a}+\displaystyle \frac{\,3\,}{\,5\,}k\,\overrightarrow{b}~ ~ ~ \cdots {\small [\,6\,]}\end{eqnarray}\)
また、\(\rm E\) は辺 \(\rm AB\) 上にあり、係数の和が \(1\) となるので、
\(\begin{eqnarray}~~~\displaystyle \frac{\,1\,}{\,10\,}k+\displaystyle \frac{\,3\,}{\,5\,}k&=&1\\[5pt]~~~\displaystyle \frac{\,7\,}{\,10\,}k&=&1\\[5pt]~~~k&=&\displaystyle \frac{\,10\,}{\,7\,}\end{eqnarray}\)
次に、\({\small [\,6\,]}\) に \(k=\displaystyle \frac{\,10\,}{\,7\,}\) を代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OE}&=&\displaystyle \frac{\,1\,}{\,10\,}{\, \small \times \,}\displaystyle \frac{\,10\,}{\,7\,}\,\overrightarrow{a}+\displaystyle \frac{\,3\,}{\,5\,}{\, \small \times \,}\displaystyle \frac{\,10\,}{\,7\,}\,\overrightarrow{b}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,7\,}\overrightarrow{a}+\displaystyle \frac{\,6\,}{\,7\,}\overrightarrow{b}\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{a}+6\overrightarrow{b}\,}{\,1+6\,}\end{eqnarray}\)
内分の式より、\(\rm AE:EB=6:1\) となる
問題アーカイブ02
問題アーカイブ02平行四辺形 \({\rm OABC}\) において、辺 \({\rm OA}\) の中点を \(\rm D\) 、辺 \({\rm OC}\) を \(2:1\) に内分する点を \(\rm E\) とし、線分 \({\rm DE}\) を \(1:3\) に内分する点を \(\rm P\) 、直線 \({\rm OP}\) と直線 \({\rm AB}\) の交点を \(\rm F\) とする。
\({\small (1)}~\)\(\overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OC}=\overrightarrow{c}\) とするとき、\(\overrightarrow{\rm OF}\) を \(\overrightarrow{a}~,~\overrightarrow{c}\) を用いて表せ。
\({\small (2)}~\)四角形 \({\rm OAFE}\) の面積は平行四辺形 \({\rm OABC}\) の面積の何倍であるか。
\({\small (1)}~\)\(\overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OC}=\overrightarrow{c}\) とするとき、\(\overrightarrow{\rm OF}\) を \(\overrightarrow{a}~,~\overrightarrow{c}\) を用いて表せ。
\({\small (2)}~\)四角形 \({\rm OAFE}\) の面積は平行四辺形 \({\rm OABC}\) の面積の何倍であるか。
数研出版|数学C[708] p.48 演習問題A 2
\({\small (1)}~\)点 \(\rm D\) は辺 \({\rm OA}\) の中点、点 \(\rm E\) は辺 \({\rm OC}\) を \(2:1\) に内分する点より、

\(\begin{eqnarray}~~~\overrightarrow{\rm OD}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}\\[5pt]~~~\overrightarrow{\rm OE}&=&\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{c}\end{eqnarray}\)
点 \(\rm P\) は線分 \({\rm DE}\) を \(1:3\) に内分する点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&\displaystyle \frac{\,3\cdot\overrightarrow{\rm OD}+1\cdot\overrightarrow{\rm OE}\,}{\,1+3\,}\\[5pt]~~~&=&\displaystyle \frac{\,3\cdot\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{c}\,}{\,4\,}\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,8\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,6\,}\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
ここで、点 \(\rm F\) は直線 \(\rm OP\) 上にあるので、\(\overrightarrow{\rm OF}=k\,\overrightarrow{\rm OP}\) となり、
\(\begin{eqnarray}~~~\overrightarrow{\rm OF}&=&k\,\overrightarrow{\rm OP}\\[5pt]~~~&=&k\left(\displaystyle \frac{\,3\,}{\,8\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,6\,}\overrightarrow{c}\right)\hspace{30pt}(\,∵~ {\small [\,1\,]}\,)\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,8\,}k\,\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,6\,}k\,\overrightarrow{c}~ ~ ~ \cdots {\small [\,2\,]}\end{eqnarray}\)
また、点 \(\rm F\) は直線 \(\rm AB\) 上にあるので、
平行四辺形より \(\overrightarrow{\rm AB}=\overrightarrow{\rm OC}=\overrightarrow{c}\) となり、
\(\begin{eqnarray}~~~\overrightarrow{\rm OF}&=&\overrightarrow{\rm OA}+t\,\overrightarrow{\rm AB}\\[5pt]~~~&=&\overrightarrow{a}+t\,\overrightarrow{c}~ ~ ~ \cdots {\small [\,3\,]}\end{eqnarray}\)
\({\small [\,2\,]}~,~{\small [\,3\,]}\) より、
\(\overrightarrow{a}\neq \overrightarrow{0}~,~\overrightarrow{c}\neq \overrightarrow{0}\) かつ \(\overrightarrow{a}\) と \(\overrightarrow{c}\) が平行でないので、係数を比較すると、
\(\begin{eqnarray}~~~\displaystyle \frac{\,3\,}{\,8\,}k&=&1~ ~ ~ ~\,\cdots {\small [\,4\,]}\\[5pt]~~~\displaystyle \frac{\,1\,}{\,6\,}k&=&t~ ~ ~ \cdots {\small [\,5\,]}\end{eqnarray}\)
\({\small [\,4\,]}\) より、
\(\begin{eqnarray}~~~k&=&\displaystyle \frac{\,8\,}{\,3\,}\end{eqnarray}\)
\({\small [\,2\,]}\) に代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OF}&=&\displaystyle \frac{\,3\,}{\,8\,}{\, \small \times \,}\displaystyle \frac{\,8\,}{\,3\,}\,\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,6\,}{\, \small \times \,}\displaystyle \frac{\,8\,}{\,3\,}\,\overrightarrow{c}\\[5pt]~~~&=&\overrightarrow{a}+\displaystyle \frac{\,4\,}{\,9\,}\overrightarrow{c}\end{eqnarray}\)
\({\small (2)}~\)平行四辺形 \({\rm OABC}\) の面積を \(S\) とすると、
\(\triangle {\rm OAF}\) は、\({\rm AF}=\displaystyle \frac{\,4\,}{\,9\,}{\rm AB}=\displaystyle \frac{\,4\,}{\,9\,}{\rm OC}\) より、
\(\begin{eqnarray}~~~\triangle {\rm OAF}&=&\displaystyle \frac{\,4\,}{\,9\,}\triangle {\rm OAB}\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,9\,}{\, \small \times \,}\displaystyle \frac{\,1\,}{\,2\,}S\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,9\,}S~ ~ ~ \cdots {\small [\,6\,]}\end{eqnarray}\)
次に、\(\triangle {\rm OEF}\) は、\({\rm OE}=\displaystyle \frac{\,2\,}{\,3\,}{\rm OC}\) より、
\(\begin{eqnarray}~~~\triangle {\rm OEF}&=&\displaystyle \frac{\,2\,}{\,3\,}\triangle {\rm OCF}\end{eqnarray}\)
ここで、\(\triangle {\rm OCF}\) は、\({\rm CF}={\rm AB}-{\rm AF}={\rm OC}-\displaystyle \frac{\,4\,}{\,9\,}{\rm OC}=\displaystyle \frac{\,5\,}{\,9\,}{\rm OC}\) より、
\(\begin{eqnarray}~~~\triangle {\rm OCF}&=&\displaystyle \frac{\,5\,}{\,9\,}\triangle {\rm OCA}\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,9\,}{\, \small \times \,}\displaystyle \frac{\,1\,}{\,2\,}S\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,18\,}S\end{eqnarray}\)
よって、
\(\begin{eqnarray}~~~\triangle {\rm OEF}&=&\displaystyle \frac{\,2\,}{\,3\,}{\, \small \times \,}\displaystyle \frac{\,5\,}{\,18\,}S\\[5pt]~~~&=&\displaystyle \frac{\,5\,}{\,27\,}S~ ~ ~ \cdots {\small [\,7\,]}\end{eqnarray}\)
\({\small [\,6\,]}~,~{\small [\,7\,]}\) より、四角形 \({\rm OAFE}\) の面積は、
\(\begin{eqnarray}~~~四角形{\rm OAFE}&=&\triangle {\rm OAF}+\triangle {\rm OEF}\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,9\,}S+\displaystyle \frac{\,5\,}{\,27\,}S\\[5pt]~~~&=&\displaystyle \frac{\,6\,}{\,27\,}S+\displaystyle \frac{\,5\,}{\,27\,}S\\[5pt]~~~&=&\displaystyle \frac{\,11\,}{\,27\,}S\end{eqnarray}\)
したがって、四角形 \({\rm OAFE}\) の面積は平行四辺形 \({\rm OABC}\) の面積の \(\displaystyle \frac{\,11\,}{\,27\,}\) 倍となる
問題アーカイブ03
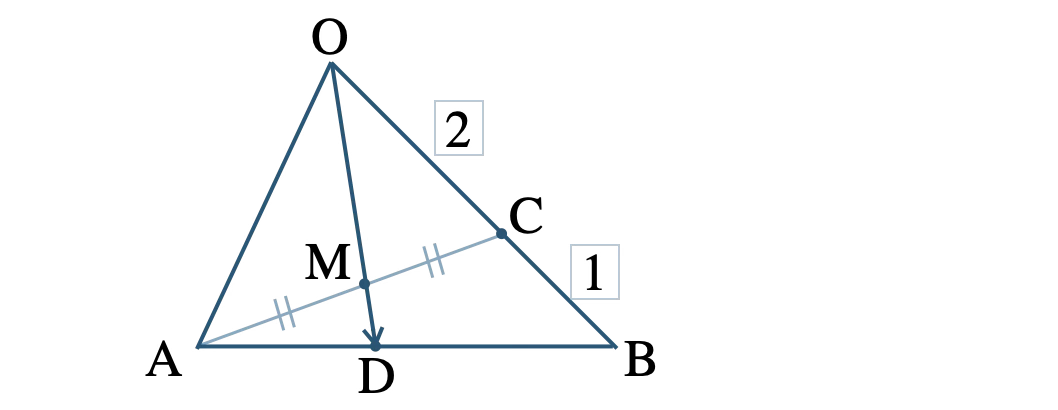
問題アーカイブ03\(\triangle {\rm OAB}\) において、辺 \({\rm OB}\) を \(2:1\) に内分する点を \(\rm C\) 、線分 \({\rm AC}\) の中点を \(\rm M\) とし、直線 \({\rm OM}\) と辺 \({\rm AB}\) の交点を \(\rm D\) とする。次のものを求めよ。
\({\small (1)}~\)\(\overrightarrow{\rm OD}=k\,\overrightarrow{\rm OM}\) となる実数 \(k\) の値
\({\small (2)}~\)\({\rm AD:DB}\)
\({\small (1)}~\)\(\overrightarrow{\rm OD}=k\,\overrightarrow{\rm OM}\) となる実数 \(k\) の値
\({\small (2)}~\)\({\rm AD:DB}\)
数研出版|高等学校数学C[709] p.48 章末問題B 9
数研出版|新編数学C[710] p.49 章末問題B 8
\(\overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}\) とおくと、
点 \(\rm C\) は辺 \({\rm OB}\) を \(2:1\) に内分する点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OC}&=&\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}\end{eqnarray}\)
点 \(\rm M\) は線分 \({\rm AC}\) の中点より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,\overrightarrow{\rm OA}+\overrightarrow{\rm OC}\,}{\,2\,}\\[5pt]~~~&=&\displaystyle \frac{\,\overrightarrow{a}+\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}\,}{\,2\,}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{b}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
ここで、点 \(\rm D\) は直線 \(\rm OM\) 上にあるので、\(\overrightarrow{\rm OD}=k\,\overrightarrow{\rm OM}\) となり、
\(\begin{eqnarray}~~~\overrightarrow{\rm OD}&=&k\,\overrightarrow{\rm OM}\\[5pt]~~~&=&k\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{b}\right)\hspace{30pt}(\,∵~ {\small [\,1\,]}\,)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}k\,\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}k\,\overrightarrow{b}~ ~ ~ \cdots {\small [\,2\,]}\end{eqnarray}\)
また、\(\rm D\) は辺 \(\rm AB\) 上にあり、係数の和が \(1\) となるので、
\(\begin{eqnarray}~~~\displaystyle \frac{\,1\,}{\,2\,}k+\displaystyle \frac{\,1\,}{\,3\,}k&=&1\\[5pt]~~~\displaystyle \frac{\,5\,}{\,6\,}k&=&1\\[5pt]~~~k&=&\displaystyle \frac{\,6\,}{\,5\,}\end{eqnarray}\)
\({\small (1)}~\)したがって、\(k=\displaystyle \frac{\,6\,}{\,5\,}\)
\({\small (2)}~\)\({\small [\,2\,]}\) に \(k=\displaystyle \frac{\,6\,}{\,5\,}\) を代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OD}&=&\displaystyle \frac{\,1\,}{\,2\,}{\, \small \times \,}\displaystyle \frac{\,6\,}{\,5\,}\,\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}{\, \small \times \,}\displaystyle \frac{\,6\,}{\,5\,}\,\overrightarrow{b}\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,5\,}\overrightarrow{a}+\displaystyle \frac{\,2\,}{\,5\,}\overrightarrow{b}\\[5pt]~~~&=&\displaystyle \frac{\,3\overrightarrow{a}+2\overrightarrow{b}\,}{\,3+2\,}\end{eqnarray}\)
内分の式より、\(\rm AD:DB=2:3\) となる
問題アーカイブ04
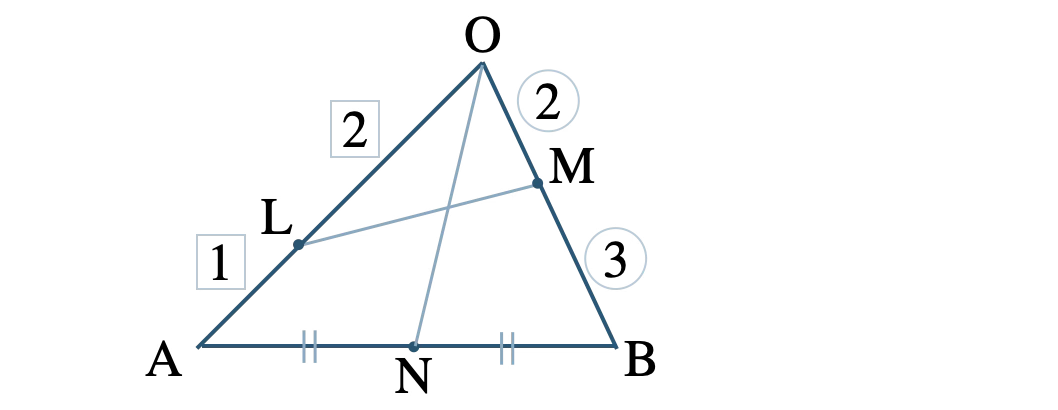
問題アーカイブ04\(\triangle {\rm OAB}\) において、辺 \({\rm OA}\) を \(2:1\) に内分する点を \(\rm L\) 、辺 \({\rm OB}\) を \(2:3\) に内分する点を \(\rm M\) 、辺 \({\rm AB}\) の中点を \(\rm N\) とする。線分 \({\rm LM}\) と線分 \({\rm ON}\) との交点を \(\rm P\) とするとき、\(\overrightarrow{\rm OP}\) を \(\overrightarrow{\rm OA}=\overrightarrow{a}\) と \(\overrightarrow{\rm OB}=\overrightarrow{b}\) で表せ。また、\({\rm LP:PM}\) 、\({\rm OP:PN}\) を求めよ。
東京書籍|Advanced数学C[701] p.44 問題 9
\({\rm LP:PM}=s:1-s \) とおくと、
\(\triangle { \rm OLM }\) において、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&(1-s)\cdot\overrightarrow{\rm OL}+s\cdot\overrightarrow{\rm OM}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm OL}=\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{\rm OA}=\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{a}~,~\overrightarrow{\rm OM}=\displaystyle \frac{\,2\,}{\,5\,}\overrightarrow{\rm OB}=\displaystyle \frac{\,2\,}{\,5\,}\overrightarrow{b}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&\displaystyle \frac{\,2\,}{\,3\,}(1-s)\,\overrightarrow{a}+\displaystyle \frac{\,2\,}{\,5\,}s\,\overrightarrow{b}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
次に \({\rm OP:PN}=t:1-t\) とおくと、
\(\overrightarrow{\rm ON}=\displaystyle \frac{\,\overrightarrow{\rm OA}+\overrightarrow{\rm OB}\,}{\,2\,}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&t\cdot\overrightarrow{\rm ON}\\[5pt]~~~&=&t\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}t\,\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}t\,\overrightarrow{b}~ ~ ~ \cdots {\small [\,2\,]}\end{eqnarray}\)
\({\small [\,1\,]}~,~{\small [\,2\,]}\) より、
\(\overrightarrow{a}\neq \overrightarrow{0}~,~\overrightarrow{b}\neq \overrightarrow{0}\) かつ \(\overrightarrow{a}\) と \(\overrightarrow{b}\) が平行でないので、係数を比較すると、
\(\begin{eqnarray}~~~\displaystyle \frac{\,2\,}{\,3\,}(1-s)&=&\displaystyle \frac{\,1\,}{\,2\,}t~ ~ ~ ~\,\cdots {\small [\,3\,]}\\[5pt]~~~\displaystyle \frac{\,2\,}{\,5\,}s&=&\displaystyle \frac{\,1\,}{\,2\,}t~ ~ ~ \cdots {\small [\,4\,]}\end{eqnarray}\)
\({\small [\,3\,]}\) より \(t=\displaystyle \frac{\,4\,}{\,3\,}(1-s)\) を \({\small [\,4\,]}\) に代入すると、
\(\begin{eqnarray}~~~\displaystyle \frac{\,2\,}{\,5\,}s&=&\displaystyle \frac{\,1\,}{\,2\,}{\, \small \times \,}\displaystyle \frac{\,4\,}{\,3\,}(1-s)\\[5pt]~~~\displaystyle \frac{\,2\,}{\,5\,}s&=&\displaystyle \frac{\,2\,}{\,3\,}(1-s)\\[5pt]~~~\displaystyle \frac{\,s\,}{\,5\,}&=&\displaystyle \frac{\,1-s\,}{\,3\,}\\[5pt]~~~3s&=&5(1-s)\\[5pt]~~~3s&=&5-5s\\[5pt]~~~8s&=&5\\[5pt]~~~s&=&\displaystyle \frac{\,5\,}{\,8\,}\end{eqnarray}\)
\({\small [\,4\,]}\) より、
\(\begin{eqnarray}~~~t&=&\displaystyle \frac{\,2\,}{\,5\,}s{\, \small \times \,}2\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,5\,}{\, \small \times \,}\displaystyle \frac{\,5\,}{\,8\,}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\end{eqnarray}\)
\({\small [\,1\,]}\) に代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&\displaystyle \frac{\,2\,}{\,3\,}\left(1-\displaystyle \frac{\,5\,}{\,8\,}\right)\overrightarrow{a}+\displaystyle \frac{\,2\,}{\,5\,}{\, \small \times \,}\displaystyle \frac{\,5\,}{\,8\,}\,\overrightarrow{b}\\[5pt]~~~&=&\displaystyle \frac{\,2\,}{\,3\,}{\, \small \times \,}\displaystyle \frac{\,3\,}{\,8\,}\,\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{b}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{b}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\left(\overrightarrow{a}+\overrightarrow{b}\right)\end{eqnarray}\)
また、\({\rm LP:PM}=s:1-s\) より、
\(\begin{eqnarray}~~~{\rm LP:PM}&=&\displaystyle \frac{\,5\,}{\,8\,}:\displaystyle \frac{\,3\,}{\,8\,}\\[5pt]~~~&=&5:3\end{eqnarray}\)
また、\({\rm OP:PN}=t:1-t\) より、
\(\begin{eqnarray}~~~{\rm OP:PN}&=&\displaystyle \frac{\,1\,}{\,2\,}:\displaystyle \frac{\,1\,}{\,2\,}\\[5pt]~~~&=&1:1\end{eqnarray}\)
問題アーカイブ05
問題アーカイブ05\(\triangle {\rm ABC}\) において、辺 \({\rm AB}\) を \(4:3\) に内分する点を \(\rm M\) 、辺 \({\rm AC}\) を \(5:3\) に内分する点を \(\rm N\) とし、線分 \({\rm BN}\) と \({\rm CM}\) の交点を \(\rm P\) とする。
\({\small (1)}~\)\(\overrightarrow{\rm AP}\) を \(\overrightarrow{\rm AB}\) 、\(\overrightarrow{\rm AC}\) で表せ。
\({\small (2)}~\)直線 \({\rm AP}\) と辺 \({\rm BC}\) の交点を \(\rm Q\) とするとき、\({\rm BQ:QC}\) および \({\rm AP:PQ}\) を求めよ。
\({\small (1)}~\)\(\overrightarrow{\rm AP}\) を \(\overrightarrow{\rm AB}\) 、\(\overrightarrow{\rm AC}\) で表せ。
\({\small (2)}~\)直線 \({\rm AP}\) と辺 \({\rm BC}\) の交点を \(\rm Q\) とするとき、\({\rm BQ:QC}\) および \({\rm AP:PQ}\) を求めよ。
東京書籍|Standard数学C[702] p.68 Level Up 5
\({\small (1)}~\)
\({\rm BP:PN}=s:1-s \) とおくと、
\(\triangle { \rm ABN }\) において、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&(1-s)\cdot\overrightarrow{\rm AB}+s\cdot\overrightarrow{\rm AN}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm AN}=\displaystyle \frac{\,5\,}{\,8\,}\overrightarrow{\rm AC}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&(1-s)\,\overrightarrow{\rm AB}+\displaystyle \frac{\,5\,}{\,8\,}s\,\overrightarrow{\rm AC}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
次に \({\rm CP:PM}=t:1-t\) とおくと、
\(\triangle { \rm ACM }\) において、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&(1-t)\cdot\overrightarrow{\rm AC}+t\cdot\overrightarrow{\rm AM}\end{eqnarray}\)
ここで、\(\overrightarrow{\rm AM}=\displaystyle \frac{\,4\,}{\,7\,}\overrightarrow{\rm AB}\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,4\,}{\,7\,}t\,\overrightarrow{\rm AB}+(1-t)\,\overrightarrow{\rm AC}~ ~ ~ \cdots {\small [\,2\,]}\end{eqnarray}\)
\({\small [\,1\,]}~,~{\small [\,2\,]}\) より、
\(\overrightarrow{\rm AB}\neq \overrightarrow{0}~,~\overrightarrow{\rm AC}\neq \overrightarrow{0}\) かつ \(\overrightarrow{\rm AB}\) と \(\overrightarrow{\rm AC}\) が平行でないので、係数を比較すると、
\(\begin{eqnarray}~~~1-s&=&\displaystyle \frac{\,4\,}{\,7\,}t~ ~ ~ ~\,\cdots {\small [\,3\,]}\\[5pt]~~~\displaystyle \frac{\,5\,}{\,8\,}s&=&1-t~ ~ ~ \cdots {\small [\,4\,]}\end{eqnarray}\)
\({\small [\,3\,]}\) より \(s=1-\displaystyle \frac{\,4\,}{\,7\,}t\) を \({\small [\,4\,]}\) に代入すると、
\(\begin{eqnarray}~~~\displaystyle \frac{\,5\,}{\,8\,}\left(1-\displaystyle \frac{\,4\,}{\,7\,}t\right)&=&1-t\\[5pt]~~~\displaystyle \frac{\,5\,}{\,8\,}-\displaystyle \frac{\,5\,}{\,14\,}t&=&1-t\\[5pt]~~~t-\displaystyle \frac{\,5\,}{\,14\,}t&=&1-\displaystyle \frac{\,5\,}{\,8\,}\\[5pt]~~~\displaystyle \frac{\,9\,}{\,14\,}t&=&\displaystyle \frac{\,3\,}{\,8\,}\\[5pt]~~~t&=&\displaystyle \frac{\,3\,}{\,8\,}{\, \small \times \,}\displaystyle \frac{\,14\,}{\,9\,}\\[5pt]~~~t&=&\displaystyle \frac{\,7\,}{\,12\,}\end{eqnarray}\)
\({\small [\,2\,]}\) に代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\displaystyle \frac{\,4\,}{\,7\,}{\, \small \times \,}\displaystyle \frac{\,7\,}{\,12\,}\,\overrightarrow{\rm AB}+\left(1-\displaystyle \frac{\,7\,}{\,12\,}\right)\overrightarrow{\rm AC}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{\rm AB}+\displaystyle \frac{\,5\,}{\,12\,}\overrightarrow{\rm AC}\end{eqnarray}\)
\({\small (2)}~\)点 \(\rm Q\) は直線 \(\rm AP\) 上にあるので、\(\overrightarrow{\rm AQ}=k\,\overrightarrow{\rm AP}\) となり、
\(\begin{eqnarray}~~~\overrightarrow{\rm AQ}&=&k\,\overrightarrow{\rm AP}\\[5pt]~~~&=&k\left(\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{\rm AB}+\displaystyle \frac{\,5\,}{\,12\,}\overrightarrow{\rm AC}\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}k\,\overrightarrow{\rm AB}+\displaystyle \frac{\,5\,}{\,12\,}k\,\overrightarrow{\rm AC}~ ~ ~ \cdots {\small [\,5\,]}\end{eqnarray}\)
また、\(\rm Q\) は辺 \(\rm BC\) 上にあり、係数の和が \(1\) となるので、
\(\begin{eqnarray}~~~\displaystyle \frac{\,1\,}{\,3\,}k+\displaystyle \frac{\,5\,}{\,12\,}k&=&1\\[5pt]~~~\displaystyle \frac{\,4\,}{\,12\,}k+\displaystyle \frac{\,5\,}{\,12\,}k&=&1\\[5pt]~~~\displaystyle \frac{\,9\,}{\,12\,}k&=&1\\[5pt]~~~k&=&\displaystyle \frac{\,4\,}{\,3\,}\end{eqnarray}\)
よって、\(\overrightarrow{\rm AQ}=\displaystyle \frac{\,4\,}{\,3\,}\overrightarrow{\rm AP}\) となる
これより、\({\rm AP:AQ}=3:4\) となるので、
\({\rm AP:PQ}=3:1\) となる
次に、\({\small [\,5\,]}\) に \(k=\displaystyle \frac{\,4\,}{\,3\,}\) を代入すると、
\(\begin{eqnarray}~~~\overrightarrow{\rm AQ}&=&\displaystyle \frac{\,1\,}{\,3\,}{\, \small \times \,}\displaystyle \frac{\,4\,}{\,3\,}\,\overrightarrow{\rm AB}+\displaystyle \frac{\,5\,}{\,12\,}{\, \small \times \,}\displaystyle \frac{\,4\,}{\,3\,}\,\overrightarrow{\rm AC}\\[5pt]~~~&=&\displaystyle \frac{\,4\,}{\,9\,}\overrightarrow{\rm AB}+\displaystyle \frac{\,5\,}{\,9\,}\overrightarrow{\rm AC}\\[5pt]~~~&=&\displaystyle \frac{\,4\overrightarrow{\rm AB}+5\overrightarrow{\rm AC}\,}{\,4+5\,}\end{eqnarray}\)
内分の式より、\({\rm BQ:QC}=5:4\) となる