- 数学C|平面上のベクトル「中心と半径が条件の円のベクトル方程式」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|中心と半径が条件の円のベクトル方程式
平面上のベクトル 65定点 \({\rm A}(\overrightarrow{a})\) と任意の点 \({\rm P}(\overrightarrow{p})\) について、
ベクトル方程式 \(|\,2\overrightarrow{p}-4\overrightarrow{a}\,|=6\) はどのような円を表すか?
ベクトル方程式 \(|\,2\overrightarrow{p}-4\overrightarrow{a}\,|=6\) はどのような円を表すか?
高校数学C|平面上のベクトル
解法のPoint
中心と半径が条件の円のベクトル方程式
Point:中心と半径が条件の円のベクトル方程式

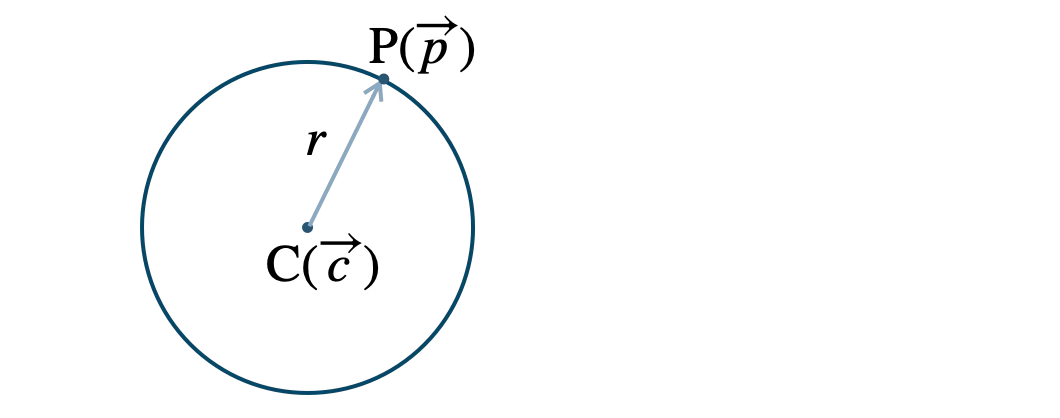
円上の任意の点を \({\rm P}(\overrightarrow{p})\) とすると、中心 \({\rm C}\) と点 \({\rm P}\) を結ぶ距離は常に \(r\) より、
\(\begin{eqnarray}~~~|\,\overrightarrow{\rm CP}\,|&=&r\end{eqnarray}\)
よって、
\(|\,\overrightarrow{p}-\overrightarrow{c}\,|=r\)
点 \({\rm C}(\overrightarrow{c})\) を中心とする、半径 \(r\) の円のベクトル方程式は、


円上の任意の点を \({\rm P}(\overrightarrow{p})\) とすると、中心 \({\rm C}\) と点 \({\rm P}\) を結ぶ距離は常に \(r\) より、
\(\begin{eqnarray}~~~|\,\overrightarrow{\rm CP}\,|&=&r\end{eqnarray}\)
よって、
\(|\,\overrightarrow{p}-\overrightarrow{c}\,|=r\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|中心と半径が条件の円のベクトル方程式
平面上のベクトル 65
定点 \({\rm A}(\overrightarrow{a})\) と任意の点 \({\rm P}(\overrightarrow{p})\) について、
ベクトル方程式 \(|\,2\overrightarrow{p}-4\overrightarrow{a}\,|=6\) はどのような円を表すか?
高校数学C|平面上のベクトル
\(\begin{eqnarray}~~~|\,2\overrightarrow{p}-4\overrightarrow{a}\,|&=&6
\\[3pt]~~~|\,2(\overrightarrow{p}-2\overrightarrow{a})\,|&=&6
\\[3pt]~~~2|\,\overrightarrow{p}-2\overrightarrow{a}\,|&=&6\end{eqnarray}\)
両辺を \(2\) で割ると、
\(\begin{eqnarray}~~~\displaystyle \frac{\,2|\,\overrightarrow{p}-2\overrightarrow{a}\,|\,}{\,2\,}&=&\displaystyle \frac{\,6\,}{\,2\,}
\\[5pt]~~~|\,\overrightarrow{p}-2\overrightarrow{a}\,|&=&3
\end{eqnarray}\)
これより、点 \((2\overrightarrow{a})\) を中心、半径 \(3\) の円を表す



