- 数学C|平面上のベクトル「大きさや内積の条件とベクトル方程式」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|大きさや内積の条件とベクトル方程式
高校数学C|平面上のベクトル
解法のPoint
大きさや内積の条件とベクトル方程式
大きさや内積の条件が与えられたときのベクトル方程式は、
\(\small [\,1\,]\) \(|\,\overrightarrow{p}-\overrightarrow{a}\,|=|\,\overrightarrow{a}\,|\)
中心 \({\rm A}(\overrightarrow{a})\)、半径 \(|\,\overrightarrow{a}\,|\) の円となる。
特に、\(|\,\overrightarrow{p}\,|=|\,\overrightarrow{a}\,|\) のときは、
点 \({\rm O}\) が中心で、半径 \(|\,\overrightarrow{a}\,|\) の円となる。
\(\small [\,2\,]\) \(\overrightarrow{p}\cdot\overrightarrow{a}=0\)
内積が \(0\) であるので、\(\overrightarrow{\rm OP}\perp\overrightarrow{\rm OA}\) となり、
点 \({\rm O}\) を通り、直線 \({\rm OA}\) に垂直な直線となる。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|大きさや内積の条件とベクトル方程式
定点 \({\rm A}(\overrightarrow{a})\) と任意の点 \({\rm P}(\overrightarrow{p})\) について、ベクトル方程式 \(|\,2\overrightarrow{p}-\overrightarrow{a}\,|=|\,\overrightarrow{a}\,|\)、\(|\,\overrightarrow{p}+\overrightarrow{a}\,|=|\,\overrightarrow{p}-\overrightarrow{a}\,|\)、\((\overrightarrow{p}+\overrightarrow{a})\cdot(\overrightarrow{p}-\overrightarrow{a})=0\) はそれぞれどのような図形を表すか?
高校数学C|平面上のベクトル
\(\begin{eqnarray}~~~|\,2\overrightarrow{p}-\overrightarrow{a}\,|&=&|\,\overrightarrow{a}\,|
\\[5pt]~~~2\,\left|\,\overrightarrow{p}-\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}\,\right|&=&|\,\overrightarrow{a}\,|
\end{eqnarray}\)
両辺を \(2\) で割ると、
\(\begin{eqnarray}~~~\left|\,\overrightarrow{p}-\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}\,\right|&=&\displaystyle \frac{\,|\,\overrightarrow{a}\,|\,}{\,2\,}\end{eqnarray}\)
よって、中心 \(\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}\right)\)、半径 \(\displaystyle \frac{\,|\,\overrightarrow{a}\,|\,}{\,2\,}\) の円となる
\(|\,\overrightarrow{p}+\overrightarrow{a}\,|=|\,\overrightarrow{p}-\overrightarrow{a}\,|\) の両辺を2乗すると、
\\[3pt]~~~(\overrightarrow{p}+\overrightarrow{a})\cdot(\overrightarrow{p}+\overrightarrow{a})&=&(\overrightarrow{p}-\overrightarrow{a})\cdot(\overrightarrow{p}-\overrightarrow{a})
\\[3pt]~~~|\,\overrightarrow{p}\,|^{2}+2\,\overrightarrow{p}\cdot\overrightarrow{a}+|\,\overrightarrow{a}\,|^{2}&=&|\,\overrightarrow{p}\,|^{2}-2\,\overrightarrow{p}\cdot\overrightarrow{a}+|\,\overrightarrow{a}\,|^{2}
\\[3pt]~~~~4\,\overrightarrow{p}\cdot\overrightarrow{a}&=&0
\\[3pt]~~~~\overrightarrow{p}\cdot\overrightarrow{a}&=&0
\end{eqnarray}\)
※ 数式は横にスクロールできます。
\(\overrightarrow{\rm OP}\) と \(\overrightarrow{\rm OA}\) の内積が \(0\) であるので、\(\overrightarrow{\rm OP}\perp\overrightarrow{\rm OA}\)
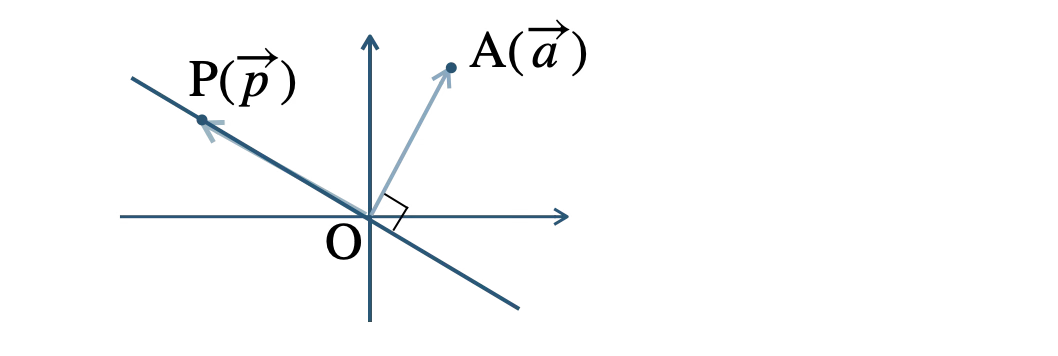

よって、点 \({\rm O}\) を通り、直線 \({\rm OA}\) に垂直な直線となる
\(\begin{eqnarray}~~~(\overrightarrow{p}+\overrightarrow{a})\cdot(\overrightarrow{p}-\overrightarrow{a})&=&0
\\[3pt]~~~|\,\overrightarrow{p}\,|^{2}-|\,\overrightarrow{a}\,|^{2}&=&0
\\[3pt]~~~|\,\overrightarrow{p}\,|^{2}&=&|\,\overrightarrow{a}\,|^{2}
\\[3pt]~~~|\,\overrightarrow{p}\,|&=&|\,\overrightarrow{a}\,|
\end{eqnarray}\)
よって、点 \({\rm O}\) が中心で、半径 \(|\,\overrightarrow{a}\,|\) の円となる



