平行六面体とベクトルの加法・減法

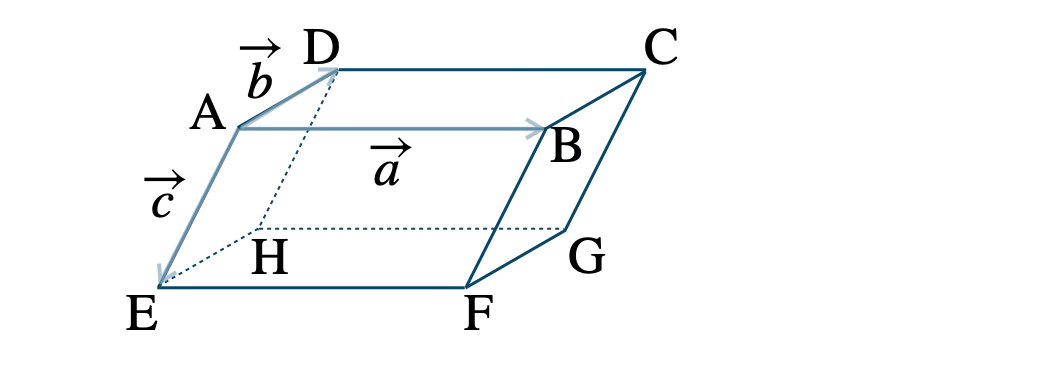
\(\overrightarrow{\rm AG}\) は、点 \({\rm A}\) → \({\rm B}\) → \({\rm C}\) → \({\rm G}\) と進んでいき、

---

---

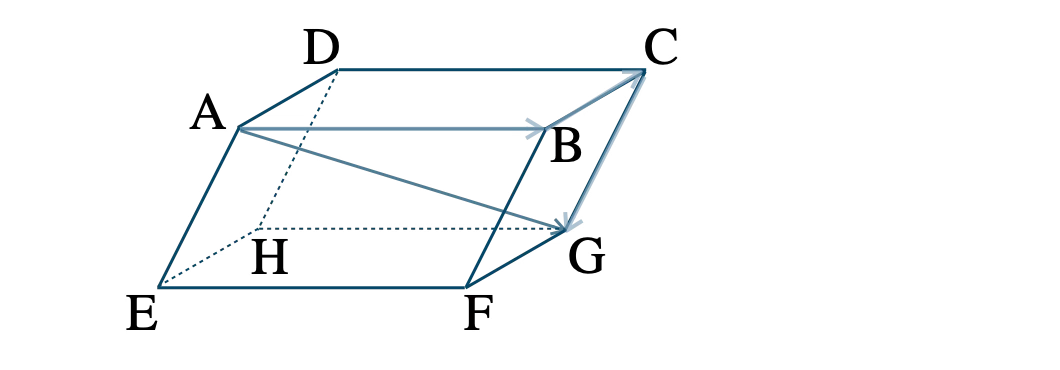
\(\begin{eqnarray}~~~\overrightarrow{\rm AG}&=&\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CG}
\\[5pt]~~~&=&\overrightarrow{\rm AB}+\overrightarrow{\rm AD}+\overrightarrow{\rm AE}
\\[5pt]~~~&=&\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\end{eqnarray}\)

 

\(\overrightarrow{\rm FD}\) は、点 \({\rm F}\) → \({\rm E}\) → \({\rm H}\) → \({\rm D}\) と進んでいき、

---

---

\(\begin{eqnarray}~~~\overrightarrow{\rm FD}&=&\overrightarrow{\rm FE}+\overrightarrow{\rm EH}+\overrightarrow{\rm HD}
\\[5pt]~~~&=&-\overrightarrow{\rm AB}+\overrightarrow{\rm AD}-\overrightarrow{\rm AE}
\\[5pt]~~~&=&-\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}\end{eqnarray}\)

 

\(\overrightarrow{\rm CE}\) は、点 \({\rm C}\) → \({\rm D}\) → \({\rm A}\) → \({\rm E}\) と進んでいき、

---

---

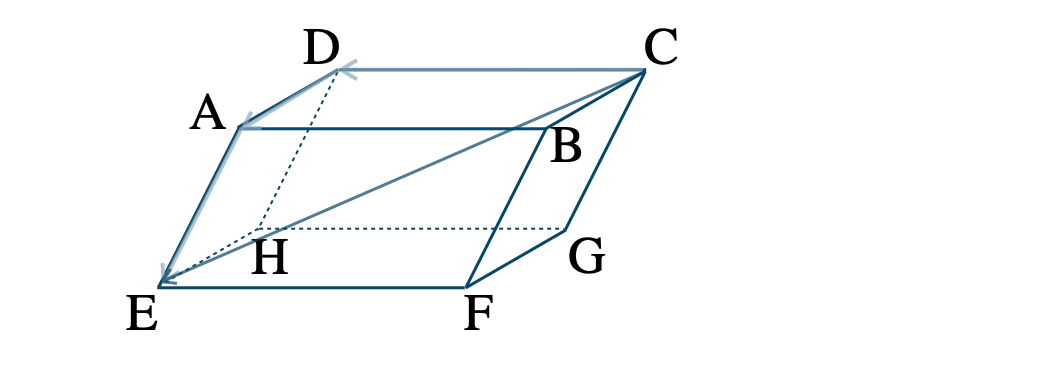
\(\begin{eqnarray}~~~\overrightarrow{\rm CE}&=&\overrightarrow{\rm CD}+\overrightarrow{\rm DA}+\overrightarrow{\rm AE}
\\[5pt]~~~&=&-\overrightarrow{\rm AB}-\overrightarrow{\rm AD}+\overrightarrow{\rm AE}
\\[5pt]~~~&=&-\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}\end{eqnarray}\)