- 数学C|空間ベクトル「四面体におけるベクトルの表し方」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|四面体におけるベクトルの表し方
空間ベクトル 09☆四面体 \(\rm ABCD \) において、辺 \(\rm BC \) の中点を \(\rm P \) 、辺 \(\rm CD \) の中点を \(\rm Q \) として、\( \overrightarrow{\rm AB}=\overrightarrow{a}~,~\)\( \overrightarrow{\rm AP}=\overrightarrow{b}~,~\)\( \overrightarrow{\rm CQ}=\overrightarrow{c} \) とするとき、\( \overrightarrow{\rm BP}~,~\)\( \overrightarrow{\rm AC}~,~\)\( \overrightarrow{\rm BD}~,~\)\( \overrightarrow{\rm AD} \) の表し方は?
高校数学C|空間ベクトル
解法のPoint
四面体におけるベクトルの表し方
Point:四面体におけるベクトルの表し方
同一平面になく、平行でない3つのベクトル \( \overrightarrow{a} ~,~ \overrightarrow{b} ~,~ \overrightarrow{c} \) を用いて、四面体の2点を結ぶベクトルを表すことができる。



\( \overrightarrow{\rm BP}=\overrightarrow{\rm AP}-\overrightarrow{\rm AB}=\overrightarrow{b}-\overrightarrow{a} \)
四面体におけるベクトルは、
同一平面になく、平行でない3つのベクトル \( \overrightarrow{a} ~,~ \overrightarrow{b} ~,~ \overrightarrow{c} \) を用いて、四面体の2点を結ぶベクトルを表すことができる。



\( \overrightarrow{\rm BP}=\overrightarrow{\rm AP}-\overrightarrow{\rm AB}=\overrightarrow{b}-\overrightarrow{a} \)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|四面体におけるベクトルの表し方
空間ベクトル 09☆
四面体 \(\rm ABCD \) において、辺 \(\rm BC \) の中点を \(\rm P \) 、辺 \(\rm CD \) の中点を \(\rm Q \) として、\( \overrightarrow{\rm AB}=\overrightarrow{a}~,~\)\( \overrightarrow{\rm AP}=\overrightarrow{b}~,~\)\( \overrightarrow{\rm CQ}=\overrightarrow{c} \) とするとき、\( \overrightarrow{\rm BP}~,~\)\( \overrightarrow{\rm AC}~,~\)\( \overrightarrow{\rm BD}~,~\)\( \overrightarrow{\rm AD} \) の表し方は?
高校数学C|空間ベクトル

\(\overrightarrow{\rm BP}\) は、ベクトルの差より、



\(\begin{eqnarray}~~~\overrightarrow{\rm BP}&=&\overrightarrow{\rm AP}-\overrightarrow{\rm AB}
\\[5pt]~~~&=&\overrightarrow{b}-\overrightarrow{a}\end{eqnarray}\)
※ 矢印の先の \({\rm P}\) が先にくる。
\(\overrightarrow{\rm AC}\) は、点 \({\rm A}\) → \({\rm B}\) → \({\rm C}\) と進んでいき、
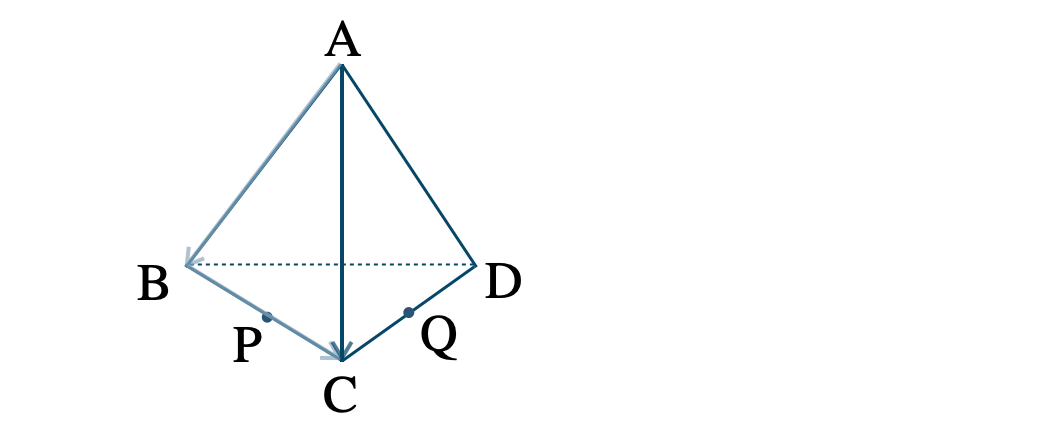

\(\begin{eqnarray}~~~\overrightarrow{\rm AC}&=&\overrightarrow{\rm AB}+\overrightarrow{\rm BC}
\\[5pt]~~~&=&\overrightarrow{\rm AB}+2\overrightarrow{\rm BP}
\\[5pt]~~~&=&\overrightarrow{a}+2(\overrightarrow{b}-\overrightarrow{a})
\\[5pt]~~~&=&\overrightarrow{a}+2\overrightarrow{b}-2\overrightarrow{a}
\\[5pt]~~~&=&2\overrightarrow{b}-\overrightarrow{a}\end{eqnarray}\)
\(\overrightarrow{\rm BD}\) は、点 \({\rm B}\) → \({\rm C}\) → \({\rm D}\) と進んでいき、


\(\begin{eqnarray}~~~\overrightarrow{\rm BD}&=&\overrightarrow{\rm BC}+\overrightarrow{\rm CD}
\\[5pt]~~~&=&2\overrightarrow{\rm BP}+2\overrightarrow{\rm CQ}
\\[5pt]~~~&=&2(\overrightarrow{b}-\overrightarrow{a})+2\overrightarrow{c}
\\[5pt]~~~&=&-2\overrightarrow{a}+2\overrightarrow{b}+2\overrightarrow{c}\end{eqnarray}\)
\(\overrightarrow{\rm AD}\) は、点 \({\rm A}\) → \({\rm B}\) → \({\rm C}\) → \({\rm D}\) と進んでいき、
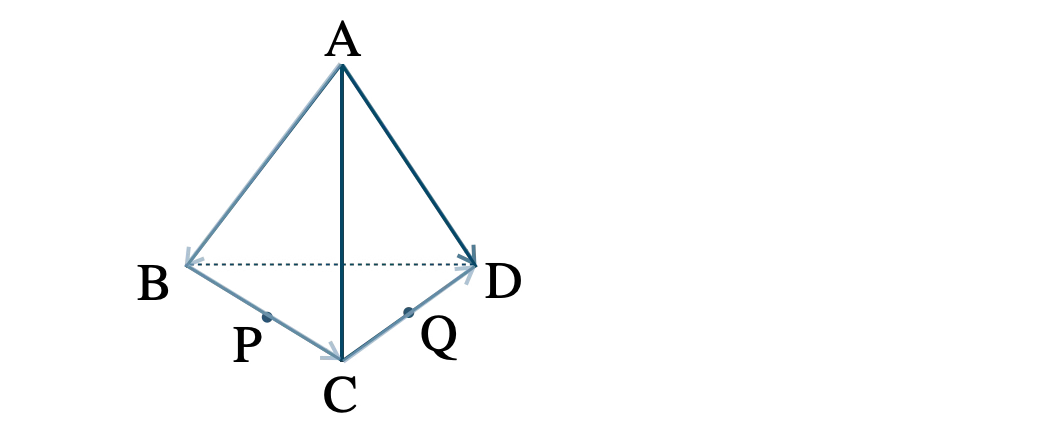

\(\begin{eqnarray}~~~\overrightarrow{\rm AD}&=&\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CD}
\\[5pt]~~~&=&\overrightarrow{\rm AB}+2\overrightarrow{\rm BP}+2\overrightarrow{\rm CQ}
\\[5pt]~~~&=&\overrightarrow{a}+2(\overrightarrow{b}-\overrightarrow{a})+2\overrightarrow{c}
\\[5pt]~~~&=&\overrightarrow{a}+2\overrightarrow{b}-2\overrightarrow{a}+2\overrightarrow{c}
\\[5pt]~~~&=&-\overrightarrow{a}+2\overrightarrow{b}+2\overrightarrow{c}\end{eqnarray}\)



