- 数学C|空間ベクトル「空間ベクトルの内積計算」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|空間ベクトルの内積計算
高校数学C|空間ベクトル
解法のPoint
空間ベクトルの内積計算
空間図形におけるベクトルの内積の求め方は、
① 内積を求めたい2つのベクトルを含む平面をピックアップする。
\( \overrightarrow{\rm AC}\cdot \overrightarrow{\rm CF} \) では、
正三角形 \( \rm ACF \) をピックアップする。
② 2つのベクトルの大きさと、始点を揃えたときのなす角 \( \theta \) を調べる。
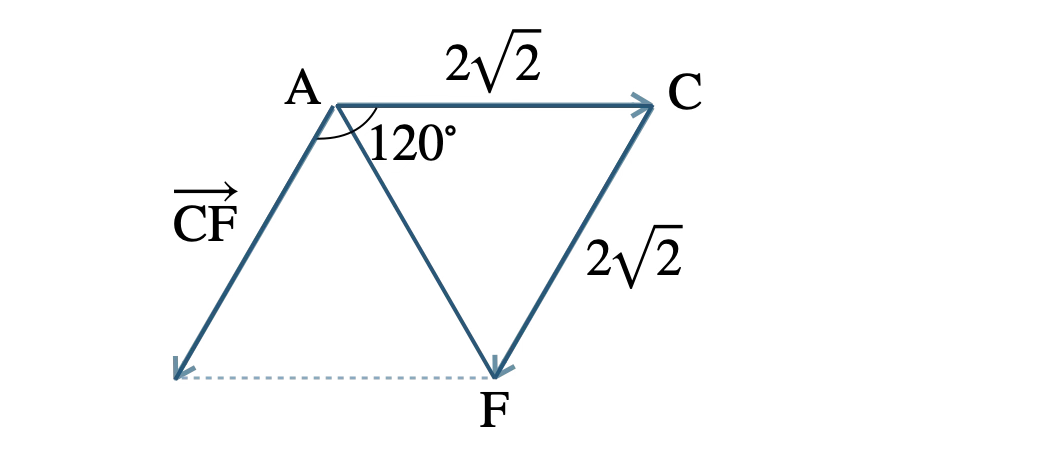


\( |\,\overrightarrow{\rm AC}\,|=2\sqrt{2}~,~|\,\overrightarrow{\rm CF}\,|=2\sqrt{2}~,~\theta=120^{\circ} \)
③ 大きさ×大きさ×なす角の \( \cos \) より内積を求める。
\( \overrightarrow{\rm AC}\cdot \overrightarrow{\rm CF} =|\,\overrightarrow{\rm AC}\,|\,|\,\overrightarrow{\rm CF}\,|\cos \theta\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|空間ベクトルの内積計算
1辺の長さ \( 2 \) の立方体 \(\rm ABCD-EFGH \) において、内積 \( \overrightarrow{\rm AB} \cdot \overrightarrow{\rm AC}~,~\)\( \overrightarrow{\rm AF} \cdot \overrightarrow{\rm AD}~,~\)\( \overrightarrow{\rm AF} \cdot \overrightarrow{\rm AH}~,~\)\(\overrightarrow{\rm AF} \cdot \overrightarrow{\rm GD}~,~\)\(\overrightarrow{\rm AC} \cdot \overrightarrow{\rm CF} \) の求め方は?
高校数学C|空間ベクトル
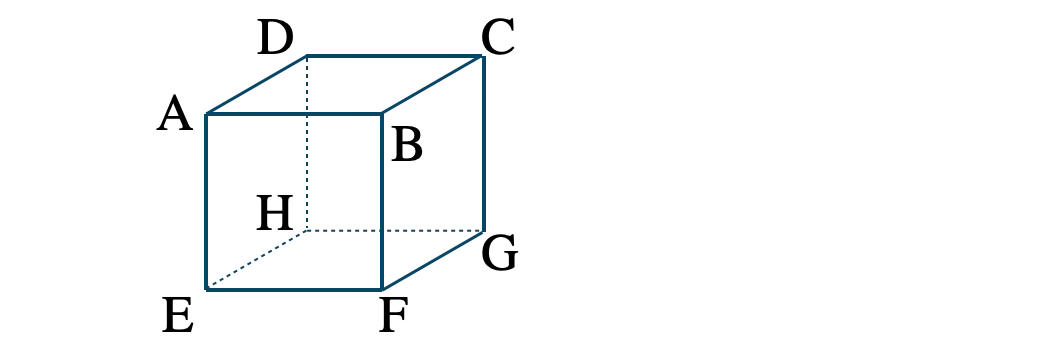
正方形 \( \rm ABCD \) において、


\( |\,\overrightarrow{\rm AB}\,|=2~,~|\,\overrightarrow{\rm AC}\,|=2\sqrt{2} \)
なす角 \( \theta \) が \( 45^{\circ} \) より、
\(\begin{eqnarray}\overrightarrow{\rm AB} \cdot \overrightarrow{\rm AC}&=&|\,\overrightarrow{\rm AB}\,|\cdot |\,\overrightarrow{\rm AC}\,|\cdot \cos 45^{\circ}
\\[5pt]~~~&=&2\cdot 2\sqrt{2}\cdot \displaystyle \frac{\,1\,}{\,\sqrt{2}\,}
\\[5pt]~~~&=&4\end{eqnarray}\)
長方形 \( \rm AFGD \) において、
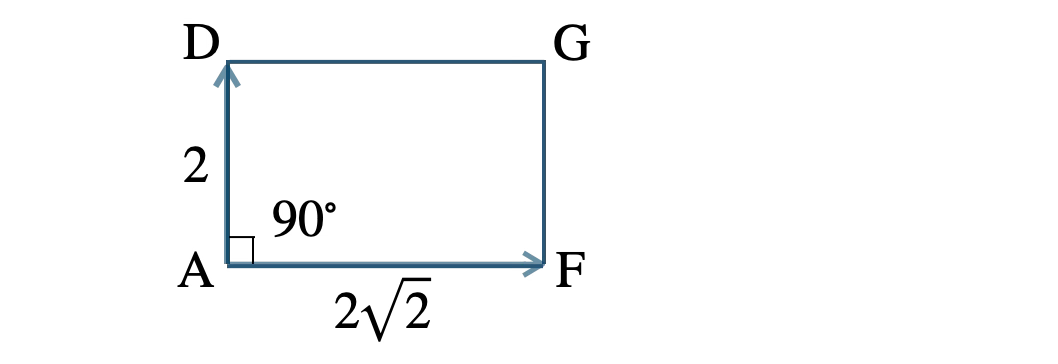

\( |\,\overrightarrow{\rm AF}\,|=2\sqrt{2}~,~|\,\overrightarrow{\rm AD}\,|=2 \)
なす角 \( \theta \) が \( 90^{\circ} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AF} \cdot \overrightarrow{\rm AD}&=&|\,\overrightarrow{\rm AF}\,|\cdot |\,\overrightarrow{\rm AD}\,|\cdot \cos \theta
\\[5pt]~~~&=&2\sqrt{2}\cdot 2\cdot 0
\\[5pt]~~~&=&0\end{eqnarray}\)
※ 垂直=内積が0となる。
正三角形 \( \rm AFH \) において、
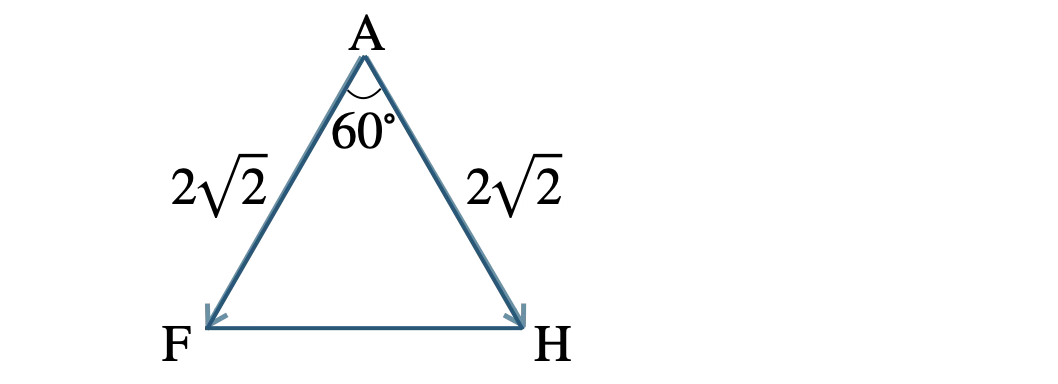

\( |\,\overrightarrow{\rm AF}\,|=2\sqrt{2}~,~|\,\overrightarrow{\rm AH}\,|=2\sqrt{2} \)
なす角 \( \theta \) が \( 60^{\circ} \) より、
\(\begin{eqnarray}\overrightarrow{\rm AF} \cdot \overrightarrow{\rm AH}&=&|\,\overrightarrow{\rm AF}\,|\cdot |\,\overrightarrow{\rm AH}\,|\cdot \cos 60^{\circ}
\\[5pt]~~~&=&2\sqrt{2}\cdot 2\sqrt{2}\cdot \displaystyle \frac{\,1\,}{\,2\,}
\\[5pt]~~~&=&4\end{eqnarray}\)
長方形 \( \rm AFGD \) において、
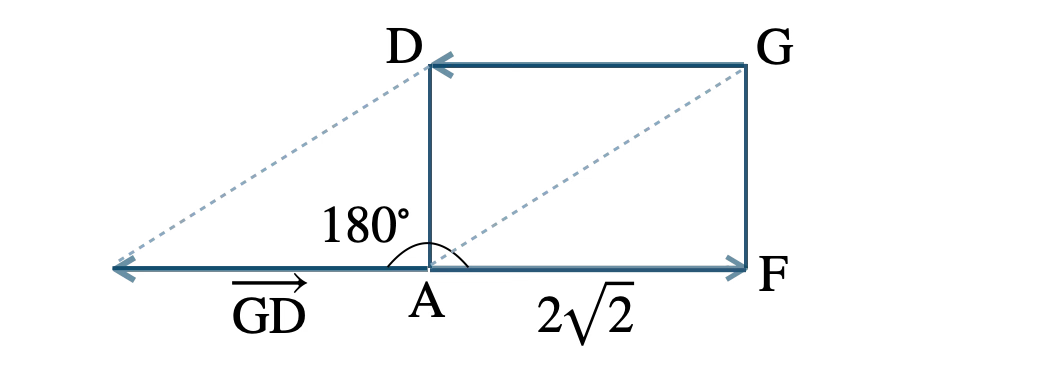

\( |\,\overrightarrow{\rm AF}\,|=2\sqrt{2}~,~|\,\overrightarrow{\rm GD}\,|=2\sqrt{2} \)
なす角 \( \theta \) は、\( \overrightarrow{\rm GD} \) を始点 \( \rm A \) に平行移動したとき、\( \theta=180^{\circ} \) となるので、
\(\begin{eqnarray} \overrightarrow{\rm AF} \cdot \overrightarrow{\rm GD}&=&|\,\overrightarrow{\rm AF}\,|\cdot |\,\overrightarrow{\rm GD}\,|\cdot \cos 180^{\circ}
\\[5pt]~~~&=&2\sqrt{2}\cdot 2\sqrt{2}\cdot (-1)
\\[5pt]~~~&=&-8\end{eqnarray}\)
正三角形 \( \rm ACF \) において、



\( |\,\overrightarrow{\rm AC}\,|=2\sqrt{2}~,~|\,\overrightarrow{\rm CF}\,|=2\sqrt{2} \)
なす角 \( \theta \) は、\( \overrightarrow{\rm CF} \) を始点 \( \rm A \) に平行移動したとき、\( \theta=120^{\circ} \) となるので、
\(\begin{eqnarray} \overrightarrow{\rm AC} \cdot \overrightarrow{\rm CF}&=&|\,\overrightarrow{\rm AC}\,|\cdot |\,\overrightarrow{\rm CF}\,|\cdot \cos 120^{\circ}
\\[5pt]~~~&=&2\sqrt{2}\cdot 2\sqrt{2}\cdot \left(\displaystyle -\frac{\,1\,}{\,2\,}\right)
\\[5pt]~~~&=&-4\end{eqnarray}\)



