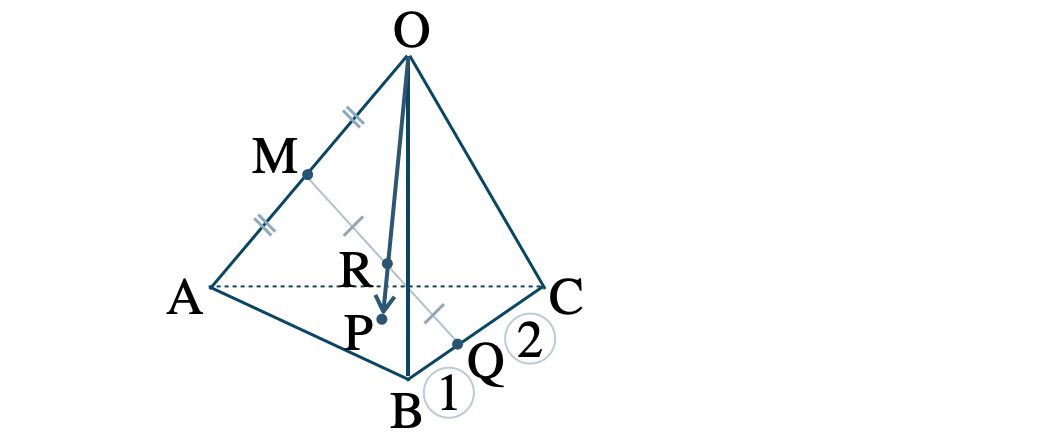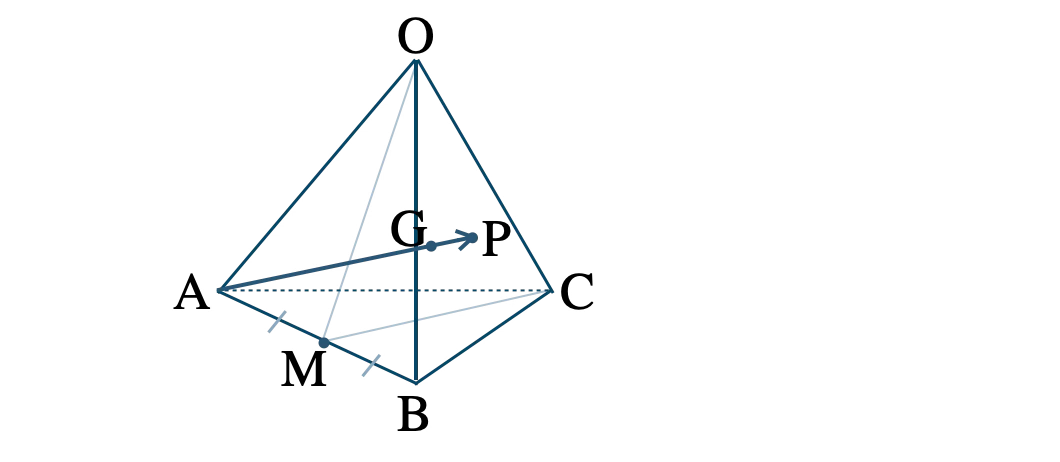このページは、「空間の直線と平面の交点のベクトル」の練習問題アーカイブページとなります。
この問題の解き方の詳細は↓
空間の直線と平面の交点のベクトル で確認できます。
問題アーカイブ01
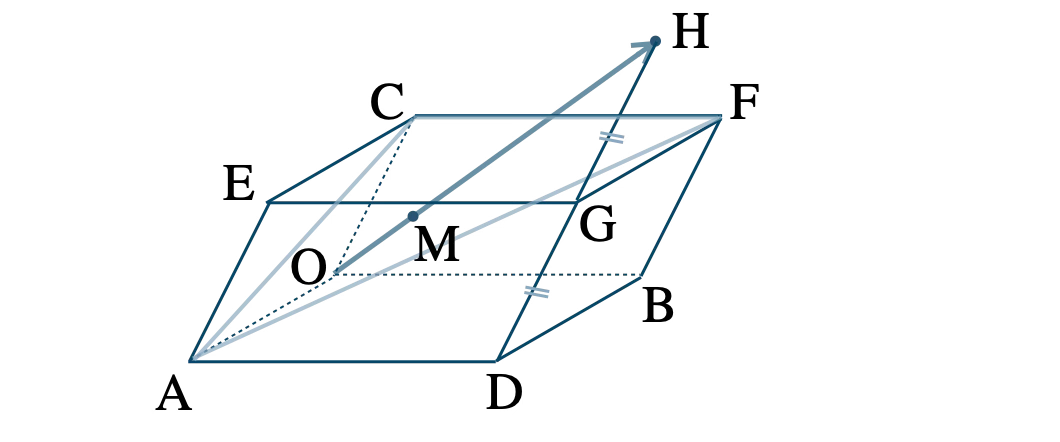
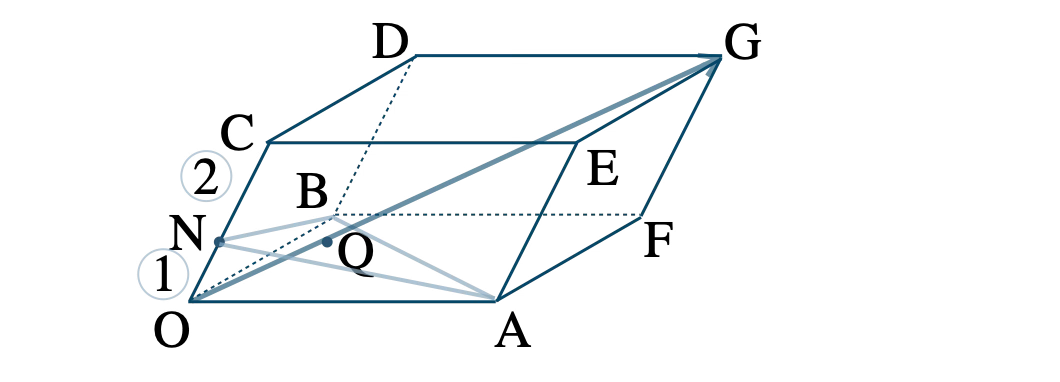
問題アーカイブ01平行六面体 \(\rm OADB-CEGF \) において、辺 \(\rm DG \) の \(\rm G \) を越える延長上に \(\rm DG=GH \) となるように点 \(\rm H \) をとる。直線 \(\rm OH \) と平面 \(\rm AFC \) との交点を \(\rm M \) とするとき、\( \overrightarrow{\rm OM} \) を \( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\)\(\overrightarrow{\rm OB}=\overrightarrow{b}~,~\)\( \overrightarrow{\rm OC}=\overrightarrow{c} \) を用いて表せ。
数研出版|数学C[708] p.69 練習20
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OH}&=&\overrightarrow{\rm OA}+\overrightarrow{\rm AD}+\overrightarrow{\rm DH}
\\[3pt]~~~&=&\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+2\overrightarrow{\rm OC}
\\[3pt]~~~&=&\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c}
\end{eqnarray}\)
ここで、点 \( \rm M \) は直線 \( \rm OH \) 上にあるので、
\( \overrightarrow{\rm OM}=k\cdot\overrightarrow{\rm OH} \) となる実数 \( k \) がある
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&k\cdot\left(\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c}\right)
\\[3pt]~~~&=&k\overrightarrow{a}+k\overrightarrow{b}+2k\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
次に、点 \( \rm M \) は平面 \( \rm AFC \) 上にあるので、
\( \overrightarrow{\rm AM}=s\overrightarrow{\rm AF}+t\overrightarrow{\rm AC} \) となる実数 \( s~,~t \) がある
始点を \( \rm O \) に揃えると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}-\overrightarrow{\rm OA}&=&s(\overrightarrow{\rm OF}-\overrightarrow{\rm OA})+t(\overrightarrow{\rm OC}-\overrightarrow{\rm OA})
\end{eqnarray}\)
ここで、\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OC}=\overrightarrow{c}\) と \(\overrightarrow{\rm OF}=\overrightarrow{\rm OB}+\overrightarrow{\rm OC}=\overrightarrow{b}+\overrightarrow{c} \) より、
\(\begin{eqnarray}~\overrightarrow{\rm OM}-\overrightarrow{a}&=&s(\overrightarrow{b}+\overrightarrow{c}-\overrightarrow{a})+t(\overrightarrow{c}-\overrightarrow{a})
\\[3pt]~\overrightarrow{\rm OM}&=&\overrightarrow{a}-s\overrightarrow{a}+s\overrightarrow{b}+s\overrightarrow{c}-t\overrightarrow{a}+t\overrightarrow{c}
\\[5pt]~\overrightarrow{\rm OM}
&=&\left(1-s-t\right)\overrightarrow{a}+s\overrightarrow{b}+(s+t)\overrightarrow{c}~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\\[3pt]~\overrightarrow{\rm OM}&=&\overrightarrow{a}-s\overrightarrow{a}+s\overrightarrow{b}+s\overrightarrow{c}-t\overrightarrow{a}+t\overrightarrow{c}
\\[5pt]~\overrightarrow{\rm OM}
&=&\left(1-s-t\right)\overrightarrow{a}+s\overrightarrow{b}+(s+t)\overrightarrow{c}~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) より、4点 \( \rm O~,~A~,~B~,~C \) は同一平面上にないので、
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}
k=1-s-t ~ ~ ~ \cdots {\small [\,3\,]} \\[5pt] k=s \hspace{33pt}~ ~ ~ \cdots {\small [\,4\,]}\\[5pt] 2k=s+t \hspace{12pt}~ ~ ~ \cdots {\small [\,5\,]}
\end{array}\right.\end{eqnarray}\)
\({\small [\,4\,]}\) より \( s=k \) を \({\small [\,5\,]}\) に代入すると、
\(\begin{eqnarray}~~~2k&=&k+t
\\[3pt]~~~t&=&k
\end{eqnarray}\)
\( s=k~,~t=k \) を \({\small [\,3\,]}\) に代入すると、
\(\begin{eqnarray}~~~k&=&1-k-k
\\[3pt]~~~3k&=&1
\\[5pt]~~~k&=&\displaystyle \frac{\,1\,}{\,3\,}
\end{eqnarray}\)
したがって、\({\small [\,1\,]}\) より
\( \overrightarrow{\rm OM}=\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{b}+\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{c} \)
問題アーカイブ02
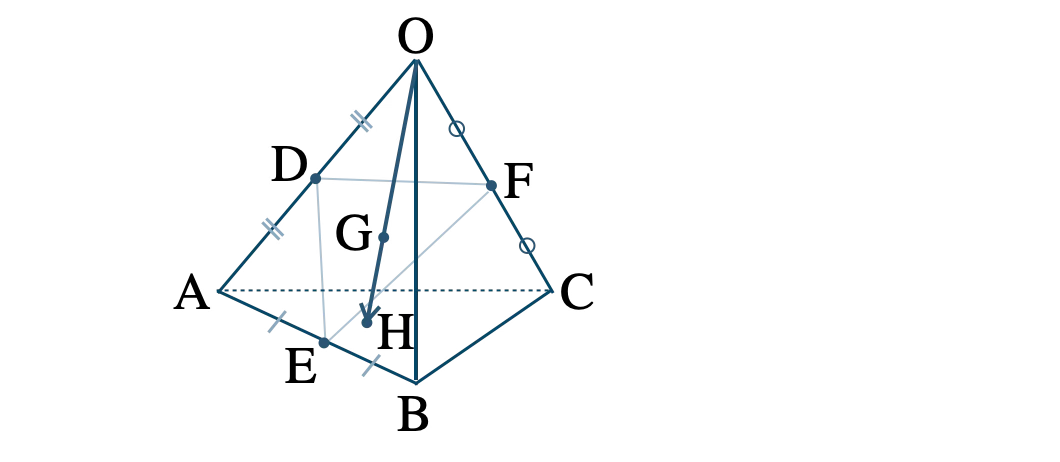
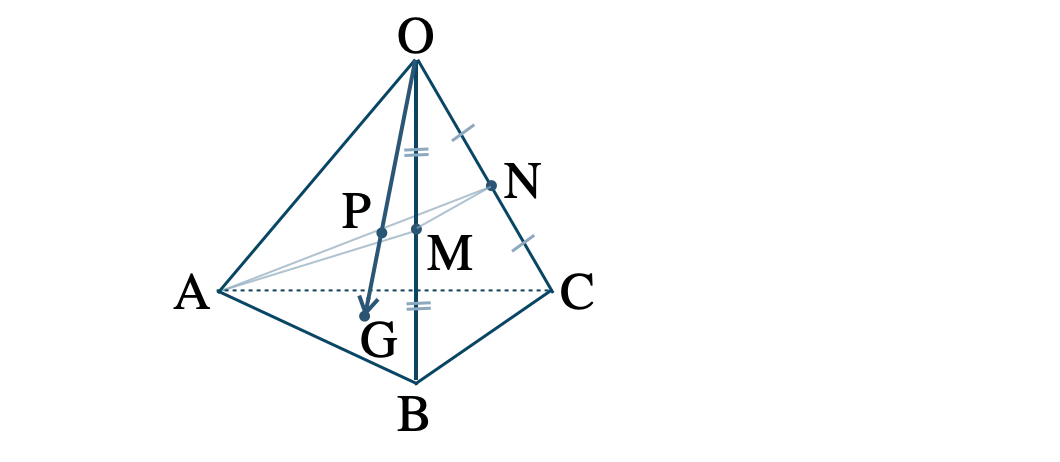
問題アーカイブ02四面体 \( {\rm OABC} \) の辺 \( {\rm OA} \) , \( {\rm AB} \) , \( {\rm OC} \) の中点を、それぞれ \( {\rm D} \) , \( {\rm E} \) , \( {\rm F} \) とし、\( \triangle{\rm DEF} \) の重心を \( {\rm G} \) 、直線 \( {\rm OG} \) と平面 \( {\rm ABC} \) の交点を \( {\rm H} \) とする。\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とするとき、\( \overrightarrow{\rm OH} \) を \( \overrightarrow{a}~,~\overrightarrow{b}~,~\overrightarrow{c} \) を用いて表せ。また、\( {\rm OG}:{\rm GH} \) を求めよ。
数研出版|数学C[708] p.80 問題 6
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OD}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OA}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}\\[5pt]~~~\overrightarrow{\rm OE}&=&\displaystyle \frac{\,1\,}{\,2\,}\left(\overrightarrow{\rm OA}+\overrightarrow{\rm OB}\right)=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}\\[5pt]~~~\overrightarrow{\rm OF}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OC}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}\end{eqnarray}\)
\( \triangle{\rm DEF} \) の重心 \( {\rm G} \) の位置ベクトルは、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\displaystyle \frac{\,1\,}{\,3\,}\left(\overrightarrow{\rm OD}+\overrightarrow{\rm OE}+\overrightarrow{\rm OF}\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,6\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,6\,}\overrightarrow{c}\end{eqnarray}\)
ここで、点 \( {\rm H} \) は直線 \( {\rm OG} \) 上にあるので、
\( \overrightarrow{\rm OH}=k\cdot\overrightarrow{\rm OG} \) となる実数 \( k \) がある
\(\begin{eqnarray}~~~\overrightarrow{\rm OH}&=&k\cdot\left(\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,6\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,6\,}\overrightarrow{c}\right)\\[5pt]~~~&=&\displaystyle \frac{\,k\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,k\,}{\,6\,}\overrightarrow{b}+\displaystyle \frac{\,k\,}{\,6\,}\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
次に、点 \( {\rm H} \) は平面 \( {\rm ABC} \) 上にあるので、
\( \overrightarrow{\rm AH}=s\overrightarrow{\rm AB}+t\overrightarrow{\rm AC} \) となる実数 \( s~,~t \) がある
始点を \( {\rm O} \) に揃えると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OH}-\overrightarrow{\rm OA}&=&s(\overrightarrow{\rm OB}-\overrightarrow{\rm OA})+t(\overrightarrow{\rm OC}-\overrightarrow{\rm OA})\end{eqnarray}\)
ここで、\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) より、
\(\begin{eqnarray}~\overrightarrow{\rm OH}-\overrightarrow{a}&=&s\overrightarrow{b}-s\overrightarrow{a}+t\overrightarrow{c}-t\overrightarrow{a}\\[5pt]~\overrightarrow{\rm OH}&=&\left(1-s-t\right)\overrightarrow{a}+s\overrightarrow{b}+t\overrightarrow{c}~ ~ \cdots {\small [\,2\,]}\end{eqnarray}\)
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) より、4点 \( {\rm O}~,~{\rm A}~,~{\rm B}~,~{\rm C} \) は同一平面上にないので、
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}\displaystyle \frac{\,k\,}{\,3\,}=1-s-t ~ ~ ~ \cdots {\small [\,3\,]} \\[5pt] \displaystyle \frac{\,k\,}{\,6\,}=s \hspace{33pt}~ ~ ~ \cdots {\small [\,4\,]}\\[5pt] \displaystyle \frac{\,k\,}{\,6\,}=t \hspace{33pt}~ ~ ~ \cdots {\small [\,5\,]}\end{array}\right.\end{eqnarray}\)
\({\small [\,4\,]}\) より \( s=\displaystyle \frac{\,k\,}{\,6\,} \) 、\({\small [\,5\,]}\) より \( t=\displaystyle \frac{\,k\,}{\,6\,} \) を \({\small [\,3\,]}\) に代入すると、
\(\begin{eqnarray}~~~\displaystyle \frac{\,k\,}{\,3\,}&=&1-\displaystyle \frac{\,k\,}{\,6\,}-\displaystyle \frac{\,k\,}{\,6\,}\\[5pt]~~~\displaystyle \frac{\,k\,}{\,3\,}&=&1-\displaystyle \frac{\,k\,}{\,3\,}\\[5pt]~~~\displaystyle \frac{\,2k\,}{\,3\,}&=&1\\[5pt]~~~k&=&\displaystyle \frac{\,3\,}{\,2\,}\end{eqnarray}\)
したがって、\({\small [\,1\,]}\) より
\( \overrightarrow{\rm OH}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{c} \)
また、\( \overrightarrow{\rm OH}=k\cdot\overrightarrow{\rm OG}=\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{\rm OG} \) より、
\(\begin{eqnarray}~~~{\rm OG}:{\rm OH}&=&1:\displaystyle \frac{\,3\,}{\,2\,}=2:3\end{eqnarray}\)
よって、\( {\rm OG}:{\rm GH}=2:1 \)
問題アーカイブ03
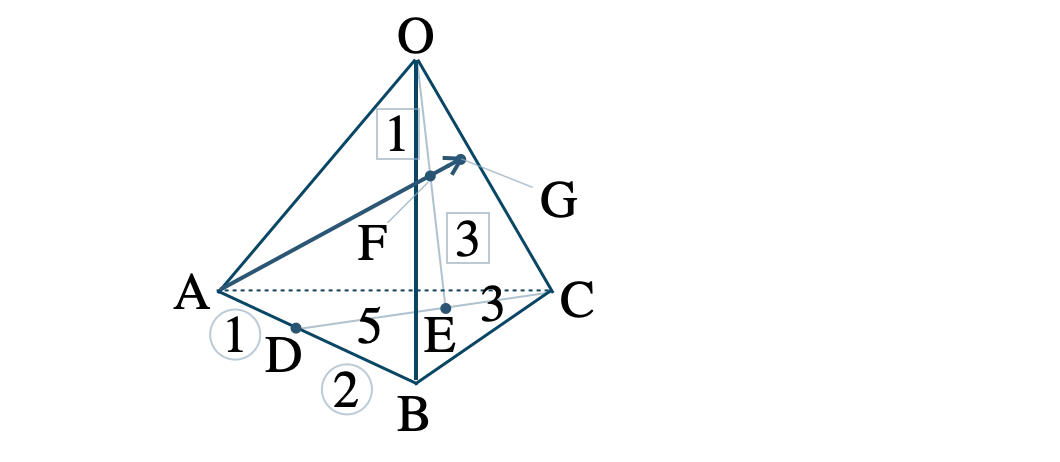
問題アーカイブ03四面体 \( {\rm OABC} \) において、辺 \( {\rm AB} \) を \( 1:2 \) に内分する点を \( {\rm D} \) 、線分 \( {\rm CD} \) を \( 3:5 \) に内分する点を \( {\rm E} \) 、線分 \( {\rm OE} \) を \( 1:3 \) に内分する点を \( {\rm F} \) とし、直線 \( {\rm AF} \) と平面 \( {\rm OBC} \) の交点を \( {\rm G} \) とする。このとき、\( {\rm AG}:{\rm FG} \) を求めよ。
数研出版|数学C[708] p.81 演習問題B 6
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とおく。
点 \( {\rm D} \) は辺 \( {\rm AB} \) を \( 1:2 \) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm OD}&=&\displaystyle \frac{\,2\cdot\overrightarrow{\rm OA}+1\cdot\overrightarrow{\rm OB}\,}{\,1+2\,}\\[5pt]~~~&=&\displaystyle \frac{\,2\overrightarrow{a}+\overrightarrow{b}\,}{\,3\,}\end{eqnarray}\)
点 \( {\rm E} \) は線分 \( {\rm CD} \) を \( 3:5 \) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm OE}&=&\displaystyle \frac{\,5\cdot\overrightarrow{\rm OC}+3\cdot\overrightarrow{\rm OD}\,}{\,3+5\,}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,8\,}\left(5\overrightarrow{c}+3\cdot\displaystyle \frac{\,2\overrightarrow{a}+\overrightarrow{b}\,}{\,3\,}\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,8\,}\left(2\overrightarrow{a}+\overrightarrow{b}+5\overrightarrow{c}\right)\end{eqnarray}\)
点 \( {\rm F} \) は線分 \( {\rm OE} \) を \( 1:3 \) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm OF}&=&\displaystyle \frac{\,3\cdot\overrightarrow{\rm OO}+1\cdot\overrightarrow{\rm OE}\,}{\,1+3\,}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{\rm OE}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,32\,}\left(2\overrightarrow{a}+\overrightarrow{b}+5\overrightarrow{c}\right)\end{eqnarray}\)
ここで、点 \( {\rm G} \) は直線 \( {\rm AF} \) 上にあるので、
\( \overrightarrow{\rm AG}=k\cdot\overrightarrow{\rm AF} \) となる実数 \( k \) がある
始点を \( {\rm O} \) に揃えると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}-\overrightarrow{\rm OA}&=&k(\overrightarrow{\rm OF}-\overrightarrow{\rm OA})\\[3pt]~~~\overrightarrow{\rm OG}&=&(1-k)\overrightarrow{\rm OA}+k\overrightarrow{\rm OF}\\[5pt]~~~&=&(1-k)\overrightarrow{a}+\displaystyle \frac{\,k\,}{\,32\,}\left(2\overrightarrow{a}+\overrightarrow{b}+5\overrightarrow{c}\right)\\[5pt]~~~&=&\left(1-k+\displaystyle \frac{\,k\,}{\,16\,}\right)\overrightarrow{a}+\displaystyle \frac{\,k\,}{\,32\,}\overrightarrow{b}+\displaystyle \frac{\,5k\,}{\,32\,}\overrightarrow{c}\\[5pt]~~~&=&\left(1-\displaystyle \frac{\,15k\,}{\,16\,}\right)\overrightarrow{a}+\displaystyle \frac{\,k\,}{\,32\,}\overrightarrow{b}+\displaystyle \frac{\,5k\,}{\,32\,}\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
次に、点 \( {\rm G} \) は平面 \( {\rm OBC} \) 上にあるので、
\( \overrightarrow{\rm OG}=s\overrightarrow{\rm OB}+t\overrightarrow{\rm OC} \) となる実数 \( s~,~t \) がある
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&s\overrightarrow{b}+t\overrightarrow{c}~ ~ ~ \cdots {\small [\,2\,]}\end{eqnarray}\)
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) より、4点 \( {\rm O}~,~{\rm A}~,~{\rm B}~,~{\rm C} \) は同一平面上にないので、
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}1-\displaystyle \frac{\,15k\,}{\,16\,}=0 ~ ~ ~ \cdots {\small [\,3\,]} \\[5pt] \displaystyle \frac{\,k\,}{\,32\,}=s \hspace{21pt}~ ~ ~ \cdots {\small [\,4\,]}\\[5pt] \displaystyle \frac{\,5k\,}{\,32\,}=t \hspace{18pt}~ ~ ~ \cdots {\small [\,5\,]}\end{array}\right.\end{eqnarray}\)
\({\small [\,3\,]}\) を解くと、
\(\begin{eqnarray}~~~1-\displaystyle \frac{\,15k\,}{\,16\,}&=&0\\[5pt]~~~\displaystyle \frac{\,15k\,}{\,16\,}&=&1\\[5pt]~~~k&=&\displaystyle \frac{\,16\,}{\,15\,}\end{eqnarray}\)
\( \overrightarrow{\rm AG}=k\cdot\overrightarrow{\rm AF}=\displaystyle \frac{\,16\,}{\,15\,}\overrightarrow{\rm AF} \) より、
\(\begin{eqnarray}~~~{\rm AG}:{\rm AF}&=&16:15\end{eqnarray}\)
よって、\( {\rm AG}:{\rm FG}=16:1 \)
問題アーカイブ04
問題アーカイブ04四面体 \(\rm OABC \) において、辺 \(\rm OA \) の中点を \(\rm M \) 、辺 \(\rm BC \) を \( 1:2 \) に内分する点を \(\rm Q \) 、線分 \(\rm MQ \) の中点を \(\rm R \) とし、直線 \(\rm OR \) と平面 \(\rm ABC \) の交点を \(\rm P \) とする。\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とするとき、\( \overrightarrow{\rm OP} \) を \( \overrightarrow{a}~,~\overrightarrow{b}~,~\overrightarrow{c} \) を用いて表せ。
数研出版|高等学校数学C[709] p.64 練習16
数研出版|新編数学C[710] p.65 練習14
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OA}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}
\end{eqnarray}\)
\(\begin{eqnarray}~~~\overrightarrow{\rm OQ}&=&\displaystyle \frac{\,2\cdot\overrightarrow{\rm OB}+1\cdot\overrightarrow{\rm OC}\,}{\,1+2\,}=\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c}
\end{eqnarray}\)
\(\begin{eqnarray}~~~\overrightarrow{\rm OR}&=&\displaystyle \frac{\,\overrightarrow{\rm OM}+\overrightarrow{\rm OQ}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,2\,}{\,3\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c}\right)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,6\,}\overrightarrow{c}
\end{eqnarray}\)
ここで、点 \( \rm P \) は直線 \( \rm OR \) 上にあるので、
\( \overrightarrow{\rm OP}=k\cdot\overrightarrow{\rm OR} \) となる実数 \( k \) がある
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&k\cdot\left(\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,6\,}\overrightarrow{c}\right)
\\[5pt]~~~&=&\displaystyle \frac{\,k\,}{\,4\,}\overrightarrow{a}+\displaystyle \frac{\,k\,}{\,3\,}\overrightarrow{b}+\displaystyle \frac{\,k\,}{\,6\,}\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
次に、点 \( \rm P \) は平面 \( \rm ABC \) 上にあるので、
\( \overrightarrow{\rm AP}=s\overrightarrow{\rm AB}+t\overrightarrow{\rm AC} \) となる実数 \( s~,~t \) がある
始点を \( \rm O \) に揃えると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}-\overrightarrow{\rm OA}&=&s(\overrightarrow{\rm OB}-\overrightarrow{\rm OA})+t(\overrightarrow{\rm OC}-\overrightarrow{\rm OA})
\end{eqnarray}\)
ここで、\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c}\) より、
\(\begin{eqnarray}~\overrightarrow{\rm OP}-\overrightarrow{a}&=&s(\overrightarrow{b}-\overrightarrow{a})+t(\overrightarrow{c}-\overrightarrow{a})
\\[3pt]~\overrightarrow{\rm OP}&=&\overrightarrow{a}-s\overrightarrow{a}-t\overrightarrow{a}+s\overrightarrow{b}+t\overrightarrow{c}
\\[3pt]~\overrightarrow{\rm OP}
&=&\left(1-s-t\right)\overrightarrow{a}+s\overrightarrow{b}+t\overrightarrow{c}~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) より、4点 \( \rm O~,~A~,~B~,~C \) は同一平面上にないので、
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}
\displaystyle \frac{\,k\,}{\,4\,}=1-s-t ~ ~ ~ \cdots {\small [\,3\,]} \\[5pt] \displaystyle \frac{\,k\,}{\,3\,}=s \hspace{33pt}~ ~ ~ \cdots {\small [\,4\,]}\\[5pt] \displaystyle \frac{\,k\,}{\,6\,}=t \hspace{33pt}~ ~ ~ \cdots {\small [\,5\,]}
\end{array}\right.\end{eqnarray}\)
\({\small [\,4\,]}\) より \( s=\displaystyle \frac{\,k\,}{\,3\,} \) 、\({\small [\,5\,]}\) より \( t=\displaystyle \frac{\,k\,}{\,6\,} \) を \({\small [\,3\,]}\) に代入すると、
\(\begin{eqnarray}~~~\displaystyle \frac{\,k\,}{\,4\,}&=&1-\displaystyle \frac{\,k\,}{\,3\,}-\displaystyle \frac{\,k\,}{\,6\,}
\\[5pt]~~~\displaystyle \frac{\,k\,}{\,4\,}+\displaystyle \frac{\,k\,}{\,3\,}+\displaystyle \frac{\,k\,}{\,6\,}&=&1
\\[5pt]~~~\displaystyle \frac{\,3k+4k+2k\,}{\,12\,}&=&1
\\[5pt]~~~\displaystyle \frac{\,9k\,}{\,12\,}&=&1
\\[5pt]~~~k&=&\displaystyle \frac{\,4\,}{\,3\,}
\end{eqnarray}\)
したがって、\({\small [\,1\,]}\) より
\( \overrightarrow{\rm OP}=\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,4\,}{\,9\,}\overrightarrow{b}+\displaystyle \frac{\,2\,}{\,9\,}\overrightarrow{c} \)
問題アーカイブ05
問題アーカイブ05四面体 \( {\rm OABC} \) において、\( \triangle{\rm ABC} \) の重心を \( {\rm G} \) 、辺 \( {\rm OB} \) の中点を \( {\rm M} \) 、辺 \( {\rm OC} \) の中点を \( {\rm N} \) とする。直線 \( {\rm OG} \) と平面 \( {\rm AMN} \) の交点を \( {\rm P} \) とするとき、\( {\rm OG}:{\rm OP} \) を求めよ。
数研出版|高等学校数学C[709] p.74 章末問題B 12
数研出版|新編数学C[710] p.73 章末問題B 11
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とおく。
点 \( {\rm G} \) は \( \triangle{\rm ABC} \) の重心なので、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\displaystyle \frac{\,1\,}{\,3\,}\left(\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC}\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\left(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\right)\end{eqnarray}\)
点 \( {\rm M} \) は辺 \( {\rm OB} \) の中点なので、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}\end{eqnarray}\)
点 \( {\rm N} \) は辺 \( {\rm OC} \) の中点なので、
\(\begin{eqnarray}~~~\overrightarrow{\rm ON}&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}\end{eqnarray}\)
ここで、点 \( {\rm P} \) は直線 \( {\rm OG} \) 上にあるので、
\( \overrightarrow{\rm OP}=k\cdot\overrightarrow{\rm OG} \) となる実数 \( k \) がある
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&k\cdot\displaystyle \frac{\,1\,}{\,3\,}\left(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\right)\\[5pt]~~~&=&\displaystyle \frac{\,k\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,k\,}{\,3\,}\overrightarrow{b}+\displaystyle \frac{\,k\,}{\,3\,}\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
次に、点 \( {\rm P} \) は平面 \( {\rm AMN} \) 上にあるので、
\( \overrightarrow{\rm AP}=s\overrightarrow{\rm AM}+t\overrightarrow{\rm AN} \) となる実数 \( s~,~t \) がある
始点を \( {\rm O} \) に揃えると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}-\overrightarrow{\rm OA}&=&s(\overrightarrow{\rm OM}-\overrightarrow{\rm OA})+t(\overrightarrow{\rm ON}-\overrightarrow{\rm OA})\end{eqnarray}\)
ここで、\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OM}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}~,~\overrightarrow{\rm ON}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c} \) より、
\(\begin{eqnarray}~\overrightarrow{\rm OP}-\overrightarrow{a}&=&s\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}-\overrightarrow{a}\right)+t\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{c}-\overrightarrow{a}\right)\\[5pt]~\overrightarrow{\rm OP}&=&\overrightarrow{a}-s\overrightarrow{a}+\displaystyle \frac{\,s\,}{\,2\,}\overrightarrow{b}-t\overrightarrow{a}+\displaystyle \frac{\,t\,}{\,2\,}\overrightarrow{c}\\[5pt]~\overrightarrow{\rm OP}&=&\left(1-s-t\right)\overrightarrow{a}+\displaystyle \frac{\,s\,}{\,2\,}\overrightarrow{b}+\displaystyle \frac{\,t\,}{\,2\,}\overrightarrow{c}~ ~ \cdots {\small [\,2\,]}\end{eqnarray}\)
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) より、4点 \( {\rm O}~,~{\rm A}~,~{\rm B}~,~{\rm C} \) は同一平面上にないので、
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}\displaystyle \frac{\,k\,}{\,3\,}=1-s-t ~ ~ ~ \cdots {\small [\,3\,]} \\[5pt] \displaystyle \frac{\,k\,}{\,3\,}=\displaystyle \frac{\,s\,}{\,2\,} \hspace{27pt}~ ~ ~ \cdots {\small [\,4\,]}\\[5pt] \displaystyle \frac{\,k\,}{\,3\,}=\displaystyle \frac{\,t\,}{\,2\,} \hspace{27pt}~ ~ ~ \cdots {\small [\,5\,]}\end{array}\right.\end{eqnarray}\)
\({\small [\,4\,]}\) より \( s=\displaystyle \frac{\,2k\,}{\,3\,} \) 、\({\small [\,5\,]}\) より \( t=\displaystyle \frac{\,2k\,}{\,3\,} \) を \({\small [\,3\,]}\) に代入すると、
\(\begin{eqnarray}~~~\displaystyle \frac{\,k\,}{\,3\,}&=&1-\displaystyle \frac{\,2k\,}{\,3\,}-\displaystyle \frac{\,2k\,}{\,3\,}\\[5pt]~~~\displaystyle \frac{\,k\,}{\,3\,}&=&1-\displaystyle \frac{\,4k\,}{\,3\,}\\[5pt]~~~\displaystyle \frac{\,5k\,}{\,3\,}&=&1\\[5pt]~~~k&=&\displaystyle \frac{\,3\,}{\,5\,}\end{eqnarray}\)
\( \overrightarrow{\rm OP}=k\cdot\overrightarrow{\rm OG}=\displaystyle \frac{\,3\,}{\,5\,}\overrightarrow{\rm OG} \) より、
\(\begin{eqnarray}~~~{\rm OP}:{\rm OG}&=&3:5\end{eqnarray}\)
よって、\( {\rm OG}:{\rm OP}=5:3 \)
問題アーカイブ06
問題アーカイブ06平行六面体 \( {\rm OAFB-CEGD} \) において、辺 \( {\rm OC} \) を \( 1:2 \) に内分する点を \( {\rm N} \) とし、対角線 \( {\rm OG} \) と平面 \( {\rm ABN} \) との交点を \( {\rm Q} \) とする。\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c}~,~\overrightarrow{\rm OQ}=\overrightarrow{q} \) とするとき、\( \overrightarrow{q} \) を \( \overrightarrow{a}~,~\overrightarrow{b}~,~\overrightarrow{c} \) で表せ。
東京書籍|Advanced数学C[701] p.62 問24
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\overrightarrow{\rm OA}+\overrightarrow{\rm AF}+\overrightarrow{\rm FG}\\[3pt]~~~&=&\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC}\\[3pt]~~~&=&\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\end{eqnarray}\)
また、点 \( {\rm N} \) は辺 \( {\rm OC} \) を \( 1:2 \) に内分するので、
\(\begin{eqnarray}~~~\overrightarrow{\rm ON}&=&\displaystyle \frac{\,1\,}{\,1+2\,}\overrightarrow{\rm OC}\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c}\end{eqnarray}\)
ここで、点 \( \rm Q \) は直線 \( \rm OG \) 上にあるので、
\( \overrightarrow{\rm OQ}=k\cdot\overrightarrow{\rm OG} \) となる実数 \( k \) がある
\(\begin{eqnarray}~~~\overrightarrow{\rm OQ}&=&k\cdot\left(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\right)\\[3pt]~~~&=&k\overrightarrow{a}+k\overrightarrow{b}+k\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
次に、点 \( \rm Q \) は平面 \( \rm ABN \) 上にあるので、
\( \overrightarrow{\rm AQ}=s\overrightarrow{\rm AB}+t\overrightarrow{\rm AN} \) となる実数 \( s~,~t \) がある
始点を \( \rm O \) に揃えると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OQ}-\overrightarrow{\rm OA}&=&s(\overrightarrow{\rm OB}-\overrightarrow{\rm OA})+t(\overrightarrow{\rm ON}-\overrightarrow{\rm OA})\end{eqnarray}\)
ここで、\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}\) と \(\overrightarrow{\rm ON}=\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OQ}-\overrightarrow{a}&=&s(\overrightarrow{b}-\overrightarrow{a})+t\left(\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c}-\overrightarrow{a}\right)\\[5pt]~\overrightarrow{\rm OQ}&=&\overrightarrow{a}-s\overrightarrow{a}+s\overrightarrow{b}-t\overrightarrow{a}+\displaystyle \frac{\,t\,}{\,3\,}\overrightarrow{c}\\[5pt]~\overrightarrow{\rm OQ}&=&\left(1-s-t\right)\overrightarrow{a}+s\overrightarrow{b}+\displaystyle \frac{\,t\,}{\,3\,}\overrightarrow{c}~ ~ \cdots {\small [\,2\,]}\end{eqnarray}\)
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) より、4点 \( \rm O~,~A~,~B~,~C \) は同一平面上にないので、
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}k=1-s-t ~ ~ ~ \cdots {\small [\,3\,]} \\[5pt] k=s \hspace{33pt}~ ~ ~ \cdots {\small [\,4\,]}\\[5pt] k=\displaystyle \frac{\,t\,}{\,3\,} \hspace{24pt}~ ~ ~ \cdots {\small [\,5\,]}\end{array}\right.\end{eqnarray}\)
\({\small [\,4\,]}\) より \( s=k \)、\({\small [\,5\,]}\) より \( t=3k \) を \({\small [\,3\,]}\) に代入すると、
\(\begin{eqnarray}~~~k&=&1-k-3k\\[3pt]~~~k&=&1-4k\\[3pt]~~~5k&=&1\\[5pt]~~~k&=&\displaystyle \frac{\,1\,}{\,5\,}\end{eqnarray}\)
したがって、\({\small [\,1\,]}\) より
\( \overrightarrow{\rm OQ}=\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{c} \)
問題アーカイブ07
問題アーカイブ07四面体 \( {\rm OABC} \) において、辺 \( {\rm AB} \) の中点を \( {\rm M} \) 、\( \triangle{\rm OMC} \) の重心を \( {\rm G} \) とし、直線 \( {\rm AG} \) と平面 \( {\rm OBC} \) との交点を \( {\rm P} \) とする。\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c}~,~\overrightarrow{\rm OP}=\overrightarrow{p} \) とするとき、\( \overrightarrow{p} \) を \( \overrightarrow{a}~,~\overrightarrow{b}~,~\overrightarrow{c} \) で表せ。
東京書籍|Advanced数学C[701] p.65 問題 19
点 \( {\rm M} \) は辺 \( {\rm AB} \) の中点なので、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,1\,}{\,2\,}\left(\overrightarrow{\rm OA}+\overrightarrow{\rm OB}\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\left(\overrightarrow{a}+\overrightarrow{b}\right)\end{eqnarray}\)
点 \( {\rm G} \) は \( \triangle{\rm OMC} \) の重心なので、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\displaystyle \frac{\,1\,}{\,3\,}\left(\overrightarrow{\rm OO}+\overrightarrow{\rm OM}+\overrightarrow{\rm OC}\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\left(\overrightarrow{0}+\displaystyle \frac{\,1\,}{\,2\,}\left(\overrightarrow{a}+\overrightarrow{b}\right)+\overrightarrow{c}\right)\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,6\,}\left(\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c}\right)\end{eqnarray}\)
ここで、点 \( {\rm P} \) は直線 \( {\rm AG} \) 上にあるので、
\( \overrightarrow{\rm AP}=k\cdot\overrightarrow{\rm AG} \) となる実数 \( k \) がある
始点を \( {\rm O} \) に揃えると、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}-\overrightarrow{\rm OA}&=&k(\overrightarrow{\rm OG}-\overrightarrow{\rm OA})\\[3pt]~~~\overrightarrow{\rm OP}&=&(1-k)\overrightarrow{\rm OA}+k\overrightarrow{\rm OG}\\[5pt]~~~&=&(1-k)\overrightarrow{a}+\displaystyle \frac{\,k\,}{\,6\,}\left(\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c}\right)\\[5pt]~~~&=&\left(1-k+\displaystyle \frac{\,k\,}{\,6\,}\right)\overrightarrow{a}+\displaystyle \frac{\,k\,}{\,6\,}\overrightarrow{b}+\displaystyle \frac{\,k\,}{\,3\,}\overrightarrow{c}\\[5pt]~~~&=&\left(1-\displaystyle \frac{\,5k\,}{\,6\,}\right)\overrightarrow{a}+\displaystyle \frac{\,k\,}{\,6\,}\overrightarrow{b}+\displaystyle \frac{\,k\,}{\,3\,}\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}\end{eqnarray}\)
次に、点 \( {\rm P} \) は平面 \( {\rm OBC} \) 上にあるので、
\( \overrightarrow{\rm OP}=s\overrightarrow{\rm OB}+t\overrightarrow{\rm OC} \) となる実数 \( s~,~t \) がある
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&s\overrightarrow{b}+t\overrightarrow{c}~ ~ ~ \cdots {\small [\,2\,]}\end{eqnarray}\)
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) より、4点 \( {\rm O}~,~{\rm A}~,~{\rm B}~,~{\rm C} \) は同一平面上にないので、
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}1-\displaystyle \frac{\,5k\,}{\,6\,}=0 ~ ~ ~ \cdots {\small [\,3\,]} \\[5pt] \displaystyle \frac{\,k\,}{\,6\,}=s \hspace{21pt}~ ~ ~ \cdots {\small [\,4\,]}\\[5pt] \displaystyle \frac{\,k\,}{\,3\,}=t \hspace{21pt}~ ~ ~ \cdots {\small [\,5\,]}\end{array}\right.\end{eqnarray}\)
\({\small [\,3\,]}\) を解くと、
\(\begin{eqnarray}~~~1-\displaystyle \frac{\,5k\,}{\,6\,}&=&0\\[5pt]~~~\displaystyle \frac{\,5k\,}{\,6\,}&=&1\\[5pt]~~~k&=&\displaystyle \frac{\,6\,}{\,5\,}\end{eqnarray}\)
\({\small [\,4\,]}\) より \( s=\displaystyle \frac{\,k\,}{\,6\,}=\displaystyle \frac{\,1\,}{\,5\,} \) 、\({\small [\,5\,]}\) より \( t=\displaystyle \frac{\,k\,}{\,3\,}=\displaystyle \frac{\,2\,}{\,5\,} \)
したがって、\({\small [\,2\,]}\) より
\( \overrightarrow{p}=\displaystyle \frac{\,1\,}{\,5\,}\overrightarrow{b}+\displaystyle \frac{\,2\,}{\,5\,}\overrightarrow{c} \)