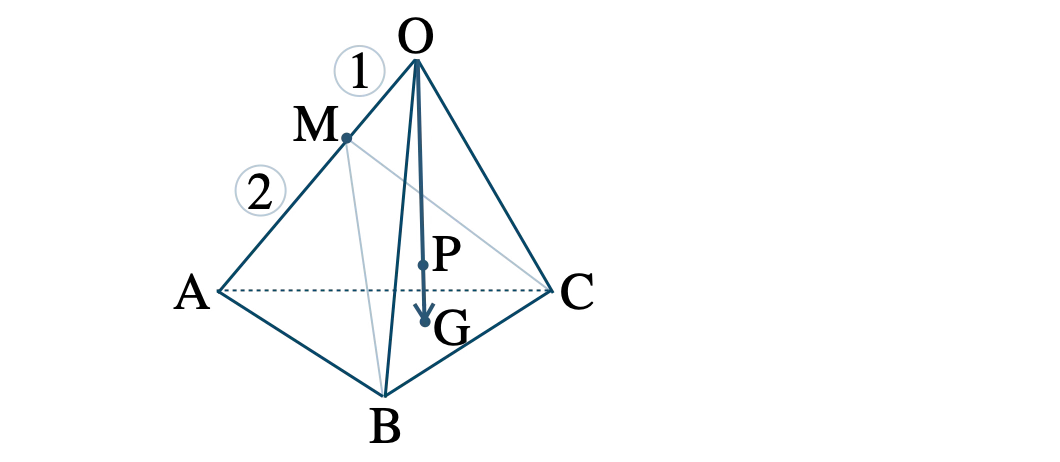このページは、「直線と平面の交点のベクトル(係数の和が1)」の練習問題アーカイブページとなります。
この問題の解き方の詳細は↓
直線と平面の交点のベクトル(係数の和が1) で確認できます。
問題アーカイブ01
問題アーカイブ01四面体 \({\rm OABC}\) において、辺 \({\rm OA}\) を \(1:2\) に内分する点を \({\rm M}\)、底面 \({\rm ABC}\) の重心を \({\rm G}\) とする。線分 \({\rm OG}\) と平面 \({\rm MBC}\) との交点を \({\rm P}\) とするとき、\({\rm OP:PG}\) を求めよ。
東京書籍|Advanced数学C[701] p.67 発展 問1
\( \overrightarrow{\rm OA}=\overrightarrow{a} ~,~ \overrightarrow{\rm OB}=\overrightarrow{b} ~,~ \overrightarrow{\rm OC}=\overrightarrow{c} \) とおくと、
\( \overrightarrow{\rm OM} \) は、\( \rm OM:MA=1:2 \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OM}&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{\rm OA}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{a}\end{eqnarray}\)
\( \overrightarrow{\rm OG} \) は、\({\rm G}\) が \( \triangle {\rm ABC} \) の重心より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\displaystyle \frac{\,\overrightarrow{\rm OA}+\overrightarrow{\rm OB}+\overrightarrow{\rm OC}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c}\end{eqnarray}\)
ここで、点 \( \rm P \) は直線 \( \rm OG \) 上にあるので、
\( \overrightarrow{\rm OP}=k\cdot\overrightarrow{\rm OG} \) となる実数 \( k \) がある
これより、
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&k\,\left(\,\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,3\,}\overrightarrow{c}\,\right)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}k\,\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,3\,}k\,\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,3\,}k\,\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
\( \overrightarrow{a}=3\overrightarrow{\rm OM} \) であるから、\(\small [\,1\,]\) に代入すると
\(\begin{eqnarray}~~~\overrightarrow{\rm OP}&=&\displaystyle \frac{\,1\,}{\,3\,}k\cdot 3\overrightarrow{\rm OM}+\displaystyle \frac{\,1\,}{\,3\,}k\,\overrightarrow{b}+\displaystyle \frac{\,1\,}{\,3\,}k\,\overrightarrow{c}
\\[5pt]~~~&=&k\,\overrightarrow{\rm OM}+\displaystyle \frac{\,1\,}{\,3\,}k\,\overrightarrow{\rm OB}+\displaystyle \frac{\,1\,}{\,3\,}k\,\overrightarrow{\rm OC}~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
点 \( \rm P \) は平面 \( \rm MBC \) 上の点であることから、
\(\small [\,2\,]\) の係数について
\(\begin{eqnarray}~~~k+\displaystyle \frac{\,1\,}{\,3\,}k+\displaystyle \frac{\,1\,}{\,3\,}k&=&1
\\[5pt]~~~3k+k+k&=&3 \hspace{20pt}(\,∵~ {\, \small \times \,}3\,)
\\[5pt]~~~5k&=&3
\\[5pt]~~~k&=&\displaystyle \frac{\,3\,}{\,5\,}
\end{eqnarray}\)
したがって、\( \overrightarrow{\rm OP}=\displaystyle \frac{\,3\,}{\,5\,}\overrightarrow{\rm OG} \) となるので、\( \rm OP:PG=3:2 \) となる