- 数学C|空間ベクトル「四面体と2点を結ぶ線分の長さ」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|四面体と2点を結ぶ線分の長さ
空間ベクトル 36☆1辺の長さが \(1\) の正四面体 \(\rm OABC \) の辺 \(\rm OA \) の中点を \(\rm P \)、辺 \(\rm AB \) の中点を \(\rm Q \)、\( \triangle {\rm PQC} \) の重心を \(\rm G \) とするとき、線分 \(\rm OG \) の長さの求め方は?
高校数学C|空間ベクトル
解法のPoint
四面体と2点を結ぶ線分の長さ
Point:四面体と2点を結ぶ線分の長さ
① 3つの基本ベクトルを設定して、面の形が正三角形より、長さと内積の値を求める。
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とすると、
\( |\,\overrightarrow{a}\,|=|\,\overrightarrow{b}\,|=|\,\overrightarrow{c}\,|=1 \)
\( \overrightarrow{a}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{c}=\overrightarrow{c}\cdot\overrightarrow{a}=\displaystyle \frac{\,1\,}{\,2\,} \)
② 求めたい線分を3つの基本ベクトルだけで表す。
\( \overrightarrow{\rm OG}=\displaystyle \frac{\,1\,}{\,6\,}(\,2\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c}\,) \)
③ 2乗の式を展開して①を代入し、ベクトルの大きさを求める。
\( |\,\overrightarrow{\rm OG}\,|^2=\displaystyle \frac{\,1\,}{\,36\,}|\,2\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c}\,|^2 \)
これを、展開の公式
\(\begin{eqnarray}~~~&&(a+b+c)^2
\\[3pt]~~~&=&a^2+b^2+c^2+2ab+2bc+2ca\end{eqnarray}\)
を用いて展開する。
正四面体の内部の2点を結ぶ線分の長さは、
① 3つの基本ベクトルを設定して、面の形が正三角形より、長さと内積の値を求める。
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とすると、
\( |\,\overrightarrow{a}\,|=|\,\overrightarrow{b}\,|=|\,\overrightarrow{c}\,|=1 \)
\( \overrightarrow{a}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{c}=\overrightarrow{c}\cdot\overrightarrow{a}=\displaystyle \frac{\,1\,}{\,2\,} \)
② 求めたい線分を3つの基本ベクトルだけで表す。
\( \overrightarrow{\rm OG}=\displaystyle \frac{\,1\,}{\,6\,}(\,2\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c}\,) \)
③ 2乗の式を展開して①を代入し、ベクトルの大きさを求める。
\( |\,\overrightarrow{\rm OG}\,|^2=\displaystyle \frac{\,1\,}{\,36\,}|\,2\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c}\,|^2 \)
これを、展開の公式
\(\begin{eqnarray}~~~&&(a+b+c)^2
\\[3pt]~~~&=&a^2+b^2+c^2+2ab+2bc+2ca\end{eqnarray}\)
を用いて展開する。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|四面体と2点を結ぶ線分の長さ
空間ベクトル 36☆
1辺の長さが \(1\) の正四面体 \(\rm OABC \) の辺 \(\rm OA \) の中点を \(\rm P \)、辺 \(\rm AB \) の中点を \(\rm Q \)、\( \triangle {\rm PQC} \) の重心を \(\rm G \) とするとき、線分 \(\rm OG \) の長さの求め方は?
高校数学C|空間ベクトル
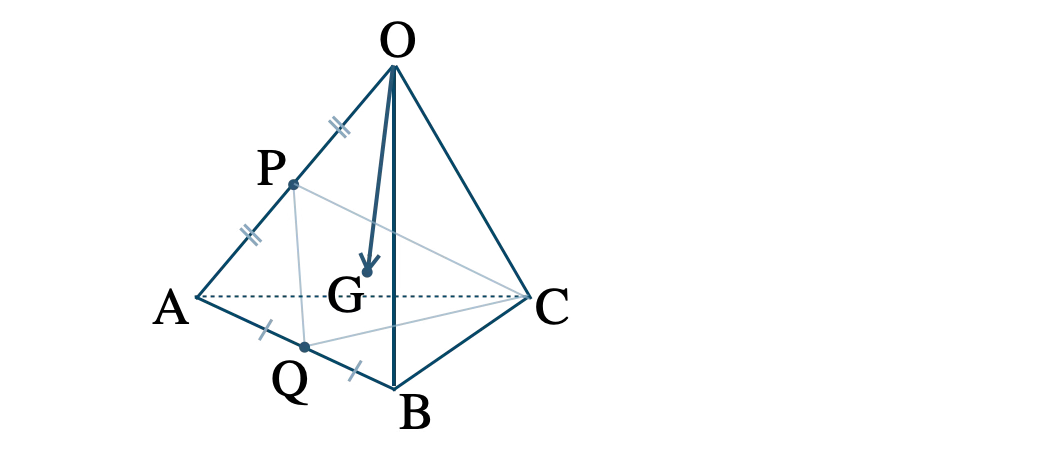
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \) とおくと、
正四面体のそれぞれの面は正三角形であることより、
\( |\,\overrightarrow{a}\,|=|\,\overrightarrow{b}\,|=|\,\overrightarrow{c}\,|=1 ~ ~ ~ \cdots {\small [\,1\,]}\)
また、正四面体より、\( \overrightarrow{a} \) と \( \overrightarrow{b} \) のなす角は \( 60^\circ \) であるので、
\(\begin{eqnarray}~~~\overrightarrow{a}\cdot\overrightarrow{b}&=&|\,\overrightarrow{a}\,|\cdot|\,\overrightarrow{b}\,|\cdot\cos 60^\circ
\\[5pt]~~~&=&1\cdot 1\cdot \displaystyle \frac{\,1\,}{\,2\,}=\displaystyle \frac{\,1\,}{\,2\,}
\end{eqnarray}\)
また、\( \overrightarrow{b}\cdot\overrightarrow{c} \) と \( \overrightarrow{c}\cdot\overrightarrow{a} \) も同様に、
\( \overrightarrow{a}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{c}=\overrightarrow{c}\cdot\overrightarrow{a}=\displaystyle \frac{\,1\,}{\,2\,} ~ ~ ~ \cdots {\small [\,2\,]}\)
次に、\( \overrightarrow{\rm OP} \) は \( {\rm OP}:{\rm PA}=1:1 \) より、
\( \overrightarrow{\rm OP}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OA}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a} \)
\( \overrightarrow{\rm OQ} \) は、\( {\rm AQ}:{\rm QB}=1:1 \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OQ}&=&\displaystyle \frac{\,\overrightarrow{\rm OA}+\overrightarrow{\rm OB}\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}
\end{eqnarray}\)
よって、\( \triangle {\rm PQC} \) の重心が \( {\rm G} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm OG}&=&\displaystyle \frac{\,\overrightarrow{\rm OP}+\overrightarrow{\rm OQ}+\overrightarrow{\rm OC}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}+\overrightarrow{c}\right)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\left(\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}+\overrightarrow{c}\right)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}\left(\displaystyle \frac{\,2\,}{\,2\,}\overrightarrow{a}+\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{b}+\displaystyle \frac{\,2\,}{\,2\,}\overrightarrow{c}\right)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,6\,}(2\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c})\end{eqnarray}\)
よって、\( |\,\overrightarrow{\rm OG}\,|^2 \) は、
\(\begin{eqnarray}~~~|\,\overrightarrow{\rm OG}\,|^2&=&\displaystyle \frac{\,1\,}{\,36\,}\cdot|\,2\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c}\,|^2
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,36\,}(2\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c})\cdot(2\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,36\,}\left\{\,4|\,\overrightarrow{a}\,|^2+|\,\overrightarrow{b}\,|^2+4|\,\overrightarrow{c}\,|^2+2\,(2\overrightarrow{a})\cdot\overrightarrow{b}+2\,\overrightarrow{b}\cdot (2\overrightarrow{c})+2\, (2\overrightarrow{c})\cdot (2\overrightarrow{a})\,\right\}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,36\,}(4|\,\overrightarrow{a}\,|^2+|\,\overrightarrow{b}\,|^2+4|\,\overrightarrow{c}\,|^2+4\overrightarrow{a}\cdot\overrightarrow{b}+4\overrightarrow{b}\cdot\overrightarrow{c}+8\overrightarrow{c}\cdot\overrightarrow{a})
\end{eqnarray}\)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,36\,}(2\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c})\cdot(2\overrightarrow{a}+\overrightarrow{b}+2\overrightarrow{c})
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,36\,}\left\{\,4|\,\overrightarrow{a}\,|^2+|\,\overrightarrow{b}\,|^2+4|\,\overrightarrow{c}\,|^2+2\,(2\overrightarrow{a})\cdot\overrightarrow{b}+2\,\overrightarrow{b}\cdot (2\overrightarrow{c})+2\, (2\overrightarrow{c})\cdot (2\overrightarrow{a})\,\right\}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,36\,}(4|\,\overrightarrow{a}\,|^2+|\,\overrightarrow{b}\,|^2+4|\,\overrightarrow{c}\,|^2+4\overrightarrow{a}\cdot\overrightarrow{b}+4\overrightarrow{b}\cdot\overrightarrow{c}+8\overrightarrow{c}\cdot\overrightarrow{a})
\end{eqnarray}\)
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) より、
\(\begin{eqnarray}\hspace{28pt}~~~&=&\displaystyle \frac{\,1\,}{\,36\,}\left(4\cdot 1^2+1^2+4\cdot 1^2+4\cdot \displaystyle \frac{\,1\,}{\,2\,}+4\cdot \displaystyle \frac{\,1\,}{\,2\,}+8\cdot \displaystyle \frac{\,1\,}{\,2\,}\right)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,36\,}\left(4+1+4+2+2+4\right)
\\[5pt]~~~&=&\displaystyle \frac{\,17\,}{\,36\,}\end{eqnarray}\)
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,36\,}\left(4+1+4+2+2+4\right)
\\[5pt]~~~&=&\displaystyle \frac{\,17\,}{\,36\,}\end{eqnarray}\)
※ 数式は横にスクロールできます。
したがって、\( |\,\overrightarrow{\rm OG}\,|=\displaystyle \frac{\,\sqrt{17}\,}{\,6\,} \) となる



