- 数学C|空間ベクトル「座標空間の2点の内分点・外分点・中点」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|座標空間の2点の内分点・外分点・中点
空間ベクトル 38座標空間の2点 \( {\rm A}(1~,~ 2~,~ 3)~,~\)\( {\rm B}(4~,~ -1~,~ 2) \) に対して、線分 \(\rm AB \) の \( 2:3 \) の内分点、\( 2:3 \) の外分点、中点の座標の求め方は?
高校数学C|空間ベクトル
解法のPoint
座標空間の2点の内分点・外分点・中点
Point:座標空間の2点の内分点・外分点・中点
\({\small [\,1\,]}\) \( m:n \) の内分点 \( {\rm P} \) は、
\( x \) 座標は \( x=\displaystyle\frac{\,nx_1+mx_2\,}{\,m+n\,} \)
\( y \) 座標は \( y=\displaystyle\frac{\,ny_1+my_2\,}{\,m+n\,} \)
\( z \) 座標は \( z=\displaystyle\frac{\,nz_1+mz_2\,}{\,m+n\,} \)
\({\small [\,2\,]}\) \( m:n \) の外分点 \( {\rm Q} \) は、
\( x \) 座標は \( x=\displaystyle\frac{\,-nx_1+mx_2\,}{\,m-n\,} \)
\( y \) 座標は \( y=\displaystyle\frac{\,-ny_1+my_2\,}{\,m-n\,} \)
\( z \) 座標は \( z=\displaystyle\frac{\,-nz_1+mz_2\,}{\,m-n\,} \)
※ 内分点の式の比のどちらかにマイナスを付けて、\(m:-n\) と考える。
\({\small [\,3\,]}\) 中点 \( {\rm M} \) は、
\( x \) 座標は \( x=\displaystyle\frac{\,x_1+x_2\,}{\,2\,} \)
\( y \) 座標は \( y=\displaystyle\frac{\,y_1+y_2\,}{\,2\,} \)
\( z \) 座標は \( z=\displaystyle\frac{\,z_1+z_2\,}{\,2\,} \)
座標空間の2点 \( {\rm A}(x_1~,~y_1~,~z_1)~,~\)\({\rm B}(x_2~,~y_2~,~z_2) \) と線分 \( {\rm AB} \) の
\({\small [\,1\,]}\) \( m:n \) の内分点 \( {\rm P} \) は、
\( x \) 座標は \( x=\displaystyle\frac{\,nx_1+mx_2\,}{\,m+n\,} \)
\( y \) 座標は \( y=\displaystyle\frac{\,ny_1+my_2\,}{\,m+n\,} \)
\( z \) 座標は \( z=\displaystyle\frac{\,nz_1+mz_2\,}{\,m+n\,} \)
\({\small [\,2\,]}\) \( m:n \) の外分点 \( {\rm Q} \) は、
\( x \) 座標は \( x=\displaystyle\frac{\,-nx_1+mx_2\,}{\,m-n\,} \)
\( y \) 座標は \( y=\displaystyle\frac{\,-ny_1+my_2\,}{\,m-n\,} \)
\( z \) 座標は \( z=\displaystyle\frac{\,-nz_1+mz_2\,}{\,m-n\,} \)
※ 内分点の式の比のどちらかにマイナスを付けて、\(m:-n\) と考える。
\({\small [\,3\,]}\) 中点 \( {\rm M} \) は、
\( x \) 座標は \( x=\displaystyle\frac{\,x_1+x_2\,}{\,2\,} \)
\( y \) 座標は \( y=\displaystyle\frac{\,y_1+y_2\,}{\,2\,} \)
\( z \) 座標は \( z=\displaystyle\frac{\,z_1+z_2\,}{\,2\,} \)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|座標空間の2点の内分点・外分点・中点
空間ベクトル 38
座標空間の2点 \( {\rm A}(1~,~ 2~,~ 3)~,~\)\( {\rm B}(4~,~ -1~,~ 2) \) に対して、線分 \(\rm AB \) の \( 2:3 \) の内分点、\( 2:3 \) の外分点、中点の座標の求め方は?
高校数学C|空間ベクトル
線分 \( {\rm AB} \) の \( 2:3 \) の内分点 \( {\rm P} \) は、
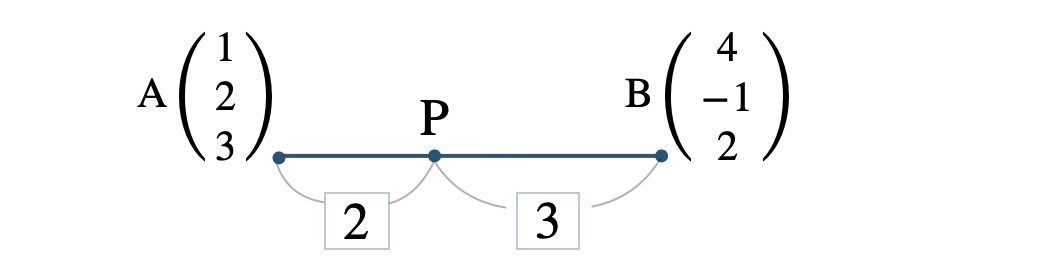

\( x \) 座標は、
\(\begin{eqnarray}~~~&=&\displaystyle\frac{\,3\cdot 1+2\cdot 4\,}{\,2+3\,}
\\[5pt]~~~&=&\displaystyle\frac{\,3+8\,}{\,5\,}=\displaystyle\frac{\,11\,}{\,5\,}\end{eqnarray}\)
\( y \) 座標は、
\(\begin{eqnarray}~~~&=&\displaystyle\frac{\,3\cdot 2+2\cdot (-1)\,}{\,2+3\,}
\\[5pt]~~~&=&\displaystyle\frac{\,6-2\,}{\,5\,}=\displaystyle\frac{\,4\,}{\,5\,}\end{eqnarray}\)
\( z \) 座標は、
\(\begin{eqnarray}~~~&=&\displaystyle\frac{\,3\cdot 3+2\cdot 2\,}{\,2+3\,}
\\[5pt]~~~&=&\displaystyle\frac{\,9+4\,}{\,5\,}=\displaystyle\frac{\,13\,}{\,5\,}\end{eqnarray}\)
したがって、\( {\rm P}\left(\,\displaystyle\frac{\,11\,}{\,5\,}~,~\displaystyle\frac{\,4\,}{\,5\,}~,~\displaystyle\frac{\,13\,}{\,5\,}\,\right) \)
線分 \( {\rm AB} \) の \( 2:3 \) の外分点 \( {\rm Q} \) は、
以下の図は実際にはありえない図となっているが、計算する上では、内分点と同じように考えて、比のどちらか一方にマイナスを付ける。

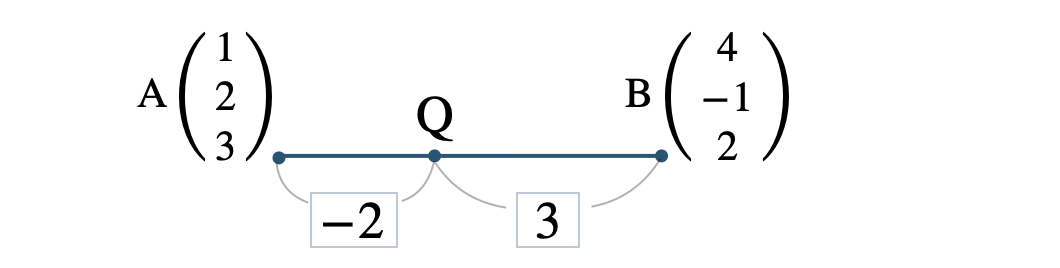


\( x \) 座標は、
\(\begin{eqnarray}~~~&=&\displaystyle\frac{\,3\cdot 1+(-2)\cdot 4\,}{\,(-2)+3\,}
\\[5pt]~~~&=&3-8=-5\end{eqnarray}\)
\( y \) 座標は、
\(\begin{eqnarray}~~~&=&\displaystyle\frac{\,3\cdot 2+(-2)\cdot (-1)\,}{\,(-2)+3\,}
\\[5pt]~~~&=&6+2=8\end{eqnarray}\)
\( z \) 座標は、
\(\begin{eqnarray}~~~&=&\displaystyle\frac{\,3\cdot 3+(-2)\cdot 2\,}{\,(-2)+3\,}
\\[5pt]~~~&=&9-4=5\end{eqnarray}\)
したがって、\( {\rm Q}(-5~,~8~,~5) \)
線分 \( {\rm AB} \) の中点 \( {\rm M} \) は、
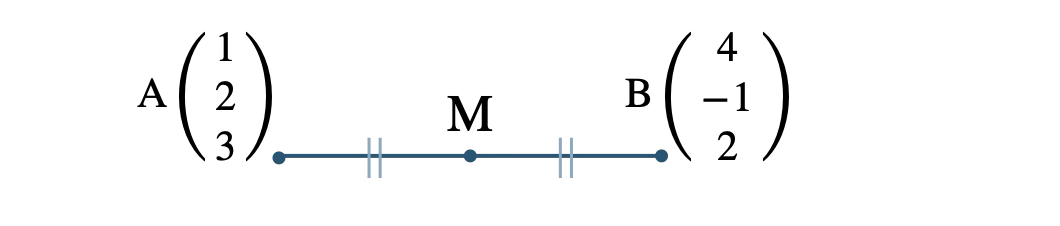

\( x \) 座標は、
\(\begin{eqnarray}~~~x&=&\displaystyle\frac{\,1+4\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle\frac{\,5\,}{\,2\,}\end{eqnarray}\)
\( y \) 座標は、
\(\begin{eqnarray}~~~y&=&\displaystyle\frac{\,2+(-1)\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle\frac{\,1\,}{\,2\,}\end{eqnarray}\)
\( z \) 座標は、
\(\begin{eqnarray}~~~z&=&\displaystyle\frac{\,3+2\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle\frac{\,5\,}{\,2\,}\end{eqnarray}\)
したがって、\( {\rm M}\left(\,\displaystyle\frac{\,5\,}{\,2\,}~,~\displaystyle\frac{\,1\,}{\,2\,}~,~\displaystyle\frac{\,5\,}{\,2\,}\,\right) \)



