- 数学C|空間ベクトル「座標空間の点を通る平面の方程式」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|座標空間の点を通る平面の方程式
空間ベクトル 40座標空間の点 \( {\rm A}(1~,~ 2~,~ 3) \) を通り、\( x \) 軸に垂直、\( y \) 軸に垂直、\( z \) 軸に垂直、\( xy \) 平面に平行、\( yz \) 平面に平行、\( zx \) 平面に平行な平面の方程式の求め方は?また、平面 \(y=1\) に関して点 \({\rm A}\) と対称な点 \({\rm B}\) の座標や、平面 \(z=1\) に関して点 \({\rm A}\) と対称な点 \({\rm C}\) の座標の求め方は?
高校数学C|空間ベクトル
解法のPoint
座標空間の点を通る平面の方程式
Point:座標空間の点を通る平面の方程式

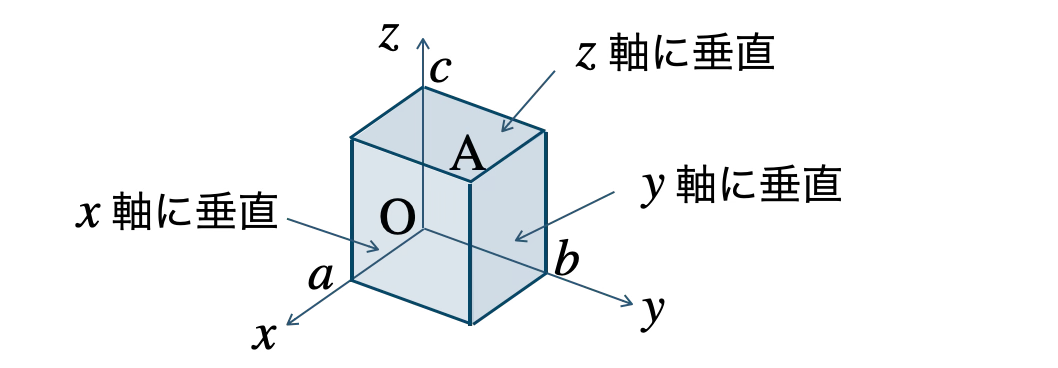
点 \( {\rm A}(a~,~b~,~c) \) を通り、
\( x \) 軸に垂直な平面の方程式は、\( x=a \)
\( y \) 軸に垂直な平面の方程式は、\( y=b \)
\( z \) 軸に垂直な平面の方程式は、\( z=c \)

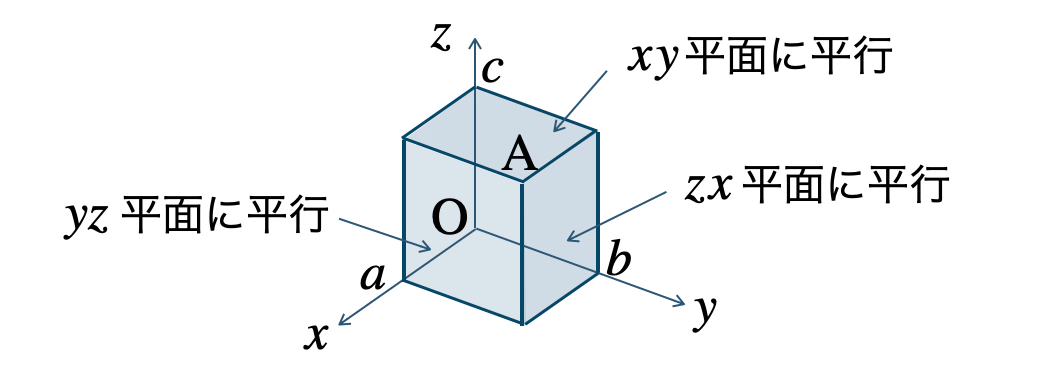
\( xy \) 平面に平行な平面の方程式は、\( z=c \)
\( yz \) 平面に平行な平面の方程式は、\( x=a \)
\( zx \) 平面に平行な平面の方程式は、\( y=b \)
平面 \( x=2 \) に関して、点 \( {\rm A}(1~,~2~,~3) \) と対称な点 \( {\rm P} \) は、

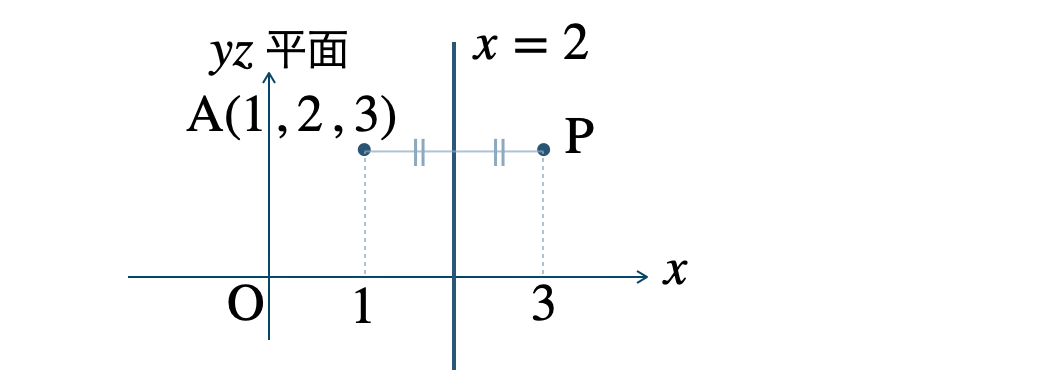
よって、点 \( {\rm P}(3~,~2~,~3) \) となる
■ 軸に垂直な平面の方程式


点 \( {\rm A}(a~,~b~,~c) \) を通り、
\( x \) 軸に垂直な平面の方程式は、\( x=a \)
\( y \) 軸に垂直な平面の方程式は、\( y=b \)
\( z \) 軸に垂直な平面の方程式は、\( z=c \)
■ 平面に平行な平面の方程式


\( xy \) 平面に平行な平面の方程式は、\( z=c \)
\( yz \) 平面に平行な平面の方程式は、\( x=a \)
\( zx \) 平面に平行な平面の方程式は、\( y=b \)
■ 平面に関して点と対称な点の座標
平面 \( x=2 \) に関して、点 \( {\rm A}(1~,~2~,~3) \) と対称な点 \( {\rm P} \) は、


よって、点 \( {\rm P}(3~,~2~,~3) \) となる
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|座標空間の点を通る平面の方程式
空間ベクトル 40
座標空間の点 \( {\rm A}(1~,~ 2~,~ 3) \) を通り、\( x \) 軸に垂直、\( y \) 軸に垂直、\( z \) 軸に垂直、\( xy \) 平面に平行、\( yz \) 平面に平行、\( zx \) 平面に平行な平面の方程式の求め方は?また、平面 \(y=1\) に関して点 \({\rm A}\) と対称な点 \({\rm B}\) の座標や、平面 \(z=1\) に関して点 \({\rm A}\) と対称な点 \({\rm C}\) の座標の求め方は?
高校数学C|空間ベクトル
点 \( {\rm A}(1~,~2~,~3) \) を通り、
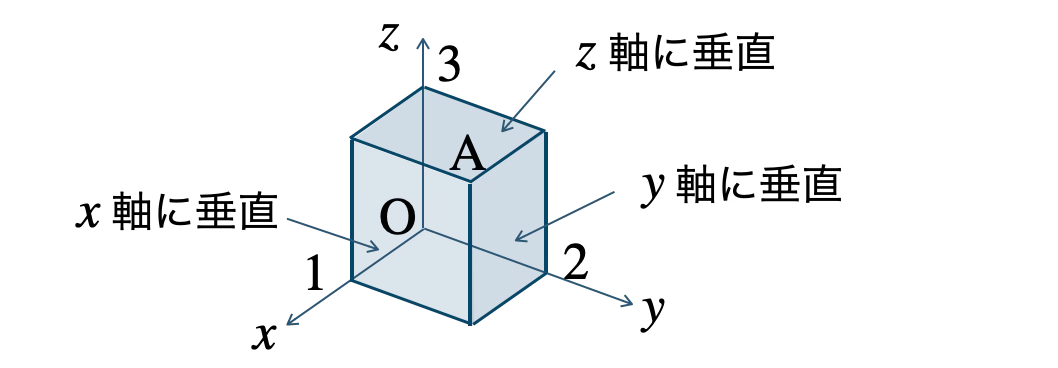

\( x \) 軸に垂直な平面の方程式は、\( x=1 \)
\( y \) 軸に垂直な平面の方程式は、\( y=2 \)
\( z \) 軸に垂直な平面の方程式は、\( z=3 \)
点 \( {\rm A}(1~,~2~,~3) \) を通り、
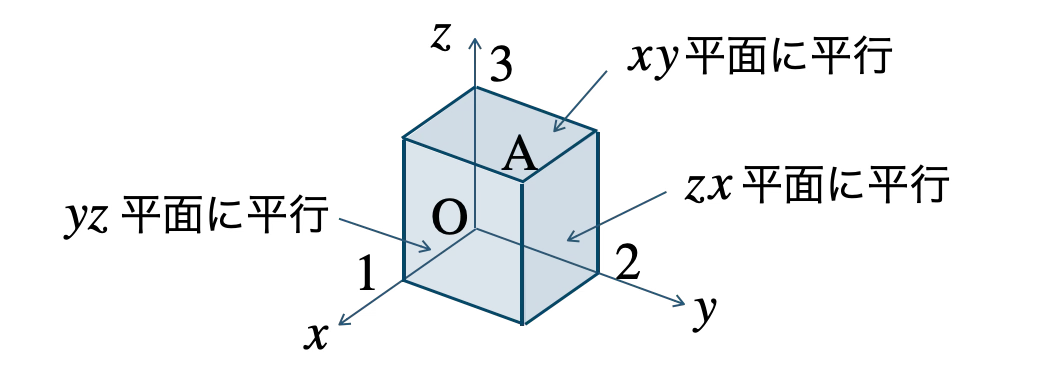

\( xy \) 平面に平行な平面の方程式は、\( z=3 \)
\( yz \) 平面に平行な平面の方程式は、\( x=1 \)
\( zx \) 平面に平行な平面の方程式は、\( y=2 \)
平面 \( y=1 \) に関して、点 \( {\rm A}(1~,~2~,~3) \) と対称な点 \( {\rm B} \) は、
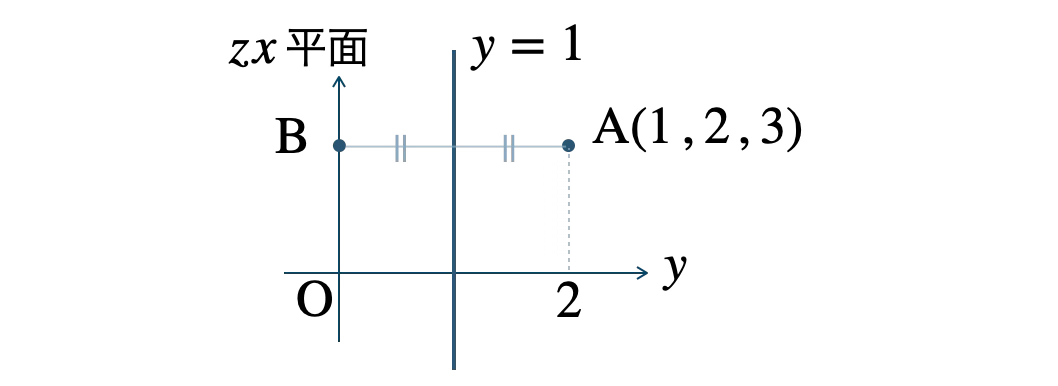

よって、点 \( {\rm B}(1~,~0~,~3) \) となる
平面 \( z=1 \) に関して、点 \( {\rm A}(1~,~2~,~3) \) と対称な点 \( {\rm C} \) は、
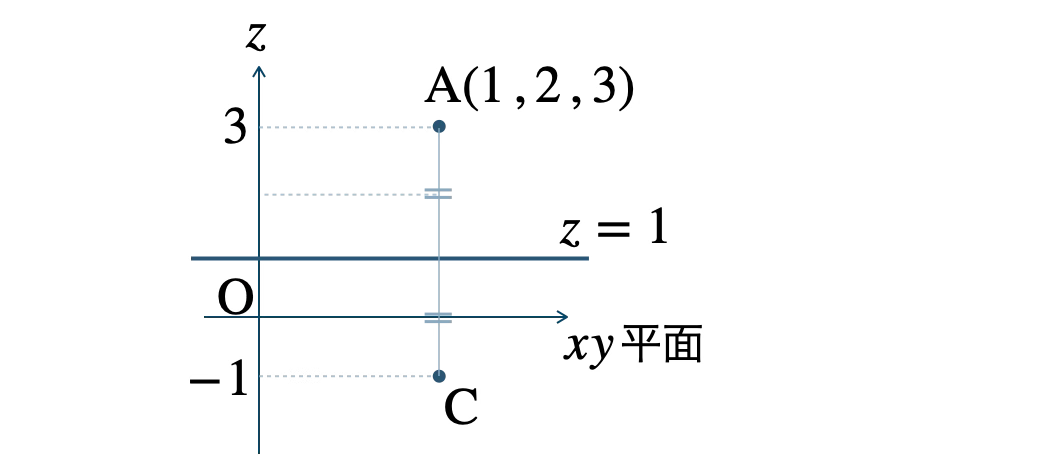

よって、点 \( {\rm C}(1~,~2~,~-1) \) となる



