【新課程】数研出版：数学Ｂ[710]

p.55 練習1

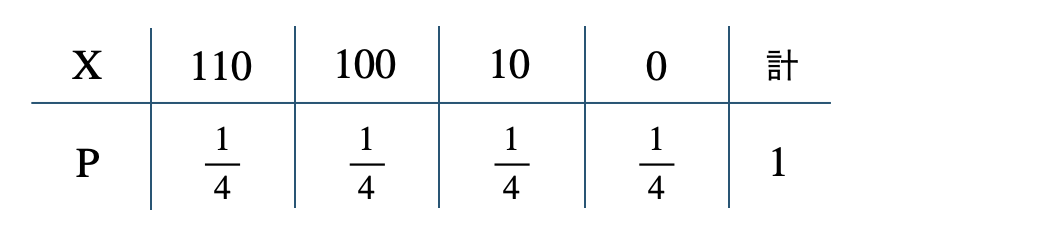
p.57 練習2$$~~~3$$

p.57 練習3$$~~~\frac{\,7\,}{\,5\,}$$

p.59 練習4$$~~~V(X)=\frac{\,9\,}{\,25\,}~,~\sigma (X)=\frac{\,3\,}{\,5\,}$$

p.60 練習5$$~~~V(X)=\frac{\,9\,}{\,25\,}~,~\sigma (X)=\frac{\,3\,}{\,5\,}$$

p.60 深める標準偏差 \(\sigma (X)\) の値が小さいと、分散 \(V(X)\) の値も小さくなる
また、分散の定義より、確率変数と期待値との差 \(\{x_k-m\}\) が小さくなるので確率変数 \(X\) のとる値は分布の平均の近くに集中する

p.62 練習6$${\small (1)}~E(Y)=\frac{\,9\,}{\,2\,}~,~V(Y)=\frac{\,35\,}{\,12\,}$$$$~~~~,~\sigma(Y)=\frac{\,\sqrt{105}\,}{\,6\,}$$$${\small (2)}~E(Y)=-7~,~V(Y)=\frac{\,35\,}{\,3\,}$$$$~~~~,~\sigma(Y)=\frac{\,\sqrt{105}\,}{\,3\,}$$$${\small (3)}~E(Y)=\frac{\,17\,}{\,2\,}~,~V(Y)=\frac{\,105\,}{\,4\,}$$$$~~~~,~\sigma(Y)=\frac{\,\sqrt{105}\,}{\,2\,}$$

p.64 練習7

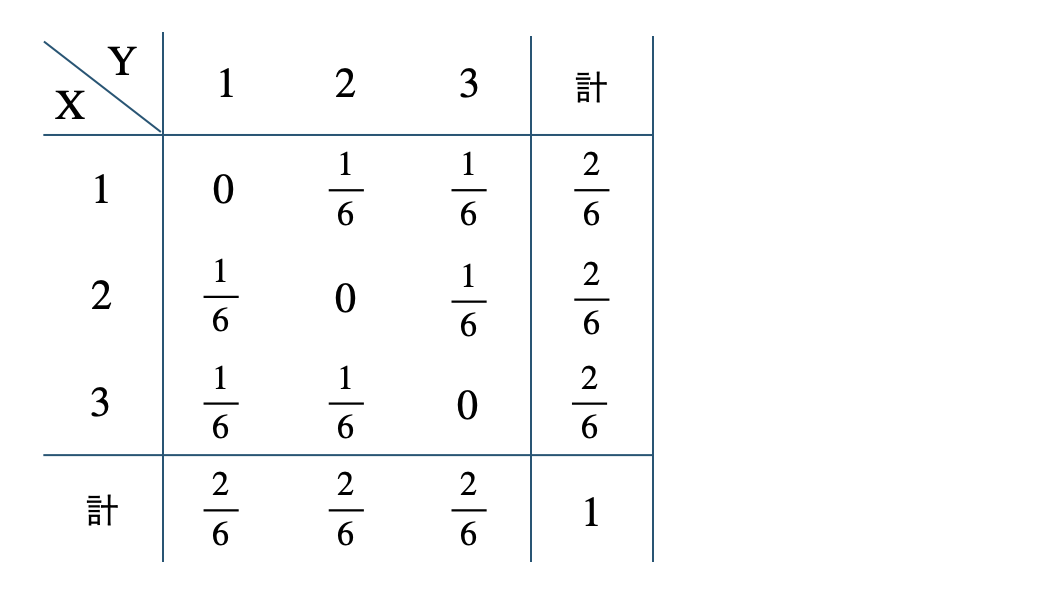
p.66 練習8$$~~~16$$

p.66 問1$$~~~7$$

p.66 練習9$$~~~\frac{\,53\,}{\,2\,}$$

p.66 問2$$~~~\frac{\,21\,}{\,2\,}$$

p.66 練習10$$~~~80$$

p.67 問3\(a=1~,~b=1\) のときは例5より成り立つ
\(a=0~,~2\) のとき、$$~~~P(X=a)=\frac{\,4\,}{\,16\,}=\frac{\,1\,}{\,4\,}$$\(b=0~,~2\) のとき、$$~~~P(X=b)=\frac{\,4\,}{\,16\,}=\frac{\,1\,}{\,4\,}$$
また、\(a=1\) と \(b=0~,~2\) の任意の組合せで、$$~~~P(X=a)=\frac{\,8\,}{\,16\,}=\frac{\,1\,}{\,2\,}$$$$~~~P(Y=b)=\frac{\,4\,}{\,16\,}=\frac{\,1\,}{\,4\,}$$$$~~~P(X=a~,~Y=b)=\frac{\,2\,}{\,16\,}=\frac{\,1\,}{\,8\,}$$\(a=0~,~2\) と \(b=1\) の任意の組合せで、$$~~~P(X=a)=\frac{\,4\,}{\,16\,}=\frac{\,1\,}{\,4\,}$$$$~~~P(Y=b)=\frac{\,8\,}{\,16\,}=\frac{\,1\,}{\,2\,}$$$$~~~P(X=a~,~Y=b)=\frac{\,2\,}{\,16\,}=\frac{\,1\,}{\,8\,}$$
したがって、\(X\) のとる任意の値 \(a\) と \(Y\) のとる任意の値 \(b\) について、$$~~~P(X=a~,~Y=b)=P(X=a)P(Y=b)$$が成り立つ

p.66 練習11\(X~,~Y\) の同時分布は、次のようになる

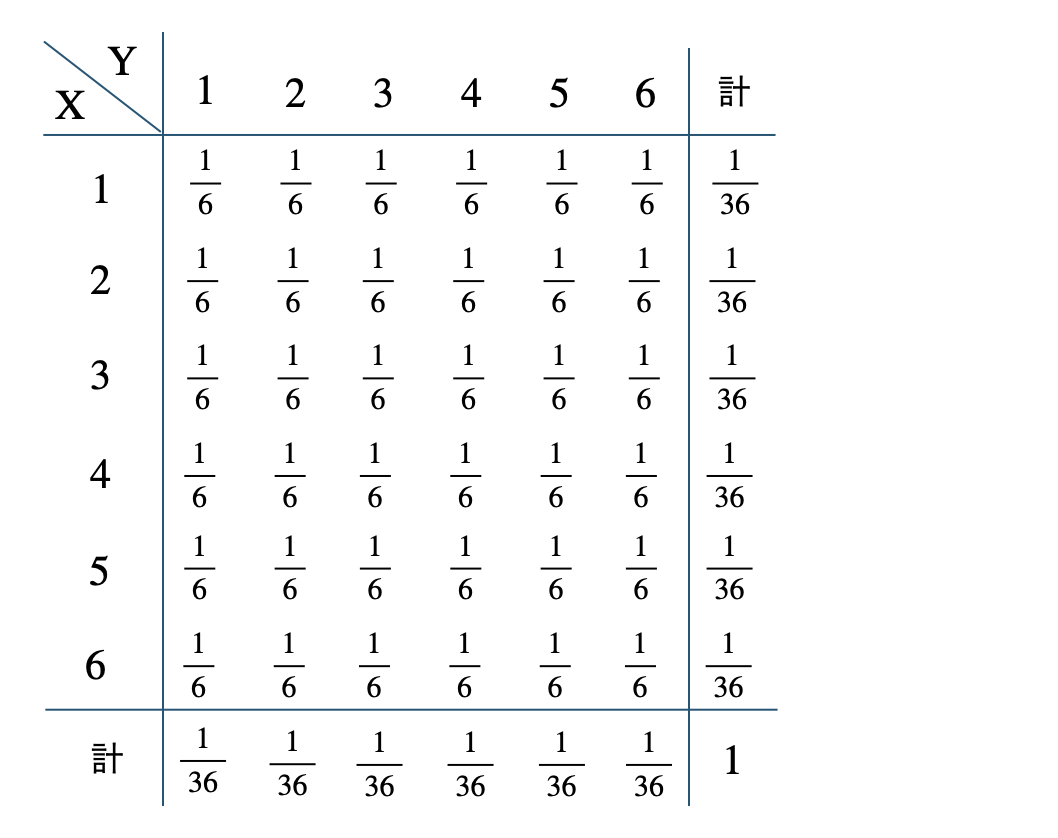
これより、\(a=1\) 〜 \(6\) と \(b=1\) 〜 \(6\) の任意の組合せについて、$$~~~P(X=a)=\frac{\,1\,}{\,6\,}~,~P(Y=b)=\frac{\,1\,}{\,6\,}$$$$~~~P(X=a~,~Y=b)=\frac{\,1\,}{\,36\,}$$であるから、$$~~~P(X=a~,~Y=b)=P(X=a)P(Y=b)$$が成り立つ

p.71 練習12$$~~~P(B)=\frac{\,1\,}{\,6\,}~,~P(C)=\frac{\,5\,}{\,36\,}$$$$~~~P(B\cap C)=\frac{\,1\,}{\,36\,}$$これより、２つの事象 \(B\) と \(C\) は従属である

p.72 練習13$$~~~4$$

p.73 練習14$$~~~\frac{\,343\,}{\,8\,}$$

p.73 練習15　期待値 \(-1\)、分散 \(9\)、標準偏差 \(3\)

p.74 練習16　分散 \(24\)、標準偏差 \(2\sqrt{6}\)

p.74 練習17$$~~~\frac{\,35\,}{\,4\,}$$

p.77 練習18$${\small (1)}~E(X)=3~,~V(X)=\frac{\,9\,}{\,4\,}~,~\sigma(X)=\frac{\,3\,}{\,2\,}$$$${\small (2)}~E(X)=\frac{\,9\,}{\,2\,}~,~V(X)=\frac{\,9\,}{\,4\,}~,~\sigma(X)=\frac{\,3\,}{\,2\,}$$$${\small (3)}~E(X)=\frac{\,16\,}{\,3\,}~,~V(X)=\frac{\,16\,}{\,9\,}$$$$~~~~,~\sigma(X)=\frac{\,4\,}{\,3\,}$$

p.77 練習19$${\small (1)}~B\left(10~,~\frac{\,1\,}{\,2\,}\right)~,~E(X)=5$$$$~~~~,~\sigma(X)=\frac{\,\sqrt{10}\,}{\,2\,}$$$${\small (2)}~B\left(50~,~\frac{\,3\,}{\,100\,}\right)~,~E(X)=\frac{\,3\,}{\,2\,}$$$$~~~~,~\sigma(X)=\frac{\,\sqrt{582}\,}{\,20\,}$$

p.80 練習20$${\small (1)}~P(0≦X≦1)=0.2$$$$~~~~,~P(1≦X≦3)=0.4$$$${\small (2)}~P(0≦X≦1)=\frac{\,1\,}{\,4\,}$$$$~~~~,~P(1≦X≦2)=\frac{\,3\,}{\,4\,}$$

p.80 問4$$~~~E(X)=\frac{\,2\,}{\,3\,}~,~V(X)=\frac{\,1\,}{\,18\,}$$$$~~~~,~\sigma(X)=\frac{\,\sqrt{2}\,}{\,6\,}$$

p.80 練習21$${\small (1)}~E(X)=\frac{\,5\,}{\,2\,}~,~V(X)=\frac{\,25\,}{\,12\,}$$$$~~~~,~\sigma(X)=\frac{\,5\sqrt{3}\,}{\,6\,}$$$${\small (2)}~E(X)=\frac{\,4\,}{\,3\,}~,~V(X)=\frac{\,2\,}{\,9\,}$$$$~~~~,~\sigma(X)=\frac{\,\sqrt{2}\,}{\,3\,}$$

p.83 練習22$${\small (1)}~0.8413$$$${\small (2)}~0.3085$$$${\small (3)}~0.1359$$$${\small (4)}~0.6826$$$${\small (5)}~0.9544$$$${\small (6)}~0.9973$$

p.83 練習23$${\small (1)}~0.9544$$$${\small (2)}~0.6554$$$${\small (3)}~0.3811$$

p.84 問5$${\small (1)}~u=0.84$$\({\small (2)}~\)\(175~{\rm cm}\) 以上

p.84 練習24\({\small (1)}~\)約 \(9\) %
\({\small (2)}~\)約 \(42\) %
\({\small (3)}~\)\(148~{\rm cm}\) 以下

p.86 練習25$$~~~0.4772$$

p.90 練習26

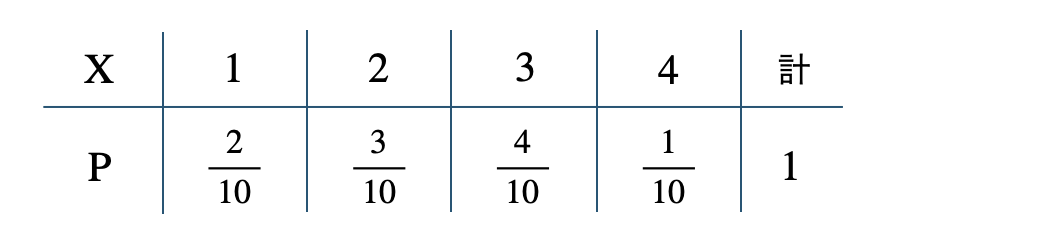
母平均は \({\large \frac{\,12\,}{\,5\,}}\)、母標準偏差は \({\large \frac{\,\sqrt{21}\,}{\,5\,}}\)

p.91 問6\({\small (1)}~\)

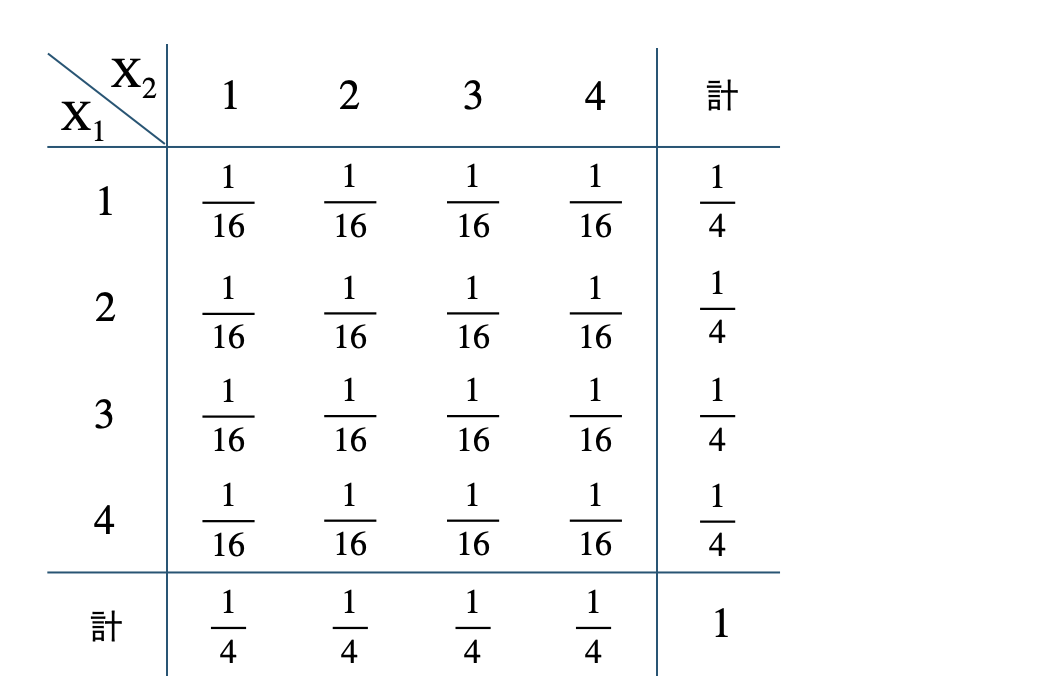
\({\small (2)}~\)

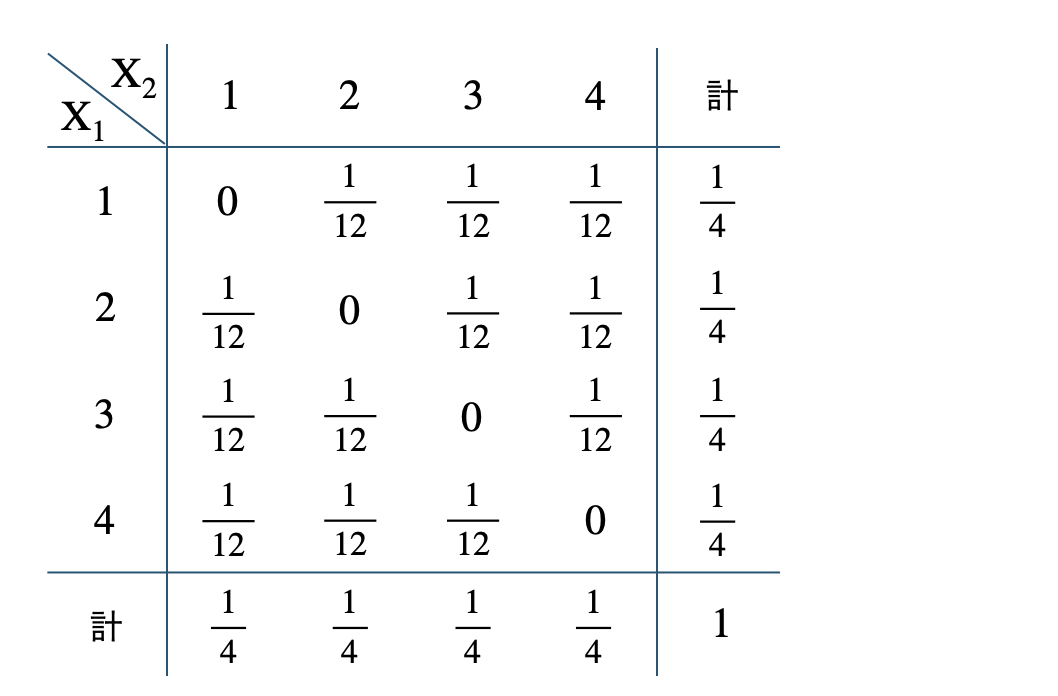
p.93 問7\({\small (1)}~\)

\({\small (2)}~\)

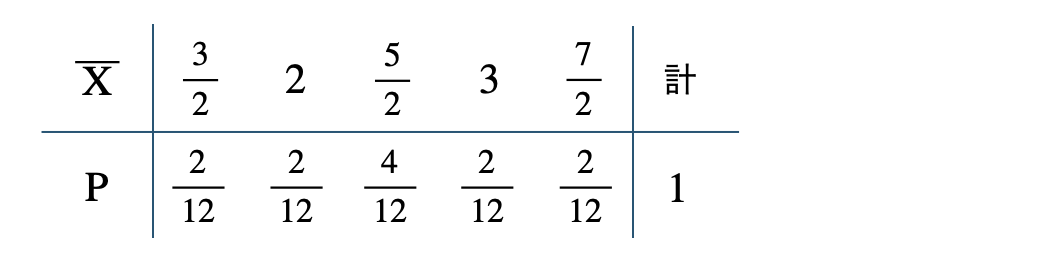
p.94 練習27　期待値 \(64.1~{\rm kg}\)、標準偏差 \(1.05~{\rm kg}\)

p.95 練習28　期待値 \({\large \frac{\,1\,}{\,10\,}}\)、標準偏差 \({\large \frac{\,3\,}{\,10\sqrt{n}\,}}\)

p.97 練習29$$~~~0.1587$$

p.98 問8$$~~~0.6826$$

p.98 練習30\(n=400\) のとき、\(0.9544\)
\(n=900\) のとき、\(0.9973\)

p.101 練習31$$~~~[105.2~,~105.6]$$ただし、単位は \({\rm cm}\)

p.101 練習32$$~~~[31.9~,~33.1]$$ただし、単位は \({\rm mg}\)

p.103 練習33$$~~~[0.467~,~0.533]$$

p.106 練習34\(1\) の目が出る確率が \({\large \frac{\,1\,}{\,6\,}}\) ではないと判断できない

p.107 練習35品種改良によって発芽率が上がったと判断できない

p.108 練習36１缶あたりの内容量は表示通りでないと判断できない